西瓜书第三章习题及答案

笔记：
线性模型（Linear model）：试图学习一个通过属性的线性组合来进行预测的函数。
线性回归（Linear regression）：试图学习一个线性模型以尽可能准确地预测实值输出标记。

式子(3.2)如图所示：

想法实录：想着如果是一个模型预测的刚刚好与真实值一致，那还需要偏置项吗？
事实证明我想想的是什么？？？ 想的太简单了！
看到这个题目，要知道偏置项它有什么作用? 为什么需要偏置项? 参考文章。其实它的大致意思就是说偏置项能够让我们的模型更好地拟合真实值。

解答：
我们都知道线性模型y = ax + b， a表示的是直线与X轴的偏移角度，b则表示在Y轴上的截距。我们知道偏置量在拟合中的至关重要，因此b是必须存在的，它体现模型整体上的浮动，可以根据具体情况对偏差进行修正。针对本题，个人觉得以下两点相对来说比较合理点。
①在f(x)进行归一化处理时消除偏置，归一化详解参考。
②当只需要考虑x的取值对y的影响的话，则可以不用考虑b。
3.1、3.2、3.3、3.5参考链接

数据集：（直接复制新建txt文件，需要注意数字之间是tab键隔开的，代码中用的是：watermelon_30a.txt）
（三列的含义分别是：密度,含糖率,好瓜（1代表正例-好瓜，0代表反例-不是好瓜））

0.697 0.46 1
0.774 0.376 1
0.634 0.264 1
0.608 0.318 1
0.556 0.215 1
0.403 0.237 1
0.481 0.149 1
0.437 0.211 1
0.666 0.091 0
0.243 0.267 0
0.245 0.057 0
0.343 0.099 0
0.639 0.161 0
0.657 0.198 0
0.36 0.37 0
0.593 0.042 0
0.719 0.103 0
首先需要构造一个阶跃函数我们使用sigmoid函数，常用的有(1)y = $\frac{1}{1+e^{-x}}$；(2)y = $\frac{2}{1+e^{-2x}}$，本文代码使用第一个函数。
代码如下：

'''西瓜书第三章课后题3.3'''
#导入需要的库
#梯度上升法
from numpy import *
import operator
from os import listdir

#根据数学公式定义sigmoid函数
def sigmoid(inX):
    return 1.0/(1+exp(-inX))

#加载数据函数
def loadDataSet():
    dataMat=[];labelMat=[]
    fr=open(r'F:\\python\\dataset\\chater3\\watermelon_30a.txt')
    #fr=open(r'F:\\python\\dataset\\chater3\\testSet.txt')
    for line in fr.readlines():
        lineArr=line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])#[1.0,属性值1，属性值2 
        labelMat.append(int(lineArr[2]))#类别标签
    return dataMat,labelMat

#梯度上升算法--核心算法

def gradAscent(dataMat, classLabels):
    dataMatrix = mat(dataMat)#转为NumPy可识别的矩阵
    labelMat = mat(classLabels).transpose()#为了便于计算，classLabels为行向量转为列向量
    m,n = shape(dataMatrix)#获取输入数据的条数m，特征数n
    alpha = 0.001 #设定迭代的步长alpha
    maxCycles = 500 #设置循环次数500次，即训练次数
    weights = ones((n, 1))  #权值初始化为1，后面根据样本数据调整、训练结束得到最优权值、weights为n行，1维。为列向量。
    for k in range(maxCycles):   #循环maxCycles次，每次根据模型输出结果与真实值的误差，调整权值
        #dataMatrix*weights矩阵的乘法。
        #事实上包含300次的乘积
        #h为模型给出的一个预测值
        h = sigmoid(dataMatrix * weights)  
        error = labelMat - h #计算误差，每条记录真实值与预测值之差
        weights = weights + alpha * dataMatrix.transpose() * error    #循环次数结束，返回回归系数
    return weights

#画出决策边界

def plotBestFit(weights):
    import matplotlib.pyplot as plt 
    dataMat,labelMat=loaddata()
    dataArr=array(dataMat)
    n=shape(dataArr)[0]
    xcord1=[];ycord1=[]
    xcord2=[];ycord2=[]
    for i in range(n):
        if int(labelMat[i])==1:
            xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    x=arange(0.0,1.0,0.1)
    y=(-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('x1');plt.ylabel('x2')
    plt.show()  #画出的是X1与X2的关系图，横坐标X1，纵坐标X2

dataArr,labelMat = loadDataSet() #调用函数loaDdataSet
print(dataArr)

print(labelMat)
print("--------------------华丽分隔符-----------------------")
weights = gradAscent(dataArr,labelMat) #调用函数gradAscent
print('求出的权重：{}'.format(weights)) #pyhton格式化输出
print(plotBestFit(weights.getA()))  #getA()方法的使用

结果展示：
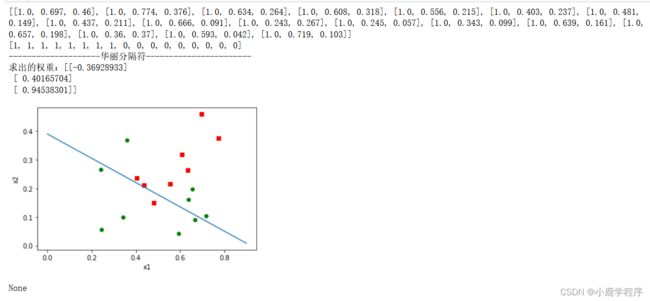备注：getA()函数与mat()函数作用相反，mat()是将数组转换成numpy矩阵，而getA()则是将numpy矩阵转化成数组形式，getA()用法参考。
3.3参考书籍：《机器学习实战》 [美] Peter Harrington —第五章内容