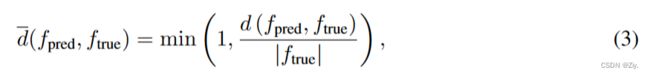【2022】Rethinking Symbolic Regression Datasets and Benchmarks for Scientific Discovery

单纯地机翻内容

Abstract

本文重新审视了符号回归的数据集和评价标准，符号回归是一项从给定数据中恢复数学表达式的任务，特别关注其在科学发现方面的潜力。以现有的基于Feynman物理学讲座的数据集所使用的一组公式为重点，我们重新创建了120个数据集来讨论科学发现的符号回归（SRSD）的性能。对于这120个SRSD数据集中的每一个，我们都仔细审查了公式及其变量的属性，以设计合理的现实的取样范围，这样我们新的SRSD数据集就可以用来评估SRSD的潜力，例如SR方法是否能从这些数据集中（重新）发现物理规律。作为一个评估指标，我们还提出使用预测方程和ground-truth方程树之间的归一化编辑距离。现有的指标要么是二进制，要么是目标值和SR模型对给定输入的预测值之间的误差，而归一化的编辑距离则是评估ground-truth和预测方程树之间的某种相似性。我们在SRBench中使用五个最先进的SR方法和一个基于Transformer架构的简单基线方法（Symbolic Transformer），在我们新的SRSD数据集上进行了实验。结果表明，我们提供了一个更真实的性能评估，并为科学发现开辟了一个新的基于机器学习的方法。我们的数据集1 2 3和代码库4是公开可用的。

Introduction

使用像ML和DL这种黑箱模型对于非ML专家来说比较难理解。符号回归（SR）的任务是生成拟合给定数据集的数学表达式（符号表达式）。SR已经在遗传编程（GP）界得到了研究，而基于DL的SR已经从ML/DL界吸引了更多的关注。不同领域的研究者将SR应用于自己的领域，例如物理，应用机械学，气候学，材料学和化学。

SRBench，统一的符号回归方法的基准框架。在这一benchmark的研究中，他们整合了Feynman Symbolic Regression Database (FSRD)和ODE-Strogatz repository，通过使用使用大规模异构计算集群，来和许多的SR方法进行对比。

为了讨论科学发现的符号回归（symbolic regression for scientific discovery ，SRSD）的潜力，仍有一些问题需要解决：过度简化的数据集和缺乏对SRSD的评价指标。对于符号回归任务，现有的数据集包括从有限的领域（如1到5的范围）取样的值，而且没有有着合理现实价值的大规模数据集来捕捉公式及其变量的属性。因此，很难用这种现有的数据集讨论符号回归在科学发现方面的潜力。例如，FSRD由120个公式组成，这些公式主要选自Feynman Lectures Series6[10-12]，是SRBench[26]中使用的核心基准数据集。虽然这些公式表明了物理规律，但每个数据集中使用的变量和常数没有物理意义，因为这些数据集不是为了从现实世界的观测数据中发现物理规律。(见第3.1节）。

此外，目前还缺乏适当的指标来评估这些SRSD的方法。一个直观的方法是测量预测误差或预测值与测试数据中的目标值之间的相关性，就像在标准回归问题中一样。然而，**即使是与原始规律不同的复杂模型，也可以实现低预测误差。**此外，SRBench[26]提出了目标和估计方程之间的一致百分比。但是在这种情况下，1）完全不匹配的方程和 2）只差一个项的方程都同样被视为不正确。因此，在SRSD中，它被认为是一种粗分辨率的准确性评价方法，它仍然需要对现实世界的应用进行更多讨论。SR的一个关键特征是它的可解释性，一些研究[26, 49]使用预测表达的复杂性作为评价指标（越简单越好）。然而，它是基于一个很大的假设，即一个更简单的表达可能更有可能是数据中隐藏的规律（科学发现，如物理规律），但这对SRSD来说可能并不是这样。因此，目前还没有提出单一的评价指标来同时考虑到可解释性和估计表达式与真实表达式的接近程度。

为了解决这些问题，我们提出了新的SRSD数据集，引入了新的评估方法，并使用代表性的SR方法和Symbolic Transformer进行了基准实验。考虑到物理学公式的特性，我们仔细审查并设计了新数据集的注释策略。此外，鉴于公式可以表示为树状结构，我们在树状结构上引入了一个归一化的编辑距离，以对不完全匹配真实公式的预测公式进行定量评估。利用提出的SRSD数据集和评价指标，我们对一组SR基线进行了基准实验，发现在新的评价指标方面仍有很大的改进空间。

2 Related Studies

2.1 SRSD: Symbolic Regression for Scientific Discovery

Schmidt & Lipson[42]对科学发现的符号回归进行了先驱性研究，他们提出了一种数据驱动的科学发现方法。他们从标准的实验系统中收集数据，如本科物理教育中使用的数据：一个空气轨道振荡器和一个双摆。他们提出的算法从数据中检测不同类型的规律，如位置流形、能量规律、运动方程和力的总和规律。

这种数据驱动的科学发现方法已被各领域学者用至物理、应用机械学、气候学、材料学和化学等领域。这些研究在不同的领域利用了符号回归。一般的符号回归任务使用具有有限抽样领域的合成数据集作为基准，而许多SRSD研究则收集来自真实世界的数据，并讨论我们如何利用符号回归实现科学发现。

虽然SRSD任务与一般的符号回归（SR）任务有着相同的输入-输出（即输入：数据集，输出：符号表达式），但我们在本研究中把SRSD任务与一般的SR任务区分开来，即包括真实符号表达式的数据集是否以科学发现的合理现实假设创建，如真实符号表达式的含义（是否有物理含义）和输入变量的采样域。

2.2 Dataset and Evaluation

对于符号回归方法，存在几个基准数据集和经验研究。Feynman符号回归数据库[48]是最大的符号回归数据集之一，它由100个基于Feynman物理讲座的物理启发方程组成。通过从小范围的数值中随机抽样，他们为这100个方程生成了相应的表格数据集。受[14, 17, 19]的启发，Uy等人[50]提出了10个不同的实值符号回归问题（函数），并创建了相应的数据集（又称Nguyen数据集）。提出函数由1个或2个变量组成，例如，f (x) = x6 + x5 + x4 + x3 + x2 + x和f (x, y) = sin(x) + sin(y2)。他们通过随机抽取20-100个数据点来生成每个数据集。

La Cava等人[26]设计了一个名为SRBench的符号回归基准，并利用现有的符号回归数据集，如Feynman符号回归数据库[48]和ODE-Strogatz资源库[23]，进行了综合基准实验。在SRBench中，符号回归方法的评估方法是：1）基于目标值和估计值之间的平方误差的误差指标，以及2）显示与真实模型（方程）相匹配的估计符号回归模型的百分比的解率。然而，这些数据集和评估不一定是为了讨论科学发现的符号回归。在第3.1节和第4.1节，我们进一步描述了先前研究中的潜在问题。

3 Datasets

3.1 Issues in Existing Datasets

1. 没有物理意义：许多现有的符号回归数据集[14, 17, 19, 50]不一定是受物理学启发，而是随机生成的，例如，f (x) = log(x), f (x, y) = xy + sin((x - 1)(y - 1)) 。为了讨论符号回归在科学发现方面的潜力，我们需要进一步阐述数据集和评估指标，考虑我们在实践中如何利用符号回归。
2. 采样过程过于简化：虽然有些数据集是受物理学启发的，如Feynman符号回归数据库（FSRD）[48]和ODE-Strogatz资源库[23]，但它们的采样策略非常简化。具体来说，这些策略没有区分常数和变量，例如，光速被视为一个变量，并在1到5的范围内随机取样。 此外，大多数取样域与我们在现实世界中观察到的数值相差甚远，例如，表S1中的II.4.23（真空辐射率的取样范围为1到5）。当分布的采样范围很窄时，我们无法区分洛伦兹变换和伽利略变换，例如表S3中的I.15.10和I.16.6，表S5中的I.48.2，表S7中的I.15.3t、I.15.3x和I.34.14，或者黑体辐射可能被误估为斯蒂芬-波尔兹曼定律或维恩位移定律，例如表S8中的I.41.16。
3. 重复的公式：鉴于以上两个问题，现存数据库中的许多公式都是重复的。例如，如表1所示，原始费曼符号回归数据库中的F=μNn（I.12.1）和F=q2E（I.12.5）被认为是相同的，因为这两个方程都是乘法的，由两个变量组成，其采样域（表1中的分布）完全相同。例如，原始FSRD中大约25%的符号回归问题在这方面有1-5个重复的。
4. 公式不正确或不合适：Feynman符号回归数据库[48]将每个变量都视为浮点数，而它们应该是整数才有物理意义。例如，布拉格定律中的相位差数应该是整数，但采样为实数（表S1中的I.30.5）。此外，他们甚至没有对角度变量进行特殊处理（表1中的I.18.12, I.18.16和I.26.2）。在物理上，一些变量可以是负值，而原始的费曼符号回归数据库[48]只采样正值（例如表S3中的I.8.14和I.11.19）。我们也避免在方程中使用arcsin/arccos，因为在Feynman符号回归数据库[48]中使用arcsin/arccos只是为了获得角度变量，没有实验意义（表1中的I.26.2，表S1中的I.30.5，以及表S11中的B10）。原始注释中使用arcsin和arccos的方程式是I.26.2（斯内尔定律）、I.30.5（布拉格定律）和B10（相对论畸变）。这些都是描述与两个角度有关的物理现象，只用反函数来描述其中一个角度，是一种不自然的变形。此外，反函数的使用隐含地限制了角度的范围，但在实际的物理现象中却没有这种限制。

3.2 Proposed SRSD Datasets

我们通过提出基于FSRD[48]中使用的方程的新的SRSD数据集来解决上述现有数据集中的问题。即第3.1节总结了FSRD和我们的SRSD数据集之间的区别。我们的注释政策是精心设计的，以模拟典型的物理实验，这样SRSD数据集就可以参与研究界的科学发现的符号回归的研究。

3.2.1 Annotation policy

我们从FSRD[48]的注释中彻底修订了每个变量的采样范围。首先，我们审查了每个变量的属性，并将物理常数（如光速、引力常数）视为常数，而此类常数在原始FSRD数据集中被视为变量。接下来，定义了变量范围，以对应每个典型的物理实验，确认每个方程式的物理现象。我们还使用[36]作为参考。在具体实验难以假设的情况下，设定了可以看到相应物理现象的范围。一般来说，范围被设定为在其阶数内的对数尺度上取样为$10^2$，以便随着阶数的变化，取大和小的数值变化。诸如角度这样的变量，对于其线性分布的预期，被设定为均匀地取样。此外，采取特定符号的变量被设定为在该范围内取样。表1和S1-S11显示了原始FSRD和我们提出的SRSD数据集之间的详细比较。

3.2.2 Complexity-aware Dataset Categories(复杂度感知的数据集类别)

虽然提议的数据集由120个不同的问题组成，但为所有问题单独训练一个符号回归模型将需要的训练成本也不容小觑，即有120次单独的训练来评估符号回归方法。为了在评估科学发现的符号回归模型时有更大的灵活性，我们根据数据集的复杂性定义了三个群组。易、中、难三组，分别由30、40和50个不同的问题组成。

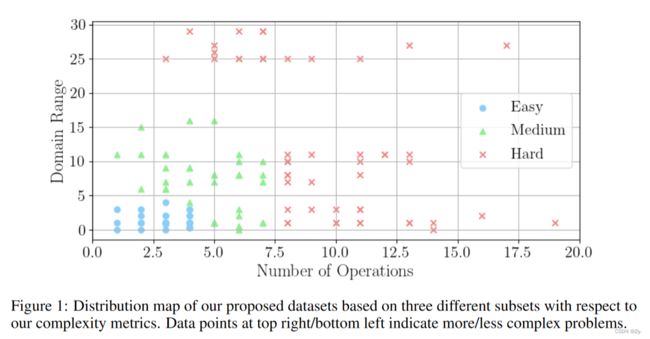
我们定义了问题的复杂性，用操作符的数量来表示真正的方程树和采样域的范围。前者衡量有多少数学运算组成了真正的方程，如加、乘、幂、幂和对数运算（见图2）。后者考虑采样分布的量级大小（表1和S1-S11中的分布栏），当从广泛的分布中采样时，会增加复杂性。

本文定义的域范围为：

其中，S表示一个给定的符号回归问题的采样域（分布）的集合。正如我们将在第5.3节中所展示的，这些群组代表了高水平的问题困难。例如，这些子集将帮助研究界在短期内对Easy集（30个问题）进行调整和/或对新方法进行理智检查，而不是使用整个数据集（120个问题）。图1显示了我们提出的数据集的三种不同的分布图。简单、中等和困难集分别由30、40和50个单独的符号回归问题组成。

4 Benchmark

除了传统的指标，我们在第4.1节中提出了一个新的指标来讨论科学发现的符号回归的性能。根据这套指标，我们设计了一个用于科学发现的符号回归评价框架。

一般来说，很难定义符号回归模型的 “准确性”，因为我们将把它的估计方程与ground-truth方程进行比较，需要标准来确定它是否 “正确”。La Cava等人[26]提出了符号解的合理定义，旨在捕捉与真实模型相差一个常数或标量的符号回归模型。他们还使用了R2得分（公式2），并将模型满足R2>τ的符号回归问题的百分比定义为准确性，其中τ是一个阈值，例如，[26]中τ=0.999。

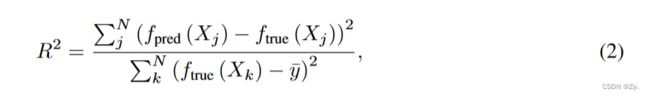
其中N表示测试样本的数量（即测试数据集中的行数）$\hat{y}$是ftrue产生的目标输出的平均值。 $f_{pred}$和$f_{true}$分别是训练好的SR模型和真实模型。然而，这两个指标仍然是二元的（正确与否），或者需要一个阈值，并不能解释估计的方程在结构上与真实方程的接近程度。虽然符号回归的一个关键特征是它的可解释性，但是没有一个评价指标可以同时考虑到可解释性和估计表达式与真实表达式的接近程度

为了提供更多的灵活性，并以这种方式评估估计的方程，我们建议使用估计方程和ground-truth方程之间的编辑距离，将方程处理为树。虽然编辑距离已被用于不同的领域，如机器翻译[41]（基于文本的编辑距离），其主要用途是研究遗传编程方法的搜索过程[5, 35, 37]。与之前的工作不同，我们提出使用基于树的编辑距离作为SRSD的解决方案质量的新指标。

对于一对两棵树，编辑距离计算出用一连串的操作符将一棵树转化为另一棵树的最小成本，每一个操作要么是1）插入，2）删除，3）重命名一个节点。在这项研究中，一个节点可以是一个数学操作（如加法，exp为符号），一个变量符号，或一个常数符号。关于该算法的细节，我们请读者参考[61]。

如图2所示，我们通过以下方式对方程进行预处理：1）将常数值（如π和普朗克常数）代入表达式；2）将所得表达式转换为方程树，表示用简化符号对方程进行前序遍历。值得注意的是，在生成方程树之前，我们通过sympy，一个用于符号数学的Python库将方程简化并转换为浮点近似值。它可以帮助我们持续地将一个给定的方程映射到唯一的方程树上，并计算真实方程树和估计方程树之间的编辑距离，因为我们的评估兴趣在于估计方程的简化表达，而不是SR模型如何产生方程。例如，“x + x + x”、"4 ∗ x - x "和 "x + 2 ∗ x "将被sympy简化为 "3 ∗ x "并被认为是相同的。

对于编辑距离，我们使用Zhang & Shasha[61]提出的方法。考虑到编辑距离值的范围取决于方程的复杂性，我们将0到1的距离归一化为

$f_{pred}$和$f_{true}$分别为估计和真实的方程树。d(fpred, ftrue)是fpred和ftrue之间的编辑距离。|ftrue|表示组成方程ftrue的树节点的数量。我们注意到，这个指标是为了捕捉估计方程和真实方程之间的相似性，因此系数值本身（如图2中C1的值）应该不重要。

4.2 Evaluation Framework

对于真实的数据集（假设是观察到的数据集），只有表格式的数据可以用于训练和验证。(在实践中，测试数据集不包括真实方程。)为了基准的目的，除了测试表格数据外，真实方程也作为测试数据提供。对于每个问题，我们使用验证表格数据集，并从F中选择最佳训练的SR模型$f_{pred}^{\ast }$，F是一个用给定方法，即公式（4），训练的模型集。

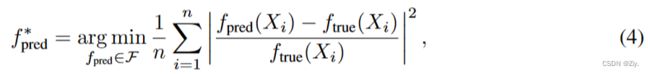
请注意，虽然我们在第4.1节中提出了估计方程树和真实方程树之间的归一化编辑距离，但这种真实方程在实践中不会出现，特别是在使用符号回归方法进行科学发现时。出于这个原因，我们使用预测值与验证表数据集之间的几何距离来选择通过超参数调整得到的最佳模型。使用每个方法的最佳模型，我们计算归一化的编辑距离来评估该方法。

5 Experiments

5.1 Baseline Methods

对于基线，我们使用SRBench[26]中最好的五种符号回归方法。具体来说，我们选择gplearn[22]、AFP[43]、AFP-FE[42]、AI Feynman[49]和DSR[40]，参考他们研究中FSRD数据集的解决率排名。我们注意到La Cava等人[26]也对黑箱问题的符号回归方法进行了基准测试，这些问题的真实符号表达式是未知的，其他符号回归方法如Operon[21]、SBP-GP[53]、FEAT[24]、EPLEX[25]和GP-GOMEA[54]在R2驱动的准确性方面超过了我们从他们的研究中选择的五个基线方法。然而，我们发现解决率与编辑距离更为一致，因此我们选择了SRBench[26]中针对FSRD数据集的经验显示的解决率方面最好的五种符号回归方法。除了现有的五种符号回归基线外，我们还引入了Symbolic Transformer，这是一个基于Transformer[52]的新基线模型。

1. gplearn[22]：一种基于遗传编程的符号回归方法，以Python包gplearn的形式发布。
2. AFP[43]：Age-fitness pareto optimization（–拟合帕累托优化）
3. AFP-FE[42]。带有拟合估计的AFP优化。
4. AI Feynman [49]：一种产生符号回归的迭代方法，以寻求将数据拟合到帕累托最优的公式。
5. DSR：基于强化学习的深度符号回归
6. Symbolic Transformer（ST）：我们基于转化器的符号回归基线。

关于基线模型的细节，我们请读者参考相应的论文[22, 40, 42, 43, 49]。我们在C节提供了Symbolic Transformer的细节，包括我们的预训练策略。虽然Symbolic Transformer本身是一个新模型，但我们注意到这项工作的主要贡献在于科学发现的数据集和符号回归的基准。我们基于Transformer的基线方法只是受到了深度学习的最新进展的启发，特别是基于Transformer的高性能、现代和灵活的模型，如[8, 9, 52]。因此，新模型的设计并不一定要比现有的基于Transformer的符号回归模型[4, 51]包括当代的工作如[18]有所改进。

5.2 Runtime Constraints

第5.1节中的基线方法的实现，除了Symbolic Transformer 9，没有使用任何GPU。我们总共运行了600个高性能计算（HPC）作业，使用 "C.small "和 "C.large "计算节点，这些节点有5-20个分配的物理CPU核，30-120GB内存，以及AI Bridging Cloud Infrastructure（ABCI）10中的720GB本地存储。

1. 由于资源有限，每个HPC作业被设计为最多运行24小时，我们用一对目标表格数据集和一个符号回归方法来运行一个作业。
2. 给定一对数据集和方法，我们的每个HPC作业最多运行100个具有不同超参数值的独立训练会话。

5.3 Results

在这一节中，我们讨论了我们的基线方法的实验结果，使用本文提出的SRSD数据集。表2和表3分别显示了符号回归基线方法在R2驱动的准确性（R2>0.999）和解决率方面的表现，这两个指标都是在SRBench中使用的[26]。根据这些指标，DSR明显优于我们考虑的所有其他基线。DSR的结果也表明了我们的SRSD数据集的三个类别的难度水平，这看起来与我们的复杂性感知数据集分类（第3.2.2节）相一致。

现在我们讨论使用归一化编辑距离的结果。表4显示了基线方法在归一化编辑距离方面的结果。有趣的是，虽然Symbolic Transformer在表2中基于R2的准确度方面表现最差，但它在所有SRSD简单、中等和困难集上取得了最好的归一化编辑距离，并大大提升了DSR。这一趋势也意味着，基于R2的准确度并不总是表明SR模型能够产生一个结构上接近真实方程的方程的程度。我们还证实，每组SRSD数据集的难度都反映在表2-4的整体趋势上。

6 Limitations

6.1 Implicit Functions

符号回归在推断隐性函数方面通常有一个限制，因为如果对变量没有限制，模型会推断出一个常规常数函数。例如，f (x, y) = 0被推断为0 = 0 ∀x, y。这个问题可以通过应用推断的函数应该至少依赖于两个变量的约束来解决，例如。推断f (x, y) = 0，∂f ∂x 6= 0，∂f ∂y 6= 0，或者将函数转换为明确的形式，例如y = g(x)。如第3.1节所述，我们将数据集中的一些函数转换为显式形式，避免了反三角函数。

6.2 Dummy Variables and Noise Injection

当把机器学习应用于现实世界的问题时，往往是这样的：1）不是所有观察到的特征（符号回归中的变量）都是解决问题所必需的，2）观察到的值包含一些噪声。虽然我们遵循[26]，并在E节中展示了我们的SRSD数据集的实验结果，有噪声注入的目标变量，但这些方面在本研究中没有彻底讨论，这样的讨论可以是建立在这项工作上的另一篇论文，并进一步参与科学发现的符号回归的研究。

7 Conclusion

在这项工作中，我们指出了科学发现的符号回归（SRSD）现有数据集和基准的问题。为了解决这些问题，我们提出：1）120个新的SRSD数据集，基于FSRD[48]中的一组物理公式；2）一个新的SRSD评价指标，讨论真实和估计的符号表达式（方程）之间的结构相似性。我们注意到，本研究认为，归一化编辑距离这个指标不是为了取代现有的SR指标，而是为了纳入这些指标（例如表2和表4）。除了上述主要贡献，我们提出了一个基于Transformer的符号回归基线，命名为Symbolic Transformer，该基线在拟议的SRSD数据集上取得了最佳的归一化编辑距离。为了鼓励对SRSD的研究，我们公布了我们的数据集1、2、3和代码库4，采用MIT许可证。

A Our SRSD Datasets: Additional Information

数据集详细信息说明，Git里面也有

B Hyperparameters for Five Existing SR Baselines

表S12显示了现有五个符号回归基线的超参数空间。gplearn[22]12、AFP[43]和AFP-FE[42]13的超参数是由Optuna[2]优化的，这是一个超参数优化框架

C Symbolic Transformer

C.1 Architecture Design

Symbolic Transformer是一个编码器-解码器网络，用于预测与输入表格数据点相对应的二进制方程树。编码器输入方程中的采样表格数据，并输出variable-wise的特征。将这些特征作为解码器的输入，并以自回归的方式输出token的前序序列，以建立一个二进制方程树。

首先，我们描述了一个输入表格数据并输出variable-wise特征的编码器。这里的表格数据具有以下特性。

• 每一行是一个从预期方程中取样的数据点
• 每一列对应于方程的输入变量（x1, x2, - - ）或方程的输出（y）。

对于这样的数据，希望输入的表格数据和输出方程之间的关系具有以下特性。

• 每一行的不变性；由于每个采样点之间的顺序没有意义，无论行如何重新排列，输出方程都不会改变。
• 每一列和变量的排列相等性；当输入表格数据的列被重新排列时，预计输出方程中的变量顺序将与输入列相对应而改变。(例如，假设公式y = x1 - x2，如果输入表格数据的x1列和x2列互换，预期输出为y = x2 - x1。)

为了解决这种排列不变性和排列相等性的数据结构，可以参考处理三维点云的PointNet[6]和处理集合数据的Deep Sets[60]的思路。这些论文中提出的方法是利用共享多层感知器（MLP）的逐点转换（排列相等性操作）和利用Pooling（排列不变性操作）的聚合。

当应用于表格数据时，通过结合Shared MLP和column-wise（variable-wise）pooling可以得到一个样本的point-wise特征。同样，通过结合Shared MLP和row-wise（样本point-wise）Pooling，可以得到一个variable-wise特征。在这两种操作中，通过聚合一次，然后将特征与每个单元的特征结合起来（这种想法被用于PointNet[6]中的语义分割网络），可以预见，聚合方向的整个信息将传播到每个单元。我们把这种操作称为特征拼接(feature splatting.)。请注意，它是一个排列不变性的操作。

拟议的网络结构如图S1所示。拟议的编码器由两个编码块组成，每个编码块包括：1.) 共享MLP，2.)行级（样本点级）池化，3.)行级特征拼接，4.)共享MLP，5.)列级（变量级）池化，和6.)列级特征拼接。encoder是permutation-equivalent，每个单元的信息都会传播到行轴和列轴上。最后，row-wise（样本point-wise）池化可以得到variable-wise特征。

Decoder是一个Transformer的Decoder[52]，它将一个variable-wise特征和tokens一个的前序序列（将方程表达为二进制方程树）作为输入，并输出下一个token。下一个token是通过在从输入token得到的variable-wise特征上使用多头注意力机制来估计的。在训练过程中，我们使用教师强迫法（teacher forcing method，[58]），将ground truth前序序列中的前（j-1）个token送入解码器，用于预测第（j）个token，并使用计划采样策略（scheduled sampling strategy）计算交叉熵损失[28]。在推理过程中，解码器使用先前预测的tokens序列作为输入tokens来自动预测下一个token，如图S2所示。从产生的前序序列中，生成二进制方程树作为Symbolic Transformer的输出。

对于每个训练batch，我们也会mask下一个token的候选者，因为Symbolic Transformer会从训练批的形状中知道目标方程中潜在的最大变量数。假设一个训练batch由形状为（1,000,3）的表格数据组成，Decoder不应该预测三个或更多的unique变量token作为预排序的一部分。

值得注意的是，在预测前序序列的下一个token时，我们利用二元方程树的特性进行有效推理。由于我们预测前序序列以建立二元方程树，当从所产生的序列表达式中建立的二元方程树的所有子节点都是常数或变量符号的token时，我们可以终止下一个token的inference，即二元方程树是完整的，不能再扩展，因此我们可以终止推理而不预测""，此为标准seq2seq任务中使用的序列结束标记。