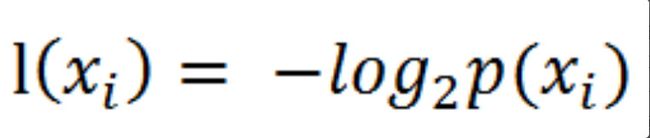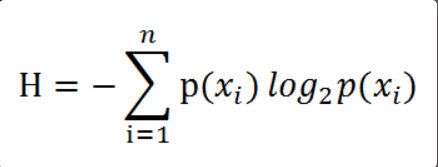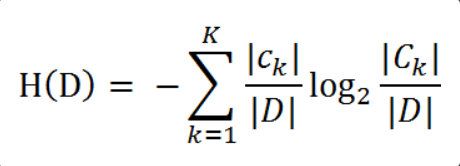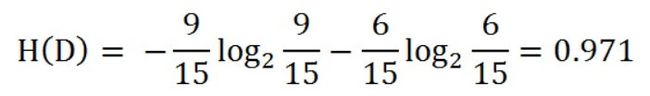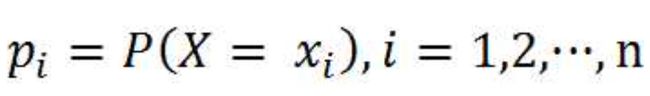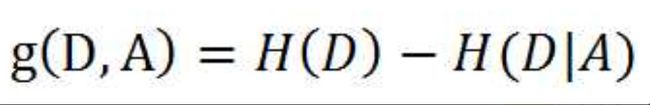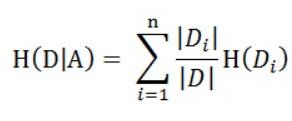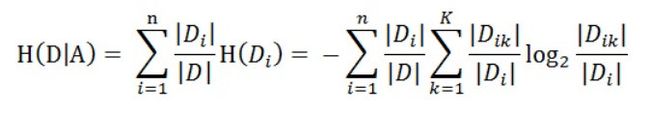机器学习系列文章-决策树

决策树

由于我们是使用sklearn对决策树代码进行实现，所以并不是很关心其原理部分。但我仍需要对其进行一定的了解。通过查询资料，去学习了下决策树的原理，这里对其原理进行简要介绍。

注：这里决策树的原理是通过这个网站来学习的，这里只做记录。

机器学习实战教程（二）：决策树基础篇之让我们从相亲说起 (cuijiahua.com)

决策树原理

决策树是一种基本的分类与回归方法。决策树可以这样理解为：由决策树的根结点到叶结点的每一条路径构建一条规则，路径上内部结点的特征对应着规则的条件，而叶结点的类对应规则的结论。

分类决策树

分类决策树模型是一种描述对实例进行分类的树形结构。

决策树构成

决策树由结点和有向边组成。

结点类型

有两种类型内部结点和叶结点

内部结点

表示一个特征或者属性

叶结点

表示一个类

构造决策树

一般可以分为特征选择、决策树生成、决策树修剪

特征选择

特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。通常特征选择的标准是信息增益或信息增益比。

信息增益

信息增益是在划分数据集后信息发生的变化。那么如何计算信息增益？

信息增益的计算，需要引入熵这个名词，全称为香农熵，是集合信息的度量方式。数学上的解释是：信息的期望值。在信息论和概率统计中，熵是表示随机变量不确定性的度量。

香农熵

在计算事物的信息期望值之前，我们需要先计算事物的类别信息。设p(xi)是选择该分类的概率，可以通过这个公式，计算得到所有类别的信息。

为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值（数学期望）。公式是

其中n是分类的数目，熵越大，随机变量的不确定性就越大。当熵中的概率由数据估计(最大似然估计)得到时，所对应的熵被称为经验熵。这个概率事可以通过数据数出来的。我们假设训练数据集为D，则训练数据集D的经验熵为H(D)，|D|表示样本容量，即样本个数。假设分为K个类Ck=1,2,3,…K,|Ck|为属于类Ck的样本个数，因此经验熵就可以写作：

根据此公式，我们可以计算出经验熵。经验熵可以用来分析样本数据中的数据，从而进行分类。

比如：假设有15个样本数据的数据集。9个数据属于类别A，6个数据属于类别B，通过上面的公式我们可以对该数据集进行经验熵的计算。

对上面计算公式的解释：K=2、ck的值在类别A时等于9，在类别B时等于6、D是样本个数15、Ck的值在属于类别A时是类别A的样本个数9，在属于类别B时是类别B的样本个数6。

构建代码

具体的代码编写计算经验熵（香农熵）的过程可以看上面的博客，讲的很好，或者参考《统计学习方法》这本书在github上的实现代码。

条件熵

上面我们详细解释了香农熵，但是还有个定义是条件熵。条件熵是什么？条件熵一般用H(Y|X)来表示，表示在已知随机变量X的条件下，随机变量Y的不确定性。也叫做随机变量X给定的条件下随机变量Y的条件熵。定义为X给定条件下Y的条件概率分布的熵对X的数据期望

其中

同理，当条件熵中的概率由**数据估计（极大似然估计）**得到时，所对应的熵就被叫做条件经验熵。

讲了这么多条件熵、条件经验熵能用来干什么？

可以用来计算信息增益。信息增益是相对于特征而言的，信息增益越大，特征对分类结果的影响就越大，用来分类效果就会越好。

信息增益计算

特征A对训练集D的信息增益g(D,A)，可以定义为，集合D的经验熵H(D)与特征A给定条件下的条件经验熵H(D|A)之差。即

一般地，熵H(D)与条件熵H(D|A)之差称为互信息。

比如：假设特征A有n个不同的取值{a1,a2,···,an}，我们可以根据特征A的不同取值把数据集D划分成n个子集{D1,D2，···,Dn}。其中|Di|表示Di的样本个数。

根据上面的H(Y|X)计算公式，我们可以计算H(D|A)就等于

而又根据上面计算H(D)的公式，我们可以计算H(Di)的值，为

其中Dik表示Di中属于Ck的样本集合，即Dik = Di ∩ Ck，|Dik|表示样本个数。

因此我们就可以计算出来这个特征A对于数据集D的条件经验熵为

得到条件经验熵，根据上面的公式我们就可以计算其信息增益值为

构建代码

具体的代码，依然可以看上面的博客。讲的很好，或者参考《统计学习方法》这本书在github上的实现代码。这里就不写了。

根据上面的解释，我们就可以计算出对于数据集D来说的各项特征数据的信息增益值。选取其中信息增益值最大的特征来作为分类的特征。

计算了这么多，到底有什么用呢？

可以用来构造决策树。其工作原理是：当得到一份数据集时，我们可以基于其属性堆数据集进行划分，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分，第一次划分之后，数据集被向下传到树的分支的下一个结点，在这个结点我们可以再次进行数据划分，通过递归的原则对数据集进行处理，即可构建决策树。

构建决策树的算法有很多。比如C4.5、ID3和CART。

决策树生成算法递归地产生决策树，直到不能继续下去未为止。这样生成的决策树对训练数据的分类会很好，但是对于未知数据的分类就会出现过拟合。过拟合的原因是在学习时过多地考虑如何提高训练数据的正确分类，而使得构建的决策树过于复杂，这时候就需要进行决策树剪枝。

构造决策树-ID3算法

这里采用的算法是ID3算法进行实现的。这个算法的核心是在决策树各个结点上对应信息增益准则选择特征，递归地构建决策树。跟我们上面所描述的很契合。ID3相当于用极大似然法进行概率模型的选择。

具体构建方法

从根节点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为其结点的特征，由该特征的不同取值建立子节点。再对子节点递归地调用以上方法，构建决策树，直到所有特征地信息增益均很小或者没有特征可以选择为止。最后得到一颗决策树。

构建代码

代码部分还是去参考这个博客或者《统计学习方法》这本书在github上的实现代码。

在递归构建决策树时，递归有两个终止条件：第一个停止条件是所有的类标签完全相同，则直接返回该类标签；第二个停止条件是使用完了所有特征，仍然不能将数据划分仅包含唯一类别的分组，即决策树构建失败，特征不够用。此时说明数据纬度不够，由于第二个停止条件无法简单地返回唯一的类标签，这里挑选出现数量最多的类别作为返回值。

决策树做预测

流程

收集数据→准备数据→分析数据→训练算法→测试算法→使用算法

使用算法进行分类

依靠训练数据构造了决策树之后，我们可以将它用于实际数据的分类。在执行数据分类时，需要决策树以及用于构造树的标签向量。然后，程序比较测试数据与决策树上的数值，递归执行该过程直到进入叶子结点；最后将测试数据定义为叶子结点所属的类型。在用决策树做预测的时候，我们按顺序输入需要的分类结点的属性值即可。

决策树的存储

我们可以通过使用Python模块pickle序列化对象的方式，把训练的模型进行存储。使用pickle.dump存储决策树。在使用时使用pickle.load进行载入即可。

以上，便是决策树的原理，包括了其数学介绍和代码构建思路。当然，决策树可做的不仅仅只有这么多。这里只是对其的简要介绍。也没有添加代码这样。大家凑合看吧。