神经网络拟合二元函数曲面实践
简介
Andrew Ng 深度学习课程的第一周第三次作业是实现一个浅层神经网络,课程方给的框架很有意思,但该作业的输出是类别,我想实践一下该网络能否改造用来解决回归问题,具体而言是拟合一个函数z = x2+y2 ,尝试之后发现效果不是很稳定,容易收敛到局部极小值,但拟合效果大体上还能接受,简要分享,后续准备改用随机梯度下降方法来跳出局部极小值。
神经网络结构
因为是二元函数,所以输入层维度固定为2,输出层维度为1,输出层未采用激活函数,隐藏层只用了一层,设置了20个神经元,激活函数为tanh。误差函数使用均方误差函数,学习率设置为0.2。
拟合效果
绿色点是原始曲面,红色点是拟合曲面。
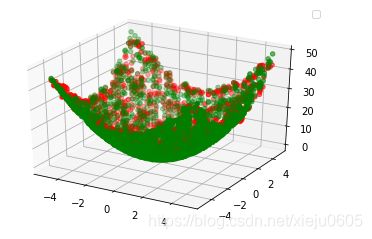
这样看可能看不出拟合的效果,放一张单独只有拟合曲面的图。
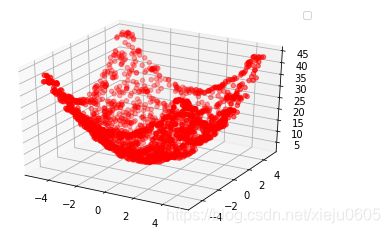
大体上还是拟合出来了,放上误差曲线。每1000次迭代取一次误差,不是很光滑,但能说明问题。
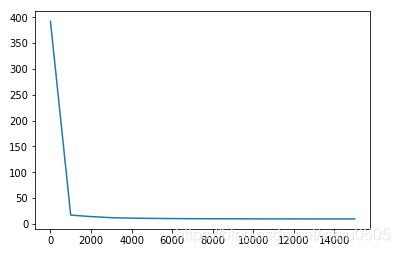
代码
下面是基本代码,框架用的是作业中提供的框架,针对连续数值的输出,我对网络结构和前向传播、后向传播做了适当修改。
# Package imports
import numpy as np
import matplotlib.pyplot as plt
import random
from matplotlib import cm
import mpl_toolkits.mplot3d
np.random.seed(2)
def layer_sizes(X, Y):
"""
Arguments:
X -- input dataset of shape (input size, number of examples)
Y -- labels of shape (output size, number of examples)
Returns:
n_x -- the size of the input layer
n_h -- the size of the hidden layer
n_y -- the size of the output layer
"""
### START CODE HERE ### (≈ 3 lines of code)
n_x = X.shape[0] # size of input layer
n_y = Y.shape[0] # size of output layer
### END CODE HERE ###
return (n_x, n_y)
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(20)
### START CODE HERE ### (≈ 4 lines of code)
W1 = np.random.randn(n_h, n_x)* 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)* 0.01
b2 = np.zeros((n_y, 1))
### END CODE HERE ###
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def forward_propagation(X, parameters):
"""
Argument:
X -- input data of size (n_x, m)
parameters -- python dictionary containing your parameters (output of initialization function)
Returns:
A2 -- The sigmoid output of the second activation
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
"""
# Retrieve each parameter from the dictionary "parameters"
### START CODE HERE ### (≈ 4 lines of code)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
### END CODE HERE ###
# Implement Forward Propagation to calculate A2 (probabilities)
### START CODE HERE ### (≈ 4 lines of code)
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = Z2
### END CODE HERE ###
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
def compute_cost(A2, Y, parameters):
"""
Computes the cross-entropy cost given in equation (13)
Arguments:
A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
parameters -- python dictionary containing your parameters W1, b1, W2 and b2
Returns:
cost -- cross-entropy cost given equation (13)
"""
m = Y.shape[1] # number of example
cost = np.sum(np.square(A2-Y))/m
cost = np.squeeze(cost) # makes sure cost is the dimension we expect.
# E.g., turns [[17]] into 17
return cost
def backward_propagation(parameters, cache, X, Y):
"""
Implement the backward propagation using the instructions above.
Arguments:
parameters -- python dictionary containing our parameters
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
X -- input data of shape (2, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
grads -- python dictionary containing your gradients with respect to different parameters
"""
m = X.shape[1]
# First, retrieve W1 and W2 from the dictionary "parameters".
### START CODE HERE ### (≈ 2 lines of code)
W1 = parameters['W1']
W2 = parameters['W2']
### END CODE HERE ###
# Retrieve also A1 and A2 from dictionary "cache".
### START CODE HERE ### (≈ 2 lines of code)
A1 = cache['A1']
A2 = cache['A2']
### END CODE HERE ###
# Backward propagation: calculate dW1, db1, dW2, db2.
### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
dZ2 =( A2 - Y)
dW2 = 1/m * np.dot(dZ2, A1.T)
db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = 1/m * np.dot(dZ1, X.T)
db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)
### END CODE HERE ###
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
def update_parameters(parameters, grads, learning_rate = 0.2):
"""
Updates parameters using the gradient descent update rule given above
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients
Returns:
parameters -- python dictionary containing your updated parameters
"""
# Retrieve each parameter from the dictionary "parameters"
### START CODE HERE ### (≈ 4 lines of code)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
### END CODE HERE ###
# Retrieve each gradient from the dictionary "grads"
### START CODE HERE ### (≈ 4 lines of code)
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
## END CODE HERE ###
# Update rule for each parameter
### START CODE HERE ### (≈ 4 lines of code)
W1 -= learning_rate * dW1
b1 -= learning_rate * db1
W2 -= learning_rate * dW2
b2 -= learning_rate * db2
### END CODE HERE ###
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
Arguments:
X -- dataset of shape (2, number of examples)
Y -- labels of shape (1, number of examples)
n_h -- size of the hidden layer
num_iterations -- Number of iterations in gradient descent loop
print_cost -- if True, print the cost every 1000 iterations
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[1]
# Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
### START CODE HERE ### (≈ 5 lines of code)
n_x, n_y = layer_sizes(X, Y)
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
### END CODE HERE ###
# Loop (gradient descent)
for i in range(0, num_iterations):
### START CODE HERE ### (≈ 4 lines of code)
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
A2, cache = forward_propagation(X, parameters)
# Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
cost = compute_cost(A2, Y, parameters)
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
grads = backward_propagation(parameters, cache, X, Y)
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
parameters = update_parameters(parameters, grads)
### END CODE HERE ###
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
def predict(parameters, X):
"""
Using the learned parameters, predicts a class for each example in X
Arguments:
parameters -- python dictionary containing your parameters
X -- input data of size (n_x, m)
Returns
predictions -- vector of predictions of our model (red: 0 / blue: 1)
"""
### START CODE HERE ### (≈ 2 lines of code)
A2, cache = forward_propagation(X, parameters)
predictions = A2
### END CODE HERE ###
return predictions
#训练集和测试集生成
if __name__ == '__main__':
train_data = np.zeros((10000,3))
for i in range(10000):
train_data[i][0] = random.uniform(-5, 5)
train_data[i][1] = random.uniform(-5, 5)
train_data[i][2] = train_data[i][0]**2 + train_data[i][1]**2
X = train_data[:,0:2].T
y = train_data[:,2].reshape(10000,1).T
parameters = nn_model(X, y, n_h = 20, num_iterations = 20000, print_cost=True)
test_data = np.zeros((2000,4))
for i in range(2000):
test_data[i][0] = random.uniform(-5, 5)
test_data[i][1] = random.uniform(-5, 5)
test_data[i][2] = test_data[i][0]**2 + test_data[i][1]**2
x = test_data[:,0:2].T
predictions = predict(parameters, x)
for i in range(2000):
test_data[i][3] = predictions[0][i]
ax = plt.subplot(111, projection='3d') # 创建一个三维的绘图工程
#将数据点分成三部分画,在颜色上有区分度
ax.scatter(test_data[:,0], test_data[:,1], test_data[:,2], c='g')
ax.scatter(test_data[:,0], test_data[:,1], test_data[:,3], c='r')
plt.legend()
plt.show()