最短路总结

目录

一、最短路的分类

二、（迪杰斯特拉）Dijkstra算法

1.算法变量

2.算法思路

3.算法模板

三、堆优化Dijkstra

四、Floyd算法

---

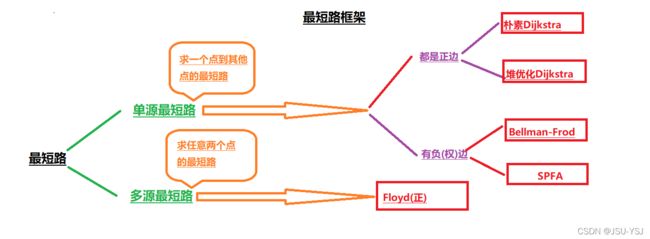
一、最短路的分类

二、（迪杰斯特拉）Dijkstra算法

1.算法变量        

• n，图的顶点数
• k，图的边数
• begin，起点下标
• end，终点下标
• map[ i ][ j ]，图的存储数组
• low[ i ]，图的最短路径状态数组
• visit[ i ]，顶点访问标记数组
• INF，不可访问标记

2.算法思路

• 初始化最短距离为直接距离，low[ i ] = map[ begin ][ i ]
• 初始化访问标记，visit数组为false
• 查找未访问的low[ i ]的最小值，记录最小下标index，并记m_len=low[ index ]，标记已访问visit[ index ] = true
• 查找未访问的low[ i ]的最小值，记录最小下标index，并记m_len=low[ index ]，标记已访问visit[ index ] = true
• 重复第3步，直到所有visit数组均为true
  low[ end ]为所求值

3.算法模板

#include 
using namespace std;
const int inf = 1e9 + 5;
const int N   = 1005;
int vis[N];
int low[N];
int Map[N][N];
int n, k;

int Dijkstra(int begin, int end) {
    // 初始化
    for (int i = 1; i <= n; i++) {
        low[i] = inf;
        vis[i] = false;
    }
    // 找到一开始的连接的边
    vis[begin] = true;
    for (int i = 1; i <= n; i++) { low[i] = Map[begin][i]; }
    for (int i = 1; i <= n; i++) {
        // 找到一个最短的，并且记录下来
        int Min = inf, idx = -1;
        for (int j = 1; j <= n; j++) {
            if (low[j] < Min) {
                Min = low[j];
                idx = j;
            }
        }
        vis[idx] = true;
        // 更新
        for (int j = 1; j <= n; j++) {
            if (low[j] > Min + Map[idx][j]) {
                low[j] = Min + Map[idx][j];
                vis[false];
            }
        }
    }
    return low[end];
}

int main(int argc, char const *argv[]) {
    cin >> n >> k;
    for (int i = 0; i < k; i++) {
        int x, y, v;
        cin >> x >> y >> v;
        Map[x][y] = v;
        Map[y][x] = v;
    }
    int begin, end;
    cin >> begin >> end;
    cout << Dijkstra(begin, end) << endl;
    return 0;
}

#include 
#define ll long long
using namespace std;
const ll inf = 2147483647;
const int N  = 1000000;

int n, m, Beg, End;
bool vis[N];
ll low[N];

// 链式前向星
struct node {
    ll to, next, v;
} edge[N];
int head[N];
int cnt = 0;

void add(int a, int b, int v) {
    cnt++;
    edge[cnt].v    = v;
    edge[cnt].to   = b;
    edge[cnt].next = head[a];
    head[a]        = cnt;
}

int Dij() {
    for (int i = 1; i <= n; i++) {
        low[i] = inf;
        vis[i] = false;
    }
    low[Beg] = 0;
    int idx  = Beg;
    while (true) {
        vis[idx] = true;
        for (int i = head[idx]; i != 0; i = edge[i].next) {
            int a = idx, b = edge[i].to, v = edge[i].v;
            if (!vis[b] && low[b] > low[a] + v) { low[b] = low[a] + v; }
        }
        ll Min = inf;
        for (int i = 1; i <= n; i++) {
            if (!vis[i] && Min > low[i]) {
                Min = low[i];
                idx = i;
            }
        }
        if (vis[idx]) break;
    }
    return low[End];
}


int main(int argc, char const *argv[]) {
    cin >> n >> m >> Beg >> End;
    for (int i = 1; i <= m; i++) {
        int a, b, v;
        cin >> a >> b >> v;
        add(a, b, v);
    }
    cout << Dij() << endl;
    return 0;
}

三、堆优化Dijkstra

这个比较简单就是引用C++ 优先队列即可，他的优化就是优化在我每次要去找最短的，如果我直接有最短的不就不需要去找了吗， 那么就是优化没有路径排序即可。

#include 
using namespace std;
const int N   = 100010;
const int inf = 0x7fffffff;
const int M   = 500010;

int n, m, s, e;
int low[N];
int vis[N];
// 链式前向星
struct edge {
    int to, v, next;
} edge[M];
int head[N];
int cnt = 0;

// 重写优先队列
struct node {
    int idx;
    int v;
    bool operator<(const node &x) const { return x.v < v; }
};
// 链式前向星
void add(int a, int b, int c) {
    cnt++;
    edge[cnt].v    = c;
    edge[cnt].to   = b;
    edge[cnt].next = head[a];
    head[a]        = cnt;
}
// 初始化
void init() {
    for (int i = 1; i <= n; i++) {
        vis[i] = 0;
        low[i] = inf;
    }
}

// Dijkstra
int Dij() {
    low[s] = 0;
    priority_queue q;
    // priority_queue q;
    q.push({s, 0});
    while (q.size()) {
        int idx = q.top().idx;
        q.pop();
        if (vis[idx]) continue;
        vis[idx] = 1;
        for (int i = head[idx]; i; i = edge[i].next) {
            int a = idx, b = edge[i].to, v = edge[i].v;
            if (low[b] > low[a] + v) {
                low[b] = low[a] + v;
                if (!vis[b]) q.push({b, low[b]});
            }
        }
    }
    return low[e];
}
int main(int argc, char const *argv[]) {
    cin >> n >> m >> s >> e;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    init();
    cout << Dij() << endl;
    return 0;
}

四、Floyd算法

复杂度最高的算法，但是是多源最短路的算法, 最简单的算法.

#include 
using namespace std;
const int N   = 105;
const int inf = 2147483647;

int n, m;
int Map[N][N];
void Folyd() {
    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= n; j ++) {
            for(int k = 1; k <= n; k ++) {
//注意一定要 i 为中间变量
                if(Map[j][k] > Map[j][i] + Map[i][k]){
                    Map[j][k] = Map[j][i] + Map[i][k];
                }
            }
        }
    }
}
int main(int argc, char const *argv[]) {
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i != j) Map[i][j] = inf;
    for(int i = 1; i <= m; i ++) {
        int a, b, c;
        cin >> a >> b >>c;
        Map[a][b] = c;
        Map[b][a] = c;
    }
    Folyd();
    for(int i = 1; i <= n; i ++) 
        for(int j = 1; j <= n; j ++) 
            cout << "从" << i << "到" << j << "最短路径:" << Map[i][j] << endl; 

        
     
    return 0;
}