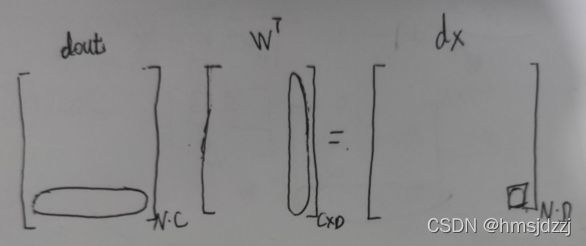CS231n 两层神经网络反向传播实现

今天写了cs231n 作业1的两层神经网络的部分，听视频和看讲义的时候觉得挺简单的没在意，后来真正写的时候发现了问题，而且也领悟到了新的东西，反向传播代码实现的奥妙之处。

同时也把之前的loss函数梯度计算给复习加深理解。

因为怕以后忘了，特来记录一下。

---

1 简单的线性的前向传播算法forward

这里比较简单，但比较烦的是x不是（N，d1,d2,d3,d4,dn）维的，需要转换乘二维的进行处理。

    x_temp = np.reshape(x, (x.shape[0], -1))

然后直接线性计算就行了，注意一下各个变量的维度

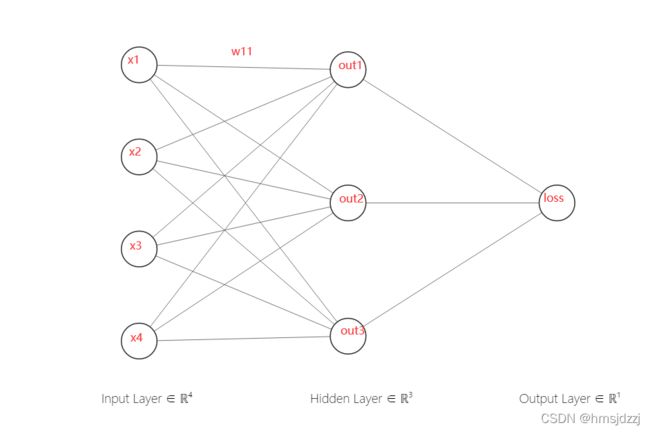
对于每个样本，有 x1*wc1+[b1,bc]=out1

    out = x_temp.dot(w)+b   #这里运用了numpy加法的特殊处理 不等于矩阵加法

---

2 反向求导 backward   ------这里是重点

最开始我以为这里是矩阵的求导，然后把矩阵拆开算了一下，发现与神经网络传播梯度是不一样的含义。因为矩阵求导中，比如AX+B=Y，DY/DX=A的含义其实是y中的元素对x中的元素分别求偏导的结果，比如x，y是2*1的向量，求导结果A则是全部的偏导结果2*2=4.

2.1 求dx

而神经网络中并不是这么一个含义，而且直接用N个样本的X矩阵可能比较难理解，我们先对X[N,D]进行一个样本一个样本的计算。X[1,D]*W+b = out[1,C]

---这里[a，b] 指矩阵规模不是索引。

 求dx，dw，db，最开始刚看这个误解了dx的意思，以为是求矩阵导数那样求out对x的偏导，后来发现维数根本就对不上，联想到这个反向传播梯度的思想，很快明白了，dx的意思是,然后就很快明白这个dout的含义了。我们要 求出全部的dx，对给个dx的求法如下：

这不就是向量【dout1，dout2，dout3】与W矩阵中一列向量，两个向量的点积么，再扩展到x2，x3，x4，再再扩展到全部的N个样本，其实就是矩阵乘法。

这样就轻松的得到了全部的dx 

2.2 求dw

因为w不是节点，是线，用刚才的网络图不好看出来，但可以通过每个矩阵的维度猜到最终答案，毕竟X和W是相乘的关系，dw【D，C】=X.T【D，N】* dout【N，C】

2.3 求db

db与上面两个有些不用，但也不叫简单，（我开始甚至以为简单到直接得1就行）。

首先我们还是看每一个样本，通过XW想乘之后，得到3个节点，b1就对应out1，b2就对应out2，b3就对应out3，所以这里就是一元的链式法则就行，db[i]=dout[i,:]。最后因为有n个样本，累加起来就可以。注意dout[i,:] 每一行是不同的，不是乘个N倍就行。

2.4 最后

感觉我一会矩阵，一会向量的， 下标啥的说的有点乱，大家尽量领会。。。。。

---

3 激活函数 relu_forward & backward

这里比较简单，但你总不能每个元素遍历去跑吧，有点小技巧，放个链接

numpy矩阵中令小于0的元素改为0_pythonplusvabel的博客-CSDN博客_numpy 将大于某个值设置为0

forward ： out = (x+abs(x) )/2

backward：     dx = dout*(x>0)

---

4 损失函数 svm & softmax  || forward & backward

之前的作业，直接放代码吧，重要点在于要用矩阵的形式解决，不然运行太慢了

1 SVM

SVM    
    num_train = x.shape[0]
    scores = x
    # 1 forward----------------------------------------------------------
    margin = np.maximum(0, scores.T - scores[range(num_train), y] + 1).T
    margin[range(num_train), y] = 0
    data_loss = np.sum(margin) * 1.0 / num_train
    reg_loss = 0
    
    loss = data_loss + reg_loss
    
    # 2 backward--------------------------------------------------------
    
    X_effect = (margin > 0).astype('float')                       # 每个样本i在非y[i]的类上产生X[i]的梯度 ,si的梯度为1
    X_effect[range(num_train), y] -= np.sum(X_effect, axis=1)   # 每个样本i在y[i]的类上产生sigma(margin gt 0)*X[i]（除y[i]的margin）的梯度
    
    dx = X_effect/num_train

2 softmax

softmax
    num_train = x.shape[0]
    # 1 forward--------------------------------------------------------------
    scores = x
    right_score = scores[range(num_train),y]
    p = np.exp(right_score) / np.sum( np.exp(scores),axis=1  )
    loss = np.sum( -np.log(p) )
    loss /= num_train
    
    # 2 backword-------------------------------------------------

    dx = ( np.exp(scores).T / np.sum( np.exp(scores),axis=1) ).T  #这里不转置不能减、除
    dx[range(num_train),y] -= 1
    dx /= num_train

有时间再补充具体的吧

---

就这三大块内容，线性计算、激活函数、损失函数，然后全部融合到一起就是整个神经网络啦，汇总到一个模板中调用呗。