[线性代数]相似对角形(秦静老师主讲)
本博文源于山东大学《线性代数》,学到了相似对角形这一章,其实也会发现对前面的知识需求还是蛮大的。如果没做到,看见题目就懵掉了,根本想不出考点别说相关定理了。博文包括以下八讲内容:
- 矩阵的相似
- 特征值与特征向量的求法
- 特征值与特征向量的性质
- 一般矩阵的相似对角形
- 实对称矩阵特征值与特征向量的性质
- 实对称矩阵的相似对角化
- 相似对角形小结
- 相似对角化习题课
矩阵的相似
相似对角形研究三块内容:特征值与特征向量/一般矩阵的相似对角化/实对称矩阵的相似对角化
矩阵相似定义
设A与B都是n阶矩阵,若存在一个n阶可逆阵P,使得
![]()
则称矩阵A与B相似,记作A~B。可逆阵P称为相似变换矩阵。
矩阵相似的性质
- 相似矩阵具有自反性、对称性、传递性。
- 相似==》等价 反之不对
- A~B==>r(A)=r(B)
- A~B==>|A|=|B|
- A~B => A 与B同时可逆或同时不可逆,且当可逆时
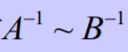
- A~B => f(A)~f(b)
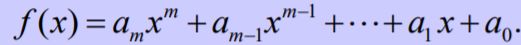
![[线性代数]相似对角形(秦静老师主讲)_第1张图片](http://img.e-com-net.com/image/info8/8d0968e4b95f4696b0857e99fa93399c.jpg)
矩阵的特征值与特征向量
设A是n阶矩阵,λ为一个数,若存在非零向量α,使Aα=λα,则称数λ为矩阵A的特征值,非零向量α为矩阵A的对应于特征值λ的特征向量。
习题
![[线性代数]相似对角形(秦静老师主讲)_第2张图片](http://img.e-com-net.com/image/info8/3847521b548246c2bd6db40fa6bc6eb5.jpg)
拿到此题,直接套用定义Aα=λα,很明显算出来,α是特征向量。判断特征值直接使用|A-λE|=0这个方法。答案都是是
特征值与特征向量的求法
数学嘛!概念先行!欲穷说理,概念先行!
Aα=λα α≠O.
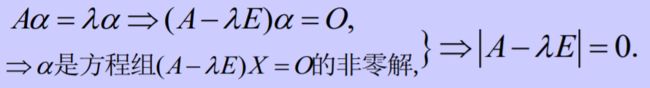
因此:满足|A-λE|=0的数λ为特征值;
方程组(A-λE)X=O的非零解为特征向量(或基础解系)
例题 求矩阵的特征值与特征向量
![[线性代数]相似对角形(秦静老师主讲)_第3张图片](http://img.e-com-net.com/image/info8/fc6750252fe14080b1778aef8b9542fd.jpg)
把A-λE摆开,然后三阶嘛,直接对角线展开,采用试根法,算出
![]()
2就是传说中的重根,把2带进去,算出特征值为2线性无关的特征向量,同理把-7带入到A-λE的式子里,
![[线性代数]相似对角形(秦静老师主讲)_第4张图片](http://img.e-com-net.com/image/info8/deb7d3006ab34e84981407844db6c30a.jpg)
求特征值与特征向量的步骤
- 解|A-λE|=0求除λ的值;即得到特征值;
- 对每一个λ,求方程组(A-λE)X=O的基础解系;即得到属于这个特征值的全部线性无关的特征向量
例题 n阶单位阵的特征值
![[线性代数]相似对角形(秦静老师主讲)_第5张图片](http://img.e-com-net.com/image/info8/7e0e2102efb740908569fca776bd4d91.jpg)
如果凶猛的话,直接用A-λE做,如果不咋地的,先做三阶找找规律,结果会发现λ等于n,或λ=0,因此n个特征值为n,0,…0(n-1个0)将0对应的特征向量,也一一算一下,会发现重根0,比较繁琐,结果特征向量是:
![[线性代数]相似对角形(秦静老师主讲)_第6张图片](http://img.e-com-net.com/image/info8/23a57b66af72446284bb95876bd873dc.jpg)
特征值与特征向量的性质
性质合集
性质1 互异特征值线性无关
性质2 相似矩阵有相同的特征值
定理合集
定理1
对任意n阶方阵A,属于不同特征值的特征向量线性无关。
特征值与特征向量的推论
例题
![[线性代数]相似对角形(秦静老师主讲)_第8张图片](http://img.e-com-net.com/image/info8/6184bee6782b4d2b8f42e21df51bfc5b.jpg)
拿到题目,证明线性无关,先把组合式写出来再说
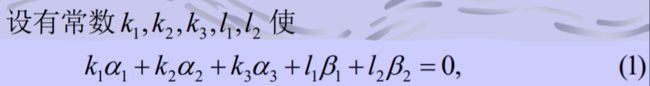
然后(1)左乘A,为什么左乘,因为Aα=λα。所以并将相关产生的等式代入
![]()
然后用λ1乘(1)式,为什么,因为这样相减可以用到互异这个概念,特别棒!
![[线性代数]相似对角形(秦静老师主讲)_第9张图片](http://img.e-com-net.com/image/info8/5720b8eccac8448398fe9a026b0e0ec0.jpg)
因为β1与β2线性无关,所以两个组合系数=0,还有就是λ1≠λ2因此
![[线性代数]相似对角形(秦静老师主讲)_第10张图片](http://img.e-com-net.com/image/info8/0cb5c271e1bc4274ac3ccc999e097da7.jpg)
最后由于α1,α2,α3线性无关得k1=k2=k3=0,从而向量组组合式线性无关,也就是(1)式子线性无关
特征值的求法公式
设λ为A的特征值,则
特征值与矩阵的关系公式
例题 练习特征值的求法公式
![[线性代数]相似对角形(秦静老师主讲)_第12张图片](http://img.e-com-net.com/image/info8/253bf89831a64a5b85c95001d7e684b9.jpg)
口算啦!|A|为特征值的乘积,A的逆就是特征值的倒数,A的特征值就是|A|/λ如A的行列式为6,λ=1则其中一个特征值为6,A^2+2A+E呢?就是把A=1,-2,-3带入就行了,比如A=1,11+2*1+1=4,整体答案是这样子滴:
![[线性代数]相似对角形(秦静老师主讲)_第13张图片](http://img.e-com-net.com/image/info8/2e6f456ba80f4685aa2ff727a1ffc091.jpg)
一般矩阵的相似对角形
前面讲了矩阵的相似基本概念,还有特征值与特征向量的简单求解。下面就要开始对一般矩阵的相似对角化展开讨论
定理1:相似充要条件
n阶矩阵A与对角阵相似的充要条件为A有n个线性无关的特征向量。
推论:互异特征值
若A有n个互异的特征值,则A与对角阵相似;但反之不对。
定理2:相异特征值与重数关系
矩阵相似对角化的步骤
例题:判断矩阵是否与对角阵相似
![[线性代数]相似对角形(秦静老师主讲)_第16张图片](http://img.e-com-net.com/image/info8/8339cdf4a0ba49969dd557e9397d8626.jpg)
求出特征值,发现特征值是互异的,因此能与对角阵相似,因此求出特征向量得出p,进而对角阵就是A矩阵的特征根
![[线性代数]相似对角形(秦静老师主讲)_第17张图片](http://img.e-com-net.com/image/info8/6f586685a82147d79cf868d0781ce519.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第18张图片](http://img.e-com-net.com/image/info8/661977a094b1437e85675216f140f44f.jpg)
实对称矩阵特征值与特征向量的性质
如果有n阶矩阵A,其矩阵的元素都为实数,且矩阵A的转置等于其本身,则称矩阵A为实对称阵。
性质1 实对称矩阵的特征值
实对称矩阵的特征值都是实数。
性质2:实对称矩阵的相异特征值
实对称矩阵的相异特征值所对应的特征向量必定正交。
性质3:实对称矩阵A的k重特征值
实对称矩阵A的k重特征值所对应的线性无关的特征向量恰有k个
推论 实对称矩阵A一定与对角阵相似
实对称矩阵A一定与对角阵相似
例题 求可逆矩阵P

拿到题目的时候,先求个特征值,发现特征值为二重的,然后算出相应的特征向量,即可得出P
![[线性代数]相似对角形(秦静老师主讲)_第19张图片](http://img.e-com-net.com/image/info8/93364590b99f4092991c4928b93951d1.jpg)
实对称矩阵的相似对角化
性质1:实对称矩阵的特征值都是实数
实对称矩阵的特征值都是实数。
性质2:实对称矩阵的相异特征值
实对称矩阵的相异特征值所对应的特征向量必定正交。
性质3 实对称矩阵A的k重特征值
实对称矩阵A的k重特征值所对应的线性无关的特征向量恰有k个。
定理1 实对称矩阵A一定与对角矩阵相似
实对称矩阵A一定与对角矩阵相似
定理2 实对称矩阵A一定与对角矩阵正交相似
实对称矩阵A一定与对角矩阵正交相似
正交阵将实对称矩阵A化为对角阵的步骤:
![[线性代数]相似对角形(秦静老师主讲)_第20张图片](http://img.e-com-net.com/image/info8/d12a248562144185855b6f7ff5a83f43.jpg)
口头总结一下:先求出矩阵的特征值,如果相异特征值,别做斯密特,然后重特征值所对应的特征向量做斯密特一下,然后单位化,排成矩阵就是对角阵咯
例题 求正交阵Q
![[线性代数]相似对角形(秦静老师主讲)_第21张图片](http://img.e-com-net.com/image/info8/0cc51c674b2541088e74d39f4ef57408.jpg)
按照步骤一步步解决,题目中A是个2重特征值,因此,要做斯密特
![[线性代数]相似对角形(秦静老师主讲)_第22张图片](http://img.e-com-net.com/image/info8/c43f481150904ba5b13b9578669213e0.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第23张图片](http://img.e-com-net.com/image/info8/e7d949935e204a378c241a15533e6a2b.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第24张图片](http://img.e-com-net.com/image/info8/0c5a05b0071c48538f10a51812122fff.jpg)
相似对角形小结
本章主要讲述:
- 特征值特征向量
- 一般矩阵的相似对角形
- 实对称矩阵的相似对角形

![[线性代数]相似对角形(秦静老师主讲)_第7张图片](http://img.e-com-net.com/image/info8/3bce5e79389a4e0f8c585c2f591d37a7.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第11张图片](http://img.e-com-net.com/image/info8/1a49c04d5bdd491faac2078c5e140574.jpg)

![[线性代数]相似对角形(秦静老师主讲)_第14张图片](http://img.e-com-net.com/image/info8/28a0303e158342e8bcb6bc82d89bf42a.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第15张图片](http://img.e-com-net.com/image/info8/302144e69b874a088cd4ac816366954e.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第25张图片](http://img.e-com-net.com/image/info8/76901eae3e894ff899718151b9a79643.jpg)
![[线性代数]相似对角形(秦静老师主讲)_第26张图片](http://img.e-com-net.com/image/info8/38dbf7efa6cf4f768b430321d0e26776.jpg)