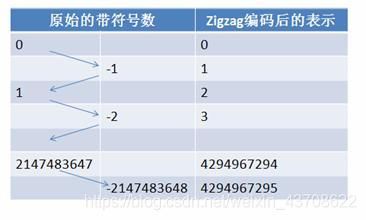
zigzag算法详解

zigzag编码的出现是为了解决varint对负数编码效率低的问题。zigzag编码的原理非常简单，就是将有符号整数映射为无符号整数。在实现上，映射通过移位即可实现，而不需要使用映射表来存储。

zigzag编码原理解析

对于正整数，可以把无意义的0去掉，只存储从1开始的"有效"数据，这样就可以压缩数据了。

例如，对于正整数1，其补码(当代计算机中实际按补码表示整数)按位展开，即为(00000000 00000000 00000000 00000001)_补，显然，我们可以只用一个字节甚至1bit来存储有效数据。

负数的补码可没有这么容易压缩。

例如，对于负数-1，(11111111 11111111 11111111 11111111)_补，全为1，并没有压缩的空间了啊！怎么办？

我们知道补码的最高位是符号位，对于负数，符号位为1，它阻碍了对于无意义0的压缩；既然有阻碍，那就得想办法解决这个阻碍；是否可以将符号位移动到补码的最后，然后数据位整体左移1位，这样就能把这个“阻碍”解决呢？

(-1)₁₀

(11111111 11111111 11111111 11111111)_补

符号位移动到最低位，数据位整体相对左移1位

(11111111 11111111 11111111 11111111)_移位

对于绝对值小的负数，冗余的前导1还是很多；似乎解决的并不彻底

把数据位按位取反，符号位保持不变

(00000000_00000000_00000000_00000001)_取反

经过移位和取反操作后，-1被“编码”成了1。如此，便能很好的压缩数据，彩！

对于非负整数，只需完成 符号位移到最低位，数据位整体左移1位

我们再来看看整数1通过同样的处理后被“编码”成什么值。

(1)₁₀

(00000000 00000000 00000000 00000001)补

(00000000 00000000 00000000 00000010)_移位

经过移位操作后，1被“编码”成了2。

似乎能得到这样的结论：

1. 对于负数，经过移位和数据位取反，也能将绝对值小的负数进行压缩；

2. 对于非负数，经过移位，也可以压缩；

那么又有一个问题来了，这两种结论怎样在代码实现层面合二为一呢？

知识点：

算术左移低位补0；算术右移，若符号位为0，高位补0；若符号位为1，高位补1；

对于n=-1(32位)，(11111111 11111111 11111111 11111111)_补

n << 1， a= (11111111 11111111 11111111 11111110)_补，数据位整体左移1位

n >> 31，b= (11111111 11111111 11111111 11111111)_补，符号位移到最低位

负数的算数右移高位补1，所以右移31位后，b为全1，这点非常重要

c=a^b， c= (00000000 00000000 0000000 00000001)_补，将-1“编码”成了1，与前面的分析一致

因为a中数据位冗余的前导1刚好与b中数据位冗余的前导1相对应，那么进行异或操作时，就能将这些冗余的前导1消除掉，数据位完成了取反动作，这样便能压缩数据了

对于n=1(32位)，(00000000 00000000 00000000 00000001)_补

n << 1， a= (00000000 00000000 00000000 00000010)_补，数据位整体左移1位

n >> 31，b= (00000000 00000000 00000000 00000000)_补，符号位移到最低位

非负数的算数右移高位补0，所以右移31位后，b全为0，这点非常重要

c=a^b，c= (00000000 00000000 00000000 00000010)_补，将1“编码”成了2，与前面的分析一致

因为0^0还是0，所以对于正整数，异或操作没有影响。

综上所述，对于32位整数，(n<<1)^(n>>31)，即能实现zigzag编码。如此精妙，彩！

搞懂了zigzag的编码原理，当然得知道怎样解码，否则就不能还原真实数值了。

zigzag解码原理解析

对于zigzag编码的值2，(00000000 00000000 00000000 00000010)_补

n >> 1， a = (00000000 00000000 00000000 00000001)_补，整体右移，还原数据位

-(n&1)，b = -(2&1)₁₀ = -(0)₁₀ = (00000000 00000000 00000000 00000000)_补，最低位按位与，取负号，还原符号位

c=a^b，c = (00000000 00000000 00000000 00000001)_补，将zigzag编码值2 解码还原成了1

对于zigzag编码的值3，(00000000 00000000 00000000 00000011)_补

n >> 1， a = (00000000 00000000 00000000 00000001)_补，整体右移，还原数据位

-(n&1)，b = -(3&1)₁₀ = -(1)₁₀ = (11111111 11111111 11111111 11111111)_补，最低位按位与，取负号，还原符号位

c=a^b，c = (11111111 11111111 11111111 11111110)_补，将zigzag编码值3 解码还原成了-2

综上所述，对于32位整数，(n>>1)^-(n&1)，即能实现zigzag解码。

c实现

// zigzag 编码
uint32_t zigzag_encode_32(int32_t val)
{
    return (uint32_t)((val<<1)^(val>>31));
}

// zigzag解码
int32_t zigzag_decode_32(uint32_t val)
{
    return (int32_t)((val>>1) ^ -(val&1));
}

运行结果

$ ./a.out -1
input num:-1
zigzag code:1,0x1
zigzag decode:-1,0xffffffffffffffff

$ ./a.out -2147483648
input num:-2147483648
zigzag code:4294967295,0xffffffff
zigzag decode:-2147483648,0xffffffff80000000

$ ./a.out 2147483647
input num:2147483647
zigzag code:4294967294,0xfffffffe
zigzag decode:2147483647,0x7fffffff

所谓数据压缩，说白了就是将不重要的数据忽略或舍弃；由于计算机中只有0和1，本质上就是将无意义的0丢弃，而起到数据压缩的目的。