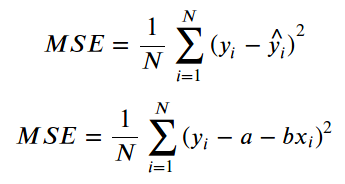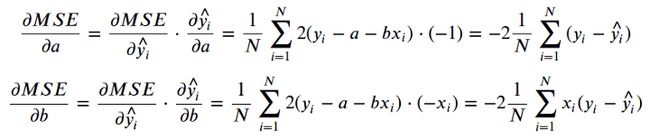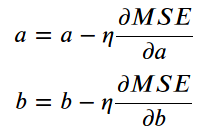案例驱动，手把手教你学PyTorch（一）

通过案例学PyTorch。

 

扫码关注《Python学研大本营》，加入读者群，分享更多精彩

介绍

PyTorch是增长最快的深度学习框架， Fast.ai在其 MOOC、Deep Learning for Coders及其库中也使用了它。

PyTorch 也非常Python 化，也就是说，如果您已经是 Python 开发人员，使用它会感觉更自然。

此外，根据Andrej Karpathy的说法，使用 PyTorch 甚至可以改善您的健康:-)

动机

周围有很多PyTorch 教程，其文档非常完整和广泛。那么，为什么要继续阅读这个分步教程呢？

好吧，尽管人们几乎可以找到PyTorch 可以做的任何事情的信息，但我错过了结构化、增量和从第一原理开始的方法。

在这篇文章中，我将引导您了解 PyTorch 使在 Python 中构建深度学习模型变得更加容易和直观的主要原因——autograd、动态计算图、模型类等等——我还将向您展示如何避免一些常见的陷阱和错误。

此外，由于这是一篇相当长的文章，我构建了一个目录以使导航更容易，如果您将其用作迷你课程并一次通过一个主题来处理内容。

目录

• 一个简单的回归问题

• 梯度下降

• Numpy中的线性回归

• PyTorch

• 自动毕业

• 动态计算图

• 优化器

• 失利

• 模型

• 数据集

• 数据加载器

• 评估

一个简单的回归问题

大多数教程都从一些漂亮的图像分类问题开始，以说明如何使用 PyTorch。它可能看起来很酷，但我相信它会分散您的主要目标：PyTorch 是如何工作的？

出于这个原因，在本教程中，我将坚持一个简单而熟悉的问题：具有单个特征x的线性回归 ！没有比这更简单的了……

简单线性回归模型

数据生成

让我们开始生成一些合成数据：我们从特征x的 100 个点的向量开始，并使用a = 1、b = 2和一些高斯噪声创建我们的标签。

接下来，让我们将合成数据拆分为训练集和验证集，打乱索引数组并使用前 80 个打乱的点进行训练。

# Data Generation
np.random.seed(42)
x = np.random.rand(100, 1)
y = 1 + 2 * x + .1 * np.random.randn(100, 1)

# Shuffles the indices
idx = np.arange(100)
np.random.shuffle(idx)

# Uses first 80 random indices for train
train_idx = idx[:80]
# Uses the remaining indices for validation
val_idx = idx[80:]

# Generates train and validation sets
x_train, y_train = x[train_idx], y[train_idx]
x_val, y_val = x[val_idx], y[val_idx]

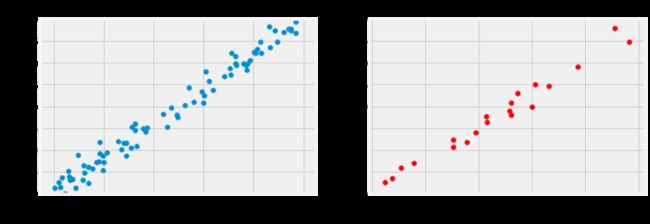
为线性回归生成合成训练和验证集

图 1：合成数据——训练和验证集

我们知道a = 1 和 b = 2，但现在让我们看看通过使用梯度下降和训练 集中的 80 个点，我们可以多接近真实值……

梯度下降

如果您对梯度下降的内部工作感到满意，请随意跳过本节。完全解释梯度下降的工作原理超出了本文的范围，但我将介绍计算梯度下降所需的四个基本步骤。

第 1 步：计算损失

对于回归问题，损失由均方误差 (MSE)给出，即标签(y) 和预测(a + bx)之间的所有平方差的平均值。

值得一提的是，如果我们使用训练集中的所有点( N ) 来计算损失，我们正在执行批量梯度下降。如果我们每次都使用一个点，那将是随机梯度下降。介于 1 和 N 之间的任何其他 (n) 都表示小批量梯度下降。

损失：均方误差 (MSE)

第 2 步：计算梯度

梯度是偏导数——为什么 是偏导数？因为人们根据（wrt）单个 参数来计算它。我们有两个参数a和b，所以我们必须计算两个偏导数。

导数告诉您当您稍微改变一些其他数量时，给定数量会发生多少 变化。在我们的例子中，当我们改变两个参数中的每一个时，我们的MSE损失会发生多大的变化？

下面等式的最右边部分是您在简单线性回归的梯度下降实现中通常看到的。在中间步骤中，我向您展示了从应用链式规则中弹出的所有元素，因此您知道最终表达式是如何形成的。

计算系数 a 和 b 的梯度

第 3 步：更新参数

在最后一步中，我们使用梯度来更新参数。由于我们试图最小化我们的损失，我们反转更新的梯度符号。

还有另一个参数需要考虑：学习率，用希腊字母eta表示（看起来像字母n），这是我们需要应用于参数更新的梯度的乘法因子。

使用计算的梯度和学习率更新系数 a 和 b 如何选择学习率？这本身就是一个主题，也超出了本文的范围。

第4步：冲洗并重复！

现在我们使用更新后的 参数返回步骤 1并重新启动该过程。

只要每个点都已经用于计算损失，一个时期就完成了。对于批量梯度下降，这是微不足道的，因为它使用所有点来计算损失——一个时期与一个更新相同。对于随机梯度下降，一个 epoch意味着N个 更新，而对于mini-batch（大小为 n），一个 epoch有N/n 个更新。

简而言之，在许多 epoch中一遍又一遍地重复这个过程，就是训练一个模型。

Numpy中的线性回归

是时候使用仅使用Numpy的梯度下降来实现我们的线性回归模型了。

等一下……我以为本教程是关于 PyTorch 的！

是的，但这样做有两个目的：首先，介绍我们的任务结构，这将基本保持不变；其次，向您展示主要的痛点，以便您充分了解 PyTorch 让您的生活更轻松:-)

为了训练模型，有两个初始化步骤：

• 参数/权重的随机初始化（我们只有两个，a和b）——第 3 行和第 4 行；

• 超参数的初始化（在我们的例子中，只有学习率和epoch 数）——第 9 行和第 11 行；

确保始终初始化随机种子，以确保结果的可重复性。像往常一样，随机种子是42，这是人们可能选择的所有随机种子中最小的随机性:-)

对于每个时期，有四个训练步骤：

• 计算模型的预测——这是前向传递——第 15 行；

• 计算损失，使用预测和标签以及手头任务的适当损失函数——第 18 和 20 行；

• 计算每个参数的梯度——第 23 和 24 行；

• 更新参数——第 27 和 28 行；

请记住，如果您不使用批量梯度下降（我们的示例使用），则必须编写一个内部循环来为每个单独的点（随机）或n个点（mini-批次）。稍后我们将看到一个小批量示例。

# Initializes parameters "a" and "b" randomly
np.random.seed(42)
a = np.random.randn(1)
b = np.random.randn(1)

print(a, b)

# Sets learning rate
lr = 1e-1
# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    # Computes our model's predicted output
    yhat = a + b * x_train
    
    # How wrong is our model? That's the error! 
    error = (y_train - yhat)
    # It is a regression, so it computes mean squared error (MSE)
    loss = (error ** 2).mean()
    
    # Computes gradients for both "a" and "b" parameters
    a_grad = -2 * error.mean()
    b_grad = -2 * (x_train * error).mean()
    
    # Updates parameters using gradients and the learning rate
    a = a - lr * a_grad
    b = b - lr * b_grad
    
print(a, b)

# Sanity Check: do we get the same results as our gradient descent?
from sklearn.linear_model import LinearRegression
linr = LinearRegression()
linr.fit(x_train, y_train)
print(linr.intercept_, linr.coef_[0])

使用 Numpy 实现线性回归的梯度下降 为了确保我们的代码没有犯任何错误，我们可以使用Scikit-Learn 的线性回归来拟合模型并比较系数。

# a and b after initialization
[0.49671415] [-0.1382643]
# a and b after our gradient descent
[1.02354094] [1.96896411]
# intercept and coef from Scikit-Learn
[1.02354075] [1.96896447]

它们最多匹配小数点后 6 位——我们使用 Numpy完全实现了线性回归。

是时候开始PyTorch了:-)

PyTorch

首先，我们需要介绍一些基本概念，如果您在全力建模之前没有充分掌握它们，可能会使您失去平衡。

在深度学习中，我们到处都能看到张量。好吧，谷歌的框架被称为TensorFlow是有原因的！到底什么是张量？

张量

在Numpy中，您可能有一个具有三个维度的数组，对吗？也就是说，从技术上讲，一个张量。

标量（单个数字）具有零维，向量 具有 一维，矩阵具有二维，张量具有三个或更多维。而已！

但是，为了简单起见，将向量和矩阵也称为张量是司空见惯的——因此，从现在开始，一切都是标量或张量。

图 2：张量只是高维矩阵

加载数据、设备和 CUDA

“我们如何从 Numpy 的数组到 PyTorch 的张量”，你问？这from_numpy就是好的。但是，它返回一个CPU 张量。

“但我想使用我喜欢的 GPU…… ”，你说。不用担心，这to()是有好处的。它将您的张量发送到您指定的任何设备，包括您的GPU（称为cuda或cuda:0）。

“如果没有可用的 GPU，我希望我的代码回退到 CPU 怎么办？”，您可能想知道…… PyTorch 再次支持您——您可以使用cuda.is_available()它来确定您是否有 GPU 可供使用，并相应地设置您的设备。

您还可以使用float().

import torch
import torch.optim as optim
import torch.nn as nn
from torchviz import make_dot

device = 'cuda' if torch.cuda.is_available() else 'cpu'

# Our data was in Numpy arrays, but we need to transform them into PyTorch's Tensors
# and then we send them to the chosen device
x_train_tensor = torch.from_numpy(x_train).float().to(device)
y_train_tensor = torch.from_numpy(y_train).float().to(device)

# Here we can see the difference - notice that .type() is more useful
# since it also tells us WHERE the tensor is (device)
print(type(x_train), type(x_train_tensor), x_train_tensor.type())

加载数据：将 Numpy 数组转换为 PyTorch 张量 如果您比较这两个变量的类型，您会得到您所期望的：numpy.ndarray第一个变量和torch.Tensor第二个变量。

但是你的好张量在哪里“生活”？在您的 CPU 或 GPU 中？你不能说……但是如果你使用 PyTorch 的type()，它会显示它的位置——torch.cuda.FloatTensor在这种情况下是一个 GPU 张量。

我们也可以反过来，将张量转回 Numpy 数组，使用numpy(). 这应该很容易，x_train_tensor.numpy() 但是……

TypeError: can't convert CUDA tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.

不幸的是，Numpy无法处理 GPU 张量……您需要先使用cpu().

创建参数

用于数据的张量（例如我们刚刚创建的张量）与用作（可训练的）参数/权重的张量有什么区别？

后面的张量需要计算它的梯度，所以我们可以更新它们的值（即参数的值）。这就是requires_grad=True争论的好处。它告诉 PyTorch 我们希望它为我们计算梯度。

您可能很想为参数创建一个简单的张量，然后将其发送到您选择的设备，就像我们对数据所做的那样，对吧？没那么快……

# FIRST
# Initializes parameters "a" and "b" randomly, ALMOST as we did in Numpy
# since we want to apply gradient descent on these parameters, we need
# to set REQUIRES_GRAD = TRUE
a = torch.randn(1, requires_grad=True, dtype=torch.float)
b = torch.randn(1, requires_grad=True, dtype=torch.float)
print(a, b)

# SECOND
# But what if we want to run it on a GPU? We could just send them to device, right?
a = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
b = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
print(a, b)
# Sorry, but NO! The to(device) "shadows" the gradient...

# THIRD
# We can either create regular tensors and send them to the device (as we did with our data)
a = torch.randn(1, dtype=torch.float).to(device)
b = torch.randn(1, dtype=torch.float).to(device)
# and THEN set them as requiring gradients...
a.requires_grad_()
b.requires_grad_()
print(a, b)

试图为系数创建变量…

第一段代码为我们的参数、梯度等创建了两个很好的张量。但它们是CPU张量。

# FIRST
tensor([-0.5531], requires_grad=True)
tensor([-0.7314], requires_grad=True)

在第二段代码中，我们尝试了将它们发送到我们的GPU的简单方法。我们成功地将它们发送到另一台设备，但我们以某种方式“丢失”了渐变......

# SECOND
tensor([0.5158], device='cuda:0', grad_fn=) tensor([0.0246], device='cuda:0', grad_fn=)

在第三块中，我们首先将张量发送到设备，然后使用requires_grad_()方法将其设置requires_grad到位True。

# THIRD
tensor([-0.8915], device='cuda:0', requires_grad=True) tensor([0.3616], device='cuda:0', requires_grad=True)

在 PyTorch 中，每个方法结束带着下划线(_) 进行更改到位, 意思是, 他们会调整基础变量。

尽管最后一种方法效果很好，但最好在创建时将张量分配给设备。

# We can specify the device at the moment of creation - RECOMMENDED!
torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
print(a, b)

实际上为系数创建变量

tensor([0.6226], device='cuda:0', requires_grad=True) tensor([1.4505], device='cuda:0', requires_grad=True)

容易多了，对吧？

现在我们知道如何创建需要梯度的张量，让我们看看 PyTorch 如何处理它们。

https://towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e

推荐书单

《PyTorch深度学习简明实战 》

本书针对深度学习及开源框架——PyTorch，采用简明的语言进行知识的讲解，注重实战。全书分为4篇，共19章。深度学习基础篇（第1章~第6章）包括PyTorch简介与安装、机器学习基础与线性回归、张量与数据类型、分类问题与多层感知器、多层感知器模型与模型训练、梯度下降法、反向传播算法与内置优化器。计算机视觉篇（第7章~第14章）包括计算机视觉与卷积神经网络、卷积入门实例、图像读取与模型保存、多分类问题与卷积模型的优化、迁移学习与数据增强、经典网络模型与特征提取、图像定位基础、图像语义分割。自然语言处理和序列篇（第15章~第17章)包括文本分类与词嵌入、循环神经网络与一维卷积神经网络、序列预测实例。生成对抗网络和目标检测篇（第18章~第19章)包括生成对抗网络、目标检测。

本书适合人工智能行业的软件工程师、对人工智能感兴趣的学生学习，同时也可作为深度学习的培训教程。

作者简介：

日月光华：网易云课堂资深讲师,经验丰富的数据科学家和深度学习算法工程师。擅长使用Python编程,编写爬虫并利用Python进行数据分析和可视化。对机器学习和深度学习有深入理解,熟悉常见的深度学习框架( PyTorch、TensorFlow)和模型，有丰富的深度学习、数据分析和爬虫等开发经验，著有畅销书《Python网络爬虫实例教程(视频讲解版)》。

购买链接（新书限时5.5折）：https://item.jd.com/13528847.html

精彩回顾

《Pandas1.x实例精解》新书抢先看！

【第1篇】利用Pandas操作DataFrame的列与行

【第2篇】Pandas如何对DataFrame排序和统计

【第3篇】Pandas如何使用DataFrame方法链

【第4篇】Pandas如何比较缺失值以及转置方向？

【第5篇】DataFrame如何玩转多样性数据

【第6篇】如何进行探索性数据分析？

【第7篇】使用Pandas处理分类数据

【第8篇】使用Pandas处理连续数据

【第9篇】使用Pandas比较连续值和连续列

【第10篇】如何比较分类值以及使用Pandas分析库

扫码关注《Python学研大本营》，加入读者群，分享更多精彩