用Python实现KNN算法(从原理到代码的实现)
用Python实现KNN算法(从原理到代码的实现)
环境
1.Pycharm
2.python3.6
声明:本栏的所有文章皆为本人学习时所做笔记而整理成篇,转载需授权且需注明文章来源,禁止商业用途,仅供学习交流.(欢迎大家提供宝贵的意见,共同进步)
原文链接https://editor.csdn.net/md?not_checkout=1&articleId=110291962
一、KNN算法的原理
1.1算法介绍
KNN的全称是K Nearest Neighbors,意思是K个最近的邻居,从这个名字我们就能看出一些KNN算法的蛛丝马迹了。K个最近邻居,毫无疑问,K的取值肯定是至关重要的。那么最近的邻居又是怎么回事呢?其实啊,KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别。
听起来有点绕,还是看看图吧。
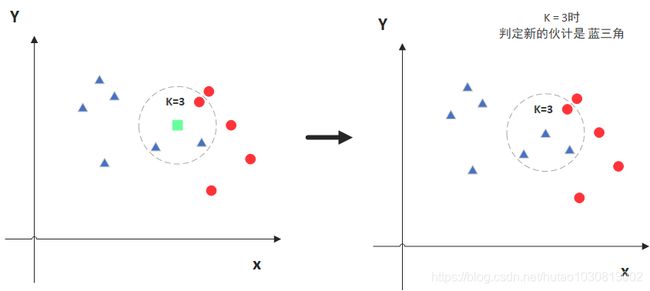
图中绿色的点就是我们要预测的那个点,假设K=3。那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。
但是,当K=5的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出K的取值是很重要的。
明白了大概原理后,我们就来说一说细节的东西吧,主要有两个,K值的选取和点距离的计算。
1.2距离d的计算和K的取值
在讲解算法实现前,我们需要回顾一点儿数学知识:两点之间的距离。
1》在二维平面内,若有两点,那么A到B的距离
D = ![]()
通过公式,我们可以从侧面看出,若D的值越小,那么A和B的距离越近,则在坐标系中A和B位置越靠近,靠的越近正是因为A和B“相似”。
通过上面那两张张图我们知道K的取值比较重要,那么该如何确定K取多少值好呢?答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
二、代码介绍
2.1数据集背景
众所周知,我们每个人的长相千差万别,但我们都有鼻子、耳朵、眼睛、脸蛋等,同时还有美丑之分,那么我们的美丑如何定义呢? 没有人敢说自己就是百分百的美女、美男,虽然如此,但我们确实又知道哪种五官令人舒服。如果说给我们每个人的长相进行分类打分的话,那我们应该依据什么来进行分类呢? 是否有具有公共特征使得被称为美女或美男的人都十分类似呢? 这是当然的,比如高鼻梁、大眼睛的人肯定比塌鼻子、小眼睛的人评分高,因此判断一个人是否到达美女、美男的要求,只需将他/她的五官与标准的精致五官进行比较便可知道,越相似说明五官越精致。那么人可以通过观察分辨,计算机如何分辨呢?
这里我们人工数据集是以鼻子、耳朵、眼睛、脸蛋这四个特征来判断人的美丑,范围从0-1,1为最高分值。
每个样本都是一个1*4的数据,这里我们一共创造了16 个样本。
对应的输出结果是五种:女神、淑女、可爱型、一般型、丑女。
2.2构造数据集和KNN模型
from numpy import * # 导入科学计算包
import operator # 导入运算符模块
import json
def createDataSet():
data = array([[1, 1, 1, 1],
[0.5, 1, 1, 1],
[0.1, 0.1, 0.1, 0.1],
[0.5, 0.5, 0.5, 0.5],
[1, 0.8, 0.3, 1],
[0.6, 0.5, 0.7, 0.5],
[1, 1, 0.9, 0.5],
[1, 0.6, 0.5, 0.8],
[0.5, 0.5, 1, 1],
[0.9, 1, 1, 1],
[0.6, 0.6, 1, 0.1],
[1, 0.8, 0.5, 0.5],
[1, 0.1, 0.1, 1],
[1, 1, 0.7, 0.3],
[0.2, 0.3, 0.4, 0.5],
[0.5, 1, 0.6, 0.6]
]);
labels = ['女神',
'淑女',
'丑女',
'一般型',
'淑女',
'一般型',
'女神',
'一般型',
'淑女',
'女神',
'丑女',
'可爱型',
'可爱型',
'淑女',
'丑女',
'可爱型'
]
return data, labels
def classify(inX,data,labels,k):
dataSetSize = data.shape[0] # 计算共有多少条训练数据
print(dataSetSize)
print('复制输入向量 用于和样本中的每条数据进行计算 [矩阵的加减乘除]')
print(tile(inX, (dataSetSize, 1)))
print(dataSetSize)
print('复制输入向量 用于和样本中的每条数据进行计算 [矩阵的加减乘除]')
print(tile(inX, (dataSetSize, 1)))
# 矩阵的减法 结果:每一项为输入向量和各个样本对应特征点的差值构成的新矩阵
diffmat = tile(inX, (dataSetSize, 1)) - data
print('\n相减后:')
print(diffmat)
sqDiffMat = diffmat ** 2 # 平方 矩阵中每一项都平方
print('\n平方后:')
print(sqDiffMat)
sqDistances = sqDiffMat.sum(axis=1) # axis=1 行向量相加 / axis=0 列向量相加
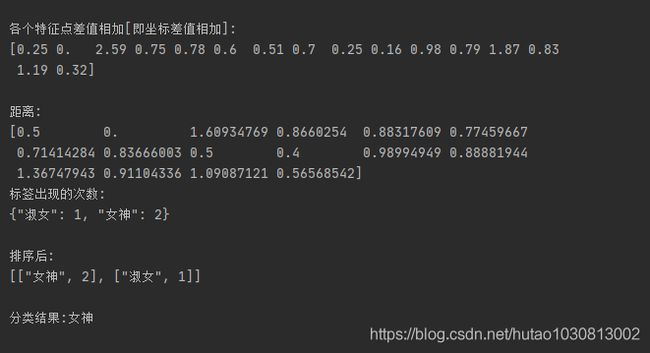
print('\n各个特征点差值相加[即坐标差值相加]:')
print(sqDistances)
distances = sqDistances ** 0.5 # 开方
print('\n距离:')
print(distances)
sortedDistIndexes = distances.argsort() # 从小到大将距离向量排序并返回其索引值
classCount = {} # dict 保存对应标签出现的次数
for i in range(k):
voteLabel = labels[sortedDistIndexes[i]] #获得类别标签
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
print('标签出现的次数:')
print(json.dumps(classCount, ensure_ascii=False))
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
print('\n排序后:')
print(json.dumps(sortedClassCount, ensure_ascii=False))
# 如: print sortedClassCount ———— [('A', 2), ('B', 1)]
return sortedClassCount[0][0] # 返回次数出现次数最多的标签2.3测试
import KNN
from numpy import*
data, labels = KNN.createDataSet()
print('测试模型分类样本数据,结果是否和样本中的分类一致')
input = [0.5, 1, 1, 1]
print('\n分类结果:'+KNN.classify(input, data, labels, 3))2.4输出结果
当K取3时,
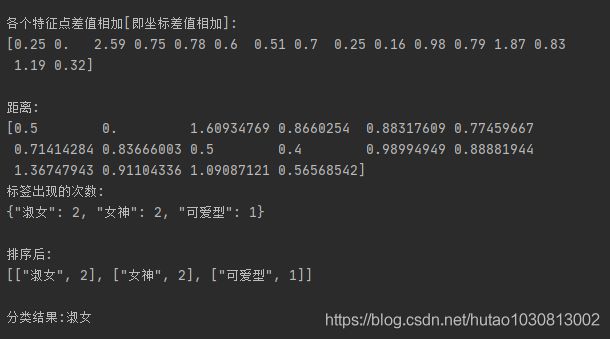
可以看出当K取不同值时,结果不同。
三、代码中一下函数用法总结
3.1tile()函数
tile()函数将变量内容复制成输入矩阵同样大小的矩阵
实例:
>>>from numpy import *
>>>minVals = array([1,1],[2,2])
>>>minVals
array([[1, 1],
[2, 2]])
>>> tile(minVals,4)
array([[1, 1, 1, 1, 1, 1, 1, 1],
[2, 2, 2, 2, 2, 2, 2, 2]])
>>> tile(minVals,(2,3))
array([[1, 1, 1, 1, 1, 1],
[2, 2, 2, 2, 2, 2],
[1, 1, 1, 1, 1, 1],
[2, 2, 2, 2, 2, 2]]
在本文中就是把输入矩阵复制成(16,1)维
3.2argsort()
numpy.argsort(a, axis=-1, kind=’quicksort’, order=None)
返回的是数组值从小到大的索引值
参数:
a为要排序的数组
axis:按哪一维进行排序
3.3classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
以文中代码为例:
classCount[voteIlabel] = classCount.get(voteLabel,0) + 1;
初始化classCount = {}时,此时输入classCount,输出为:
classCount = {}
当第一次遇到新的label时,将新的label添加到字典classCount,并初始化其对应数值为0
然后+1,即该label已经出现过一次,此时输入classCount,输出为:
classCount = {voteLabel:1}
当第二次遇到同一个label时,classCount.get(voteLabel,0)返回对应的数值(此时括号内的0不起作用,因为已经初始化过了),然后+1,此时输入classCount,输出为:
classCount = {voteLabel:2}