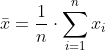Python_YBYB

PCA降维的来龙去脉及Python实现

1 PCA降维

2 在讲PCA降维的原理前需要知道的一些东西

2.1 方差

2.2 协方差及协方差矩阵

2.3 向量在不同基下的坐标

2.4 矩阵乘法

2.5 矩阵的特征值和特征向量

2.6 实对称矩阵正交相似于对角矩阵

3 PCA降维的核心思想

4 PCA降维的原理

4.1 PCA降维具体例子示范

4.2 PCA降维原理分析

5 Python实现PCA降维

1 PCA降维

随着社会的飞速发展，我们已经在分析问题或者解决问题时，经常会遇到大数据集。高维度的大数据集处理起来并非易事，不但会占用大量的资源，而且也会导致计算机运行缓慢。

一个自然的想法是，能不能删除了某一部分数据，而留下剩下的数据？这样会使得数据的复杂度降低，从而节省时间和资源，答案是肯定的。但是又会有新的一个问题出现，这样的删除是不是随意的呢？

当然不是，我们在删除的时候应该要尽可能地保留原始数据的信息，即减少因部分特征删除而导致的信息损失。考虑到大数据集的各个特征维度之间有些并不是相互独立的，有些特征具有一定的相关性。我们相信，删除与所保留特征相关性较高的数据特征，并不会造成原始数据信息的大量丢失。

例如，某电商平台的店铺数据有“浏览量”、“访问量”、“下单量”、“成交量”。“浏览量”与“访问量”并不是独立的，“浏览量”大时，我们相信“访问量”也大，“下单量”大时，“成交量”也大。当我们删除“访问量”和“成交量”这两个特征数据时，我们坚信，这样原始数据信息的损失是很小的。

因此，PCA要做的事儿就是要在以下两个方面之间做一个平衡：a.降低原始大数据集的维度（复杂度降低了）；b.使得降维后的数据集，在原来大数据集的基础上损失的信息尽可能的小。

PCA降维的应用非常广泛，它结合判别分析、聚类和回归分析等等可以解决许多实际问题。在机器学习和数据挖掘的实践中应用主要体现在以下几个方面：

（1）实现数据可视化。我们生存的物理空间是三维空间，任何三维以上的数据我们靠视觉是无法感知的。将高维数据降到低维，使得数据可视化，方便我们洞察数据背后所蕴藏的规律。

（2）缓解过拟合。特征维度越大，以为这特征越多，模型就越复杂，越容易过拟合。通过降低维度，缓解过拟合。

（3）提高计算性能。高维数据不仅占用过多的储资源，而且由于维度较高导致计算的复杂度不断上升。因此，可以通过PCA降维节约储存资源和计算资源，提高计算性能。

2 在讲PCA降维的原理前需要知道的一些东西

2.1 方差

方差和标准差是最常用来度量一组数据最常用的指标。其实，在高中的时候我们就以及熟知以下公式：

均值： $\bar{x}=\frac{1}{n}\cdot\sum_{i=1}^{n}x_{i}$

方差： $S^{2}=\frac{1}{n-1}\cdot\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$

标准差： $S=\sqrt{\frac{1}{n-1}\cdot\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}$

方差和标准差能够很好地描述一组数据的分布情况：如果一组数据越“挨的紧”或者越“拥挤”，这组数据的方差和标准差就越小。反之，越“远”或越“分散”，那么这组数据的方差和标准差就越大。

例如，有两组数据：[8,12,9,10,11,8,12]和[6,1,7,11,13,15,17]，虽然两组数据的均值都是10，但是前者的方差为3，后者的方差为31.66667。这也就是说前一组数据分布得较为“拥挤”，后一组数据分布得较为“分散”。

2.2 协方差及协方差矩阵

协方差度量的是特征与特征之间的关系。

例如我们收集到某地居民的身高，年龄，体重，胸宽，臂长的数据信息。对于这样的数据集，我们可以分别独立地计算出每一个特征数据的方差，但是我们如果还想知道这些特征之间的关系，就需要计算协方差。

对于都含有个数据的两组数据和,这两组数据的协方差计算公式为:

$cov(x,y)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1}$

协方差所刻画的是，两个变量在变化的过程中变化方向的一致性和变化大小的程度。

若变大也变大，即两个变量是同向变化的，此时协方差为正；反之为负。两者的变化趋势相互独立的时候，协方差为0。

方差主要是针对一维数据，协方差主要针对二维数据，那么多维数据的这种关系如何刻画呢？这个时候，协方差矩阵出场了。

协方差矩阵就是用来来那个多特征的两两之间协方差的矩阵。一般地，设有个特征，记为 $x_{1},x_{2},\cdots ,x_{n}$ ,那么这个特征的协方差矩阵为：

$\begin{Bmatrix} Cov(x_{1},x_{1}) &Cov(x_{1},x_{2}) &\cdots &Cov(x_{1},x_{n}) \\ Cov(x_{2},x_{1}) &Cov(x_{2},x_{2}) &\cdots &Cov(x_{2},x_{n}) \\ \vdots &\vdots &\ddots &\vdots \\ Cov(x_{n},x_{1})&Cov(x_{n},x_{2}) &\cdots &Cov(x_{n},x_{n}) \end{Bmatrix}$

由 $Cov(x_{i},x_{j})=Cov(x_{j},x_{i})$ 可知，协方差矩阵为实对称矩阵。再注意到，一组数据与它本身的协就是该组数据的方差，故协方差矩阵的主对角元分别是各个特征的方差。

2.3 向量在不同基下的坐标

基是线性空间的一个基本概念，其特点体现在以下两个方面：a.组成基的向量组线性无关;b.线性空间中的任何一个向量都可以由基线性表出。基是线性空间构成的基础，也就是说，基一旦确定了，那么线性空间也就确定了。

线性空间大家也不用想复杂了，就是一些向量构成的集合。

例如， $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 这个向量实际上是处于 $\begin{bmatrix} 1\\ 0\end{bmatrix}$ ， $\begin{bmatrix} 0\\ 1\end{bmatrix}$ 这组标准正交基（标准：每个向量模长都为1，正交：垂直/内积为0）所张成的空间中。 $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 在轴上的投影，实际上就是 $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 与 $\begin{bmatrix} 1\\ 0\end{bmatrix}$ 的内积值，即该投影值为 $\begin{bmatrix} 4\\ 3\end{bmatrix}\cdot \begin{bmatrix} 1\\ 0\end{bmatrix}=4$ 。同样， $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 在轴上的投影就是 $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 与 $\begin{bmatrix} 0\\ 1\end{bmatrix}$ 的内积，即该投影值为 $\begin{bmatrix} 4\\ 3\end{bmatrix}\cdot \begin{bmatrix} 0\\ 1\end{bmatrix}=3$ 。

上述的向量投影可以写成矩阵向量相乘的形式：

$\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}\begin{bmatrix} 4\\ 3\end{bmatrix}=\begin{bmatrix} 4\\ 3\end{bmatrix}$ 。

那么选择的基不同，相应向量的坐标也自然会不同。例如，如果选择两个标准正交向量 $\begin{bmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{bmatrix}$ 和 $\begin{bmatrix} \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\end{bmatrix}$ 作为基，那么 $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 这个向量在这两个向量所张成的空间中的坐标可以这样来考虑： $\begin{bmatrix} 4\\ 3\end{bmatrix}$

在向量 $\begin{bmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{bmatrix}$ 上的投影是两者的内积 $\begin{bmatrix} 4\\ 3\end{bmatrix}\cdot \begin{bmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{bmatrix}=\frac{7\sqrt{2}}{2}$ 。同样地， $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 在向量 $\begin{bmatrix} \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\end{bmatrix}$ 上的投影为 $\begin{bmatrix} 4\\ 3\end{bmatrix}\cdot \begin{bmatrix} \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\end{bmatrix}=\frac{\sqrt{2}}{2}$ ，即向量 $\begin{bmatrix} 4\\ 3\end{bmatrix}$ 在上述两向量做为基张成的空间中的坐标为 $\begin{bmatrix} \frac{2\sqrt{7}}{2}\\ \frac{\sqrt{2}}{2}\end{bmatrix}$ 。写成矩阵的形式就是：

$\begin{bmatrix} \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{bmatrix}\begin{bmatrix} 4\\ 3\end{bmatrix}=\begin{bmatrix} \frac{2\sqrt{7}}{2}\\ \frac{\sqrt{2}}{2}\end{bmatrix}$ 。

现在将上述结果推广到维的空间中：

对于任意维空间中的向量 $\alpha =\begin{bmatrix} x_{1} &x_{2} &\cdots &x_{m-1} &x_{m} \end{bmatrix}^{T}$ ,可以理解成其位于以个标准正交向量 $\begin{bmatrix} 1 &0 &0 &\cdots &0 \end{bmatrix}^{T},\begin{bmatrix} 0 &1 &0 &\cdots &0 \end{bmatrix}^{T},\cdots ,\begin{bmatrix} 0 &0 &0 &\cdots &1 \end{bmatrix}^{T}$ 为基底所张成的空间中，且其坐标分量就是其分别在这个维的标准正交向量上的投影值。可写成矩阵与向量相乘的形式：

$\begin{bmatrix} 1 &0 &0 &\cdots &0 \\ 0&1 &0 &\cdots &0 \\ 0&0 &1 &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &1 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \vdots \\ x_{m}\end{bmatrix}=\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \vdots \\ x_{m}\end{bmatrix}$ 。

所以，我们如果想将任意一个向量 $\alpha =\begin{bmatrix} x_{1} &x_{2} &\cdots &x_{m-1} &x_{m} \end{bmatrix}^{T}$ 变换到一个由个维的标准正交基向量所组成的新空间中，只需要将这( $k\leq m$ )个维的标准正交基向量以行向量的形式做成一个矩阵，然后将矩阵左乘向量 $\alpha$ 的原坐标即可得到 $\alpha$ 在新空间中的坐标。

2.4 矩阵乘法

在上面，我们说到对于任意一个向量 $\alpha =\begin{bmatrix} x_{1} &x_{2} &\cdots &x_{m-1} &x_{m} \end{bmatrix}^{T}$ ，要将其变换到以指定个数的标准正交向量的新空间中，只要将指定个数(比如指定个数为)的这些维的标准正交向量以行向量作成矩阵的样子，记为，拿这个东西左乘 $\alpha$ 可以了。

比如说，这个维的标准正交向量我们记为 $\beta _{1},\beta _{2},\cdots, \beta _{k}$ (这这些都是列向量)，那么要得到 $\alpha$ 在这组基张成的空间中的坐标，就可以这样来计算：

$\begin{bmatrix} \beta _{1}^{T}\\ \beta _{2}^{T}\\ \beta _{3}^{T}\\ \vdots \\ \beta _{k}^{T}\end{bmatrix}\alpha =\begin{bmatrix} \beta _{1}^{T}\alpha \\ \beta _{2}^{T}\alpha \\ \beta _{3}^{T}\alpha \\ \vdots \\ \beta _{k}^{T}\alpha \end{bmatrix}$ (注意：内积本质是一个实数)

上面仅仅知识针对一个向量作换，受到上述的启示我们容易发现，如果不止一个向量作变换，而是有个向量 $\alpha _{1},\alpha _{2},\cdots ,\alpha _{n}$ 也想作变换：

$\begin{bmatrix} \beta _{1}^{T}\\ \beta _{2}^{T}\\ \beta _{3}^{T}\\ \vdots \\ \beta _{k}^{T}\end{bmatrix}\begin{bmatrix} \alpha _{1} &\alpha _{2} &\alpha _{3} &\cdots &\alpha _{n} \end{bmatrix}=\begin{bmatrix} \beta _{1}^{T}\alpha _{1} &\beta _{1}^{T}\alpha _{2} &\beta _{1}^{T}\alpha _{3} &\cdots &\beta _{1}^{T}\alpha _{n} \\ \beta _{2}^{T}\alpha _{1}&\beta_{2}^{T}\alpha _{2} &\beta _{2}^{T}\alpha _{3} &\cdots &\beta _{2}^{T}\alpha _{n} \\ \beta _{3}^{T}\alpha _{1}&\beta _{3}^{T}\alpha _{2} &\beta _{3}^{T}\beta _{3} &\cdots &\beta _{3}^{T}\alpha _{n} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ \beta _{k}^{T}\alpha _{1} &\beta _{k}^{T}\alpha _{2} &\beta _{k}^{T}\alpha _{3} &\cdots &\beta _{k}^{T}\alpha _{n} \end{bmatrix}$

其中 $\beta _{j}$ 是标准正交的列向量， $\beta _{j}^{T}$ 是对应的行向量，表示第个基向量（ $j=1,2,\cdots ,k$ ）； $\alpha _{i}$ 表示的是第个需要变换的列向量（ $i=1,2,\cdots ,n$ ）。

我们在面对大数据集的时候，其实我们可以将数据集看作一个矩阵。这里，是一个不超过的正数，决定了通过降维以后得到的维度，即可以将维的数据 $\alpha _{i}$ 变换到更低维的空间中，变换后的维度取决于正整数。所以，矩阵相乘也可以表示降维变换。

通过上面的表述来看，矩阵相乘的几何意义就是：当左端矩阵行满秩时，两个矩阵相乘的结果就是将右端矩阵的列向量变换到左端矩阵的行向量为基底的新空间中。

2.5 矩阵的特征值和特征向量

特征值和特征向量是矩阵（或线性变换）的重要概念之一，有许多广泛的应用。

阶方阵的特征值和特征向量定义如下：

若有非零向量 $\alpha$ ，使得 $A\alpha =\lambda \alpha$ ，则 $\lambda$ 称为的特征值， $\alpha$ 称为属于特征值 $\lambda$ 的特征向量。

这里有2个重要的定理需要知道：（证明这里就不说了，相关内容可查线性代数的有关资料）

Theorem1:不同特征值的特征向量线性无关。

Theorem2:不用特征值的特征向量一定正交（内积为0）。

先知道这个东西是非常有必要的，因为降维的时候，低维的新空间的基其实就是原数据集矩阵去零均值化的矩阵的单位正交特征向量。此时此刻，你一定很好奇，先别急，继续往下看。

2.6 实对称矩阵正交相似于对角矩阵

上面说到了阶方阵的特征值和特征向量，如果级矩阵有个不同的特征值，分别记为 $\lambda _{1},\lambda _{2},\cdots ,\lambda _{n}$ ，那每一个特征值都有一个特征向量，故有个特征向量，对应地分别记为 $\beta _{1},\beta _{2},\cdots ,\beta _{n}$ ，那么根据特征值特征向量的定义，必然有 $A\beta _{i}=\lambda _{i}\beta _{i}$ ， $i=1,2,\cdots ,n$ ，写成矩阵乘积的样子，就是

$A\begin{bmatrix} \beta _{1} &\beta _{2} &\cdots &\beta _{n} \end{bmatrix}=\begin{bmatrix} \beta _{1} &\beta _{2} &\cdots &\beta _{n} \end{bmatrix}\begin{bmatrix} \lambda _{1} &0 &0 &\cdots &0 \\ 0&\lambda _{2} &0 &\cdots &0 \\ 0&0 &\lambda _{3} &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &\lambda _{n} \end{bmatrix}$ ，

而根据Theorem1, $\beta _{1},\beta _{2},\cdots ,\beta _{n}$ 线性无关，故矩阵 $\begin{bmatrix} \beta _{1} &\beta _{2} &\cdots &\beta _{n} \end{bmatrix}$ 满秩（可逆），记为，故上述式子可以写成

$P^{-1}AP=\begin{bmatrix} \lambda _{1} &0 &0 &\cdots &0 \\ 0&\lambda _{2} &0 &\cdots &0 \\ 0&0 &\lambda _{3} &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &\lambda _{n} \end{bmatrix}$ 。

对于实对称矩阵，它有较好的性质，定理表述如下：

Theorem3:设是级实对称矩阵， $\lambda _{1},\lambda _{2},\cdots ,\lambda _{n}$ 是的实对称矩阵，则必存在正交矩阵使得：

$TAT^{-1}=\begin{bmatrix} \lambda _{1} &0 &0 &\cdots &0 \\ 0&\lambda _{2} &0 &\cdots &0 \\ 0&0 &\lambda _{3} &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &\lambda _{n} \end{bmatrix}$ ，

其中满足： $TT^{-1}=T^{-1}T=E$ ，也就说，上述的列向量是由的个单位特征向量构成的矩阵。

关于上述定理的证明此处就不在给出，想了解给多的读者可查询线性代数有关资料。

3 PCA降维的核心思想

（1）核心思想一：基变换向量投影

对于任何一个维的向量 $\alpha$ ，如果要想将它投影到低维（ $k,k\leq m$ ）的空间中，我们可以利用维空间的一组标准正交基以行向量的形式组成的矩阵，然后将左乘向量 $\alpha$ 即可得到投影结果。

刚刚说的只是单个维向量的情况，那如果是多个维向量 $\alpha _{1},\alpha _{2},\cdots ,\alpha _{n}$ 也想降维，我们也可以作同样的处理，设降到低维目标空间的标准正交基分别是 $\varepsilon _{1},\varepsilon _{2},\cdots ,\varepsilon _{k}$ ，那么降维处理如下进行：

$\begin{bmatrix} \varepsilon _{1}^{T}\\ \varepsilon _{2}^{T}\\ \varepsilon _{3}^{T}\\ \vdots \\ \varepsilon _{k}^{T}\end{bmatrix}\begin{bmatrix} \alpha _{1} &\alpha _{2} &\alpha _{3} &\cdots &\alpha _{n} \end{bmatrix}=\begin{bmatrix} \varepsilon _{1}^{T}\alpha _{1} &\varepsilon _{1}^{T}\alpha _{2} &\varepsilon _{1}^{T}\alpha _{3} &\cdots &\varepsilon _{1}^{T}\alpha _{n} \\ \varepsilon _{2}^{T}\alpha _{1} &\varepsilon _{2}^{T}\alpha _{2} &\varepsilon _{2}^{T}\alpha _{3} &\cdots &\varepsilon _{2}^{T}\alpha _{n} \\ \varepsilon _{3}^{T}\alpha _{1} &\varepsilon _{3}^{T}\alpha _{2} &\varepsilon _{3}^{T}\alpha _{3} &\cdots &\varepsilon _{3}^{T}\alpha _{n} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ \varepsilon _{k}^{T}\alpha _{1} &\varepsilon _{k}^{T}\alpha _{2} &\varepsilon _{k}^{T}\alpha _{3} &\cdots &\varepsilon _{k}^{T}\alpha _{n} \end{bmatrix}$

所得结果的矩阵中，每一个列向量都是降维后的结果，也就是投影到低维目标空间中的结果。

（2）核心思想二：协方差归零投影

我们作数据降维，希望将原始数据的特征维度降低，同时又要尽可能的减少原始数据的信息损失。要在上述两点之间找到一个平衡点可不是意见容易的事儿。

仔细想一想，降维后的数据应该具备这样的特点：

各个维度之间的关联度尽可能的低，因为有关联的每一个组，我们只希望留下一个，其余的删除以降低数据集的复杂度。从协方差上来看，也就是降维后的特征两两之间的协方差为0是最好的，即降维后的数据集其协方差矩阵非对角上的元素全为0，这样的降维投影才是我们想要的。

（3）核心思想三：最大方差投影

我们平时对三维空间的物体拍照时，实际上就是将三维空间的物体投影到二维空间。我们先来观察一组拍摄笔筒的照片：

图3-1

笔筒是三维空间中的立体，照片是二维空间中的平面，从立体到平面的过程中肯定会失真（丢失信息），但是，不同的投影方式（拍摄角度）失真的程度不相同。如图3-1，三张图片都是拍摄同一个笔筒，但是由于拍摄角度的不同，第三张图片最大程度地保留了三维空间中笔筒的“重要信息”。

同理，我们在对数据作降维处理的时候，希望投影的方式能够使得降维后的数据尽可能的“分散”，这样可以使得我们尽可能地减小由于降维带来的信息损失，也就说，希望各个特征数据的方差尽可能地大。

4 PCA降维的原理

对数据作投影变换，实际上就是要找到要变换到一组目标新空间的标准正交基，将其以行向量作成一个矩阵，然后左乘数据矩阵即可实现降维，问题的关键在于，如何根据已知的大数据集和和需要降到的新空间的维度去找到这样的矩阵。

这里我们需要特别注意的是，我们要删除的是部分特征数据，根据前面所讲的基变换向量投影的原理，我们最后降下来的是原来数据集的行特征。因此，左乘矩阵相当于减少了原来数据集的行特征。如果我们要删除的列特征，那就用的转置右乘数据集矩阵或者用左乘数据集矩阵的转置即可。

下面讨论如何按照要求找的问题：

4.1 PCA降维具体例子示范

在这之前，先以一个具体例子来说明，下表（表4-1）是摘自于2021年举行的“华为杯”研究生数学建模竞赛B题的数据中的监测点A的污染物浓度，包含6个特征数据，共有9个数据样本。

表4-1

监测日期	SO2监测浓度(μg/m³)	NO2监测浓度(μg/m³)	PM10监测浓度(μg/m³)	PM2.5监测浓度(μg/m³)	O3最大八小时滑动平均监测浓度(μg/m³)	CO监测浓度(mg/m³)
2021/4/1	2	12	25	7	51	0.6
2021/4/2	4	17	29	12	61	0.7
2021/4/3	7	25	40	18	88	0.8
2021/4/4	4	25	49	21	47	1
2021/4/5	4	32	52	28	67	1.1
2021/4/6	6	43	82	49	259	1.2
2021/4/7	4	23	48	27	122	0.9
2021/4/8	3	36	33	15	67	0.9
2021/4/9	4	41	35	18	51	1.1

原数据集有6个特征数据，现在希望能够降到3维，

为了方便计算展示，将特征数据零均值化（每一个污染物浓度数据减去对应污染物浓度数据值）如表4-2所示：

表4-2

SO2监测浓度(μg/m³)	NO2监测浓度(μg/m³)	PM10监测浓度(μg/m³)	PM2.5监测浓度(μg/m³)	O3最大八小时滑动平均监测浓度(μg/m³)	CO监测浓度(mg/m³)
-2.22222	-16.2222	-18.6667	-14.6667	-39.3333	-0.32222
-0.22222	-11.2222	-14.6667	-9.66667	-29.3333	-0.22222
2.777778	-3.22222	-3.66667	-3.66667	-2.33333	-0.12222
-0.22222	-3.22222	5.333333	-0.66667	-43.3333	0.077778
-0.22222	3.777778	8.333333	6.333333	-23.3333	0.177778
1.777778	14.77778	38.33333	27.33333	168.6667	0.277778
-0.22222	-5.22222	4.333333	5.333333	31.66667	-0.02222
-1.22222	7.777778	-10.6667	-6.66667	-23.3333	-0.02222
-0.22222	12.77778	-8.66667	-3.66667	-39.3333	0.177778

#上述计算过程的代码：

import pandas as pd
import numpy as np
data=pd.read_excel('F:\\研究生生涯\\基于Python的机器学习实践\\Python统计建模——多元分析\\主成分分析\\监测点A的污染物浓度.xlsx')
data1=data.iloc[:,2:8]   #提取特征数据
print(data1)
y=data1.mean(axis=0)
new_data=data1-y
print(new_data)
new_data.to_excel('F:\\研究生生涯\\基于Python的机器学习实践\\Python统计建模——多元分析\\主成分分析\\new_data1.xlsx',index=False)

将上述经过零均值化的数据记为矩阵,

第一步，计算的6个列向量（各污染物浓度，分别是 $SO_{2},NO_{2},PM10,PM2.5,O_{3},CO$ ）的协方差矩阵:

$C=\frac{1}{6-1}A^{T}A=\frac{1}{5}A^{T}A$

利用程序计算得到A的列向量的协方差矩阵为：

[[2.19444444e+00 5.56944444e+00 1.42083333e+01 9.95833333e+00
5.40416667e+01 1.06944444e-01]
[5.56944444e+00 1.11694444e+02 1.05458333e+02 8.27083333e+01
3.33666667e+02 1.85694444e+00]
[1.42083333e+01 1.05458333e+02 2.94000000e+02 2.06500000e+02
9.92500000e+02 2.60833333e+00]
[9.95833333e+00 8.27083333e+01 2.06500000e+02 1.49500000e+02
7.28625000e+02 1.92083333e+00]
[5.40416667e+01 3.33666667e+02 9.92500000e+02 7.28625000e+02
4.54725000e+03 6.45416667e+00]
[1.06944444e-01 1.85694444e+00 2.60833333e+00 1.92083333e+00
6.45416667e+00 3.94444444e-02]]

#程序代码：

Cov=new_data.cov()
Cov_mat=np.mat(Cov)  #转化为矩阵
print(Cov_mat)

第二步，计算上述协方差矩阵的特征值和特征向量：

特征值: [4.91534585e+03 1.33082140e+02 5.29262797e+01 1.96958266e+00 1.35401494e+00 4.69063054e-04]

单位特征向量(按列):

[[-0.0115945 0.01982138 -0.00887949 0.44895534 0.89318819 0.00691333]
[-0.07419199 0.63756657 0.75938908 0.09150018 -0.05347679 -0.01002928]
[-0.21512829 0.59755921 -0.59197066 0.43419812 -0.2401709 -0.00186604]
[-0.15753526 0.41548756 -0.24453222 -0.77527456 0.37611186 -0.01568266]
[-0.96086494 -0.2513976 0.11409595 0.01743293 -0.01453903 0.00215488]
[-0.00146569 0.01443296 0.0024926 -0.01357453 -0.00122989 0.99979875]]

#计算的程序代码为

eige,feat=np.linalg.eig(Cov_mat)
print('特征值:',eige)
print('单位特征向量(按列):',feat)

现在我们希望降到3维，那我们就选择特征值按照从大到小排序的前三个特征值所对应的三个单位特征向量以列向量作成矩阵右乘矩阵即可实现降维。

最大的三个特征值分别为：4915.345846940669, 133.08213998288508, 52.92627974504706，即前三个特征向量，

第一个特征值4915.345846940669对应的特征向量为：

[[-0.0115945 ]
[-0.07419199]
[-0.21512829]
[-0.15753526]
[-0.96086494]
[-0.00146569]]

第二个特征值133.08213998288508对应的特征向量为：

[[ 0.01982138]
[ 0.63756657]
[ 0.59755921]
[ 0.41548756]
[-0.2513976 ]
[ 0.01443296]]

第三个特征值52.92627974504706对应的特征值为：

[[ 0.01982138]
[ 0.63756657]
[ 0.59755921]
[ 0.41548756]
[-0.2513976 ]
[ 0.01443296]]

#抽取特征值的程序：

f1=feat[:,0]
f2=feat[:,1]
f3=feat[:,2]
print('f1:',f1)
print('f2:',f2)
print('f2:',f2)

第三步，矩阵相乘实现降维：

将上述的三个单位特征列向量就以列的形式作成矩阵，得到的是一个6行3列的矩阵，如：

=[[-0.0115945 0.01982138 -0.00887949]
[-0.07419199 0.63756657 0.75938908]
[-0.21512829 0.59755921 -0.59197066]
[-0.15753526 0.41548756 -0.24453222]
[-0.96086494 -0.2513976 0.11409595]
[-0.00146569 0.01443296 0.0024926]]

#程序代码：

Q=feat[:,0:3]
print(Q)

然后将右乘矩阵即可实现降维：

[[ 45.35006284 -17.75139542 -2.15123174]
[ 33.6989285 -12.56877783 -0.82138033]
[ 3.81548648 -5.12899626 0.32906309]
[ 40.83667895 11.74622317 -10.38306642]
[ 19.351758 15.88377111 -6.27281217]
[-175.73584671 1.32176622 1.07508344]
[ -31.80974419 -6.48980673 -4.22012044]
[ 25.20227352 1.65636615 11.19948665]
[ 39.2904026 11.33084959 11.24497794]]

#计算的程序代码：

A=np.mat(new_data)   #dataframe转化成为矩阵，以便于实现矩阵乘法运算
result=A*Q
print(result)

综合来看，PCA数据降维的过程可以按照如下步骤进行：

1.计算原矩阵的协方差矩阵C;

2.计算协方差矩阵C的特征值和特征向量；

3.选择最大的个特征值对应的特征向量组成降维矩阵；

4.将降维矩阵乘矩阵即可实现PCA降维。

下面来看究竟是为什么？我们要这样做：

4.2 PCA降维原理分析

从上面我们已经知道，对大数据集作降维变换的实质就是找到一个矩阵与原矩阵（零均值化的数据与原数据在信息上是等价的）作矩阵乘法即可实现降维。

设是方阵（先不考虑降维），记。是 $n\times m$ 的原数据零均值化的矩阵，是 $m\times m$ 矩阵，是矩阵相乘的结果（或者线性变换的结果），是 $n\times m$ 矩阵，我们应该按照我们降维的要求去寻找降维矩阵 $Q_{m\times k}$ 。

计算矩阵乘积的结果的协方差矩阵 $C_{y}$ :

$C_{y}=$ $\frac{1}{m-1}Y^{T}Y$

由于，故

$C_{y}=\frac{1}{m-1}(AP)^{T}(AP)=\frac{1}{m-1}P^{T}A^{T}AP=P^{T}(\frac{1}{m-1}A^{T}A)P=P^{T}CP$

即 $C_{y}=P^{T}CP$ 。 $C_{m\times m}$ 是的个列特征的协方差矩阵,不要忘了协方差矩阵是对角矩阵！

我们说，降维后，应该数据特征尽量相关性低，或者不具有相关性，这个样子是最好的。什么意思？也就是说，不同特征的协方差希望是0，这个时候达到的效果最好。从协方差矩阵的角度来看，就是说的协方差矩阵是对角矩阵的话就非常完美了。

的协方差矩阵 $C_{y}=P^{T}CP$ ，回忆前述的Theorem3，要使得 $C_{y}$ 为对角矩阵，那只要是的个单位特征向量以列组成的正交矩阵即可。不妨设 $C_{m\times m}$ 的特征值分别是 $\lambda _{1},\lambda _{2},\cdots ,\lambda _{m}$ ，对应的单位特征向量分别是 $\beta _{1},\beta _{2},\cdots ,\beta _{m}$ ，那么写出来写出就是

$C_{y}=\begin{bmatrix} \lambda _{1} &0 &0 &\cdots &0 \\ 0&\lambda _{2} &0 &\cdots &0 \\ 0&0 &\lambda _{3} &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &\lambda _{m}\end{bmatrix}=\begin{bmatrix} \beta _{1} &\beta _{2} &\beta _{3} &\cdots &\beta _{m} \end{bmatrix}^{T}C\begin{bmatrix} \beta _{1} &\beta _{2} &\beta _{3} &\cdots &\beta _{m} \end{bmatrix}$

另外还有一个要求：投影（降维）了以后，留下的各个特征自己要尽量“分散”，不要太“拥挤”，这样可以在最大程度上减少由于数据降维带来的信息损失，意思是每一个降维后留下的特征数据方差尽量大，而降维后每一个特征的方差就体现在协方差矩阵的对角线上。

所以，如果我们想将原数据集的行向量降成维（剔除部分在列位置上的特征数据），那么挑最大的个特征值对应的特征向量组成降维矩阵 $Q_{m\times k}$ ，拿去右乘原矩阵即可实现降维。

比如说，最大的个特征值是 $\lambda _{1},\lambda _{2},\cdots ,\lambda _{k}$ ，对应的特征向量分别是 $\beta _{1},\beta _{2},\cdots ,\beta _{k}$ ， $k\leq m$ ，那么降维矩阵就应该长成这样：

$Q=\begin{bmatrix} \beta _{1} &\beta _{2} &\beta _{3} &\cdots &\beta _{k} \end{bmatrix}$

然后将拿去右乘：

$Y^{'}=AQ$

得到降维后的数据矩阵 $Y^{'}$ ，

显然， $Y^{'}$ 的协方差矩阵就是

$\begin{bmatrix} \lambda _{1} &0 &0 &\cdots &0 \\ 0&\lambda _{2} &0 &\cdots &0 \\ 0&0 &\lambda _{3} &\cdots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&0 &0 &\cdots &\lambda _{k}\end{bmatrix}$

得到的这个数据 $Y^{'}$ ，实现了在降低大数据集的复杂度的同时，也最大程度上地减少了由于数据特征减少而带来的信息损失。其实质就是将数据的行向量投影到，以特征数据协方差矩阵的最大的个特征值对应的特征向量为基底的空间中。

我们可以总结一下PCA降维的步骤：

a.计算原矩阵的协方差矩阵;

b.计算的特征值特征向量；

c.拎出的（ $k\leq m$ ）个最大的特征值对应的特征向量 $\beta _{1},\beta _{2},\cdots ,\beta _{k}$ ；

d.将这个特征向量单位化了以后按列作成降维矩阵；

e.最后拿去右乘原矩阵即可。

好啦，接下来我们用Python的机器学习sklearn库来进行PCA降维的示范：

5 Python实现PCA降维

为了方便，采用sklearn库中自带的鸢尾花数据集（iris）来进行PCA算法的实现：

该数据集共有150个样本数据，每一个样本都有4个特征，分别是花萼长度、花萼宽度、花瓣长度、花瓣宽度，即该数据集的特征维度是4维的，有3类对鸢尾花分类的标签。

那么这些特征数据是否存在数据冗余？或者说怎么样合理地降低该数据集的特征维度？这里我们可以用PCA降维的方法来对鸢尾花数据集进行降维处理，从而熟悉PCA降维的原理和效果。因此，我们的目标就是，利用PCA降维的方法对鸢尾花的特征数据（4维）进行降维。

导入需要用的包：

#导入需要的包
from sklearn import datasets,decomposition
import numpy as np
import matplotlib.pyplot as plt

加载数据集并提取特征数据

iris=datasets.load_iris()
data=iris.data

查看数据维度情况：

print(data[0:5])

运行结果：

[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]

说明原数据的确是4维的。

根据方差（线性变换后数据的特征值）的占比情况确定合适的降维维度:

exv=pca.explained_variance_ratio_   #计算可解释方差占比
print('方差占比情况:',exv)

运行结果：方差占比情况: [0.92461872 0.05306648 0.01710261 0.00521218]

从结果来看，前两个特征比较显著，因此可以考虑降为2维：

new_pca=decomposition.PCA(n_components=2)  #设置k=2
new_pca.fit(data)   #训练数据
new_data=new_pca.transform(data)  #返回降维后的数据
print(new_data[0:5])

运行结果：

[[-2.68412563 0.31939725]
[-2.71414169 -0.17700123]
[-2.88899057 -0.14494943]
[-2.74534286 -0.31829898]
[-2.72871654 0.32675451]]

结果表明，的确从4维降到了2维。

print('降维后各个主成分的方差大小:',new_pca.explained_variance_)
print('降维后各个主成分的方差占比大小:',new_pca.explained_variance_ratio_)

运行结果：

降维后各个主成分的方差大小: [4.22824171 0.24267075]
降维后各个主成分的方差占比大小: [0.92461872 0.05306648]

好啦，就说到这里，望各位大佬指教！

你可能感兴趣的:(笔记,python,线性代数,算法,矩阵,机器学习)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
拥有断舍离的心态，过精简生活--《断舍离》读书笔记爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多，虽然摆放整齐，但也时常会觉得空间逼仄，令人心生烦闷。抱着断舍离的态度，我开始阅读《断舍离》这本书，希望从书中能找到一些有效的方法，帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的，整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”，接着又成为每个人都能实行的“改变人生的断舍离”，从“哲学”逐渐升华成“
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day17笔记-高阶函数 ~在杰难逃~ Python 笔记 python 开发语言 pycharm 数据分析
高阶函数【重点掌握】函数的本质：函数是一个变量，函数名是一个变量名，一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数，B函数调用完成之后，会得到一个结果，则B函数被称为高阶函数常用的高阶函数：map(),reduce(),filter(),sorted()1.map()map(func,iterable)，返回值是一个iterator【容器，迭代器】func:函数iterab
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
node.js学习小猿L node.js node.js 学习 vim
node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
PHP，安卓，UI，java，linux视频教程合集 cocos2d-x小菜 java UI PHP android linux
╔-----------------------------------╗┆
各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。 bozch .net .net mvc
在.net mvc5中，在执行某一操作的时候，出现了如下错误：各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。经查询当前的操作与错误内容无关，经过对错误信息的排查发现，事故出现在数据库迁移上。回想过去：在迁移之前已经对数据库进行了添加字段操作，再次进行迁移插入XXX字段的时候，就会提示如上错误。 &
Java 对象大小的计算 e200702084 java
Java对象的大小如何计算一个对象的大小呢？
Mybatis Spring 171815164 mybatis
ApplicationContext ac = new ClassPathXmlApplicationContext("applicationContext.xml"); CustomerService userService = (CustomerService) ac.getBean("customerService"); Customer cust
JVM 不稳定参数 g21121 jvm
-XX 参数被称为不稳定参数，之所以这么叫是因为此类参数的设置很容易引起JVM 性能上的差异，使JVM 存在极大的不稳定性。当然这是在非合理设置的前提下，如果此类参数设置合理讲大大提高JVM 的性能及稳定性。可以说“不稳定参数”
用户自动登录网站永夜-极光用户
1.目标:实现用户登录后,再次登录就自动登录,无需用户名和密码 2.思路:将用户的信息保存为cookie 每次用户访问网站,通过filter拦截所有请求,在filter中读取所有的cookie,如果找到了保存登录信息的cookie,那么在cookie中读取登录信息,然后直接
centos7 安装后失去win7的引导记录程序员是怎么炼成的操作系统
1.使用root身份(必须)打开 /boot/grub2/grub.cfg 2.找到 ### BEGIN /etc/grub.d/30_os-prober ### 在后面添加 menuentry "Windows 7 (loader) (on /dev/sda1)" {
Oracle 10g 官方中文安装帮助文档以及Oracle官方中文教程文档下载 aijuans oracle
Oracle 10g 官方中文安装帮助文档下载：http://download.csdn.net/tag/Oracle%E4%B8%AD%E6%96%87API%EF%BC%8COracle%E4%B8%AD%E6%96%87%E6%96%87%E6%A1%A3%EF%BC%8Coracle%E5%AD%A6%E4%B9%A0%E6%96%87%E6%A1%A3 Oracle 10g 官方中文教程
JavaEE开源快速开发平台G4Studio_V3.2发布了無為子 AOP oracle mysql javaee G4Studio
我非常高兴地宣布,今天我们最新的JavaEE开源快速开发平台G4Studio_V3.2版本已经正式发布。大家可以通过如下地址下载。访问G4Studio网站 http://www.g4it.org G4Studio_V3.2版本变更日志功能新增 (1).新增了系统右下角滑出提示窗口功能。 (2).新增了文件资源的Zip压缩和解压缩
Oracle常用的单行函数应用技巧总结百合不是茶日期函数转换函数(核心)数字函数通用函数(核心)字符函数
单行函数; 字符函数,数字函数,日期函数,转换函数(核心),通用函数(核心) 一:字符函数: .UPPER(字符串) 将字符串转为大写 .LOWER (字符串) 将字符串转为小写 .INITCAP(字符串) 将首字母大写 .LENGTH (字符串) 字符串的长度 .REPLACE(字符串,'A','_') 将字符串字符A转换成_
Mockito异常测试实例 bijian1013 java 单元测试 mockito
Mockito异常测试实例： package com.bijian.study; import static org.mockito.Mockito.mock; import static org.mockito.Mockito.when; import org.junit.Assert; import org.junit.Test; import org.mockito.
GA与量子恒道统计 Bill_chen JavaScript 浏览器百度 Google 防火墙
前一阵子，统计**网址时，Google Analytics（GA）和量子恒道统计（也称量子统计），数据有较大的偏差，仔细找相关资料研究了下，总结如下：为何GA和量子网站统计（量子统计前身为雅虎统计）结果不同？首先：没有一种网站统计工具能保证百分之百的准确出现该问题可能有以下几个原因：（1）不同的统计分析系统的算法机制不同；（2）统计代码放置的位置和前后
【Linux命令三】Top命令 bit1129 linux命令
Linux的Top命令类似于Windows的任务管理器，可以查看当前系统的运行情况，包括CPU、内存的使用情况等。如下是一个Top命令的执行结果： top - 21:22:04 up 1 day, 23:49, 1 user, load average: 1.10, 1.66, 1.99 Tasks: 202 total, 4 running, 198 sl
spring四种依赖注入方式白糖_ spring
平常的java开发中，程序员在某个类中需要依赖其它类的方法，则通常是new一个依赖类再调用类实例的方法，这种开发存在的问题是new的类实例不好统一管理，spring提出了依赖注入的思想，即依赖类不由程序员实例化，而是通过spring容器帮我们new指定实例并且将实例注入到需要该对象的类中。依赖注入的另一种说法是“控制反转”，通俗的理解是：平常我们new一个实例，这个实例的控制权是我
angular.injector boyitech AngularJS AngularJS API
angular.injector 描述: 创建一个injector对象, 调用injector对象的方法可以获得angular的service, 或者用来做依赖注入. 使用方法: angular.injector(modules, [strictDi]) 参数详解: Param Type Details mod
java-同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待 bylijinnan Integer
public class PC { /** * 题目：生产者-消费者。 * 同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待。 */ private static final Integer[] val=new Integer[10]; private static
使用Struts2.2.1配置 Chen.H apache spring Web xml struts
Struts2.2.1 需要如下 jar包: commons-fileupload-1.2.1.jar commons-io-1.3.2.jar commons-logging-1.0.4.jar freemarker-2.3.16.jar javassist-3.7.ga.jar ognl-3.0.jar spring.jar struts2-core-2.2.1.jar struts2-sp
[职业与教育]青春之歌 comsci 教育
每个人都有自己的青春之歌............但是我要说的却不是青春... 大家如果在自己的职业生涯没有给自己以后创业留一点点机会,仅仅凭学历和人脉关系,是难以在竞争激烈的市场中生存下去的.... &nbs
oracle连接(join)中使用using关键字 daizj JOIN oracle sql using
在oracle连接(join)中使用using关键字 34. View the Exhibit and examine the structure of the ORDERS and ORDER_ITEMS tables. Evaluate the following SQL statement: SELECT oi.order_id, product_id, order_date FRO
NIO示例 daysinsun nio
NIO服务端代码： public class NIOServer { private Selector selector; public void startServer(int port) throws IOException { ServerSocketChannel serverChannel = ServerSocketChannel.open(
C语言学习homework1 dcj3sjt126com c homework
0、课堂练习做完 1、使用sizeof计算出你所知道的所有的类型占用的空间。 int x; sizeof(x); sizeof(int); # include <stdio.h> int main(void) { int x1; char x2; double x3; float x4; printf(&quo
select in order by , mysql排序 dcj3sjt126com mysql
If i select like this: SELECT id FROM users WHERE id IN(3,4,8,1); This by default will select users in this order 1,3,4,8, I would like to select them in the same order that i put IN() values so:
页面校验-新建项目 fanxiaolong 页面校验
$(document).ready( function() { var flag = true; $('#changeform').submit(function() { var projectScValNull = true; var s =""; var parent_id = $("#parent_id").v
Ehcache（02）——ehcache.xml简介 234390216 ehcache ehcache.xml 简介
ehcache.xml简介 ehcache.xml文件是用来定义Ehcache的配置信息的，更准确的来说它是定义CacheManager的配置信息的。根据之前我们在《Ehcache简介》一文中对CacheManager的介绍我们知道一切Ehcache的应用都是从CacheManager开始的。在不指定配置信
junit 4.11中三个新功能 jackyrong java
junit 4.11中两个新增的功能，首先是注解中可以参数化，比如 import static org.junit.Assert.assertEquals; import java.util.Arrays; import org.junit.Test; import org.junit.runner.RunWith; import org.junit.runn
国外程序员爱用苹果Mac电脑的10大理由 php教程分享 windows PHP unix Microsoft perl
Mac 在国外很受欢迎，尤其是在设计/web开发/IT 人员圈子里。普通用户喜欢 Mac 可以理解，毕竟 Mac 设计美观，简单好用，没有病毒。那么为什么专业人士也对 Mac 情有独钟呢？从个人使用经验来看我想有下面几个原因： 1、Mac OS X 是基于 Unix 的这一点太重要了，尤其是对开发人员，至少对于我来说很重要，这意味着Unix 下一堆好用的工具都可以随手捡到。如果你是个 wi
位运算、异或的实际应用 wenjinglian 位运算
一．位操作基础，用一张表描述位操作符的应用规则并详细解释。二．常用位操作小技巧，有判断奇偶、交换两数、变换符号、求绝对值。三．位操作与空间压缩，针对筛素数进行空间压缩。 &n
weblogic部署项目出现的一些问题（持续补充中……） Everyday都不同 weblogic部署失败
好吧，weblogic的问题确实…… 问题一： org.springframework.beans.factory.BeanDefinitionStoreException: Failed to read candidate component class: URL [zip:E:/weblogic/user_projects/domains/base_domain/serve
tomcat7性能调优（01） toknowme tomcat7
Tomcat优化： 1、最大连接数最大线程等设置 <Connector port="8082" protocol="HTTP/1.1" useBodyEncodingForURI="t
PO VO DAO DTO BO TO概念与区别 xp9802 java DAO 设计模式 bean 领域模型
O/R Mapping 是 Object Relational Mapping（对象关系映射）的缩写。通俗点讲，就是将对象与关系数据库绑定，用对象来表示关系数据。在O/R Mapping的世界里，有两个基本的也是重要的东东需要了解，即VO，PO。它们的关系应该是相互独立的，一个VO可以只是PO的部分，也可以是多个PO构成，同样也可以等同于一个PO（指的是他们的属性）。这样，PO独立出来，数据持