第二次周报9.25

感知机（Perceptron)

查了很多关于相关资料，发现只给公式结果不给推导过程，看得百思不得其解，导致自己踩了不少坑，现在把卡住的公式推导过程写下来，用来日后参考

本文省略定义，着重在于公式推导和代码实现

定义

感知机是二类分类的线性分类模型，w是权重，x是特征，b是偏置，目标是得到能将训练数据进行线性划分的超平面，也就是得到w和b。

公式推导

1、证明w为超平面法向量

两向量相乘为0，若两向量都不为0，则两向量垂直

2、损失函数推理过程

为了对模型进行判断，我们要构建损失函数，往往就会想到以 被错误分类的点的数目 作为判断的标准

我们需要对损失函数进行优化，也就是找到极小值，来满足错误点总量最低，但有图可知，该函数不可导，所以我们不选择 错误点总量 作为损失函数

最终选择 所有错误点到超平面的距离之和 作为损失函数，推导公式如下（使用向量投影公式进行说明）：

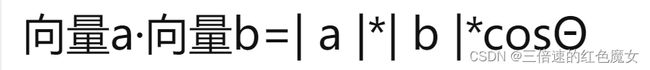
设x2为误分类的点，现求x2到超平面的距离，就要把x2投影到法向量上，推导过程如下：（这里|w|与二范数结果一样，本质都是向量内积）

进一步化简 开括号把w乘进去
有了绝对值之后，在x=0处不可导（参考y=|x|图像，左右导数不相等），所以进一步优化去绝对值
由错误点的性质可得 -yi(w*xi+b)>0
优化结果：

损失函数（错误点到超平面的距离之和）：

以上，推到完毕

3、学习策略

使用梯度下降法，不断的迭代更新w,b，找到最小值，直到不会出现误分类的点。

代码实现

#step1 加载鸢尾花数据集 并进行处理
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

iris = load_iris()
X = iris.data[:,2:4] # 选择3，4行作为两个特征 此处也可以写 X = iris.data[:,（2，3）]
# 把多分类转为2分类问题
Y = [1 if i == 0 else -1 for i in iris.target ] # 当target为0 类别设为1 其余为-1

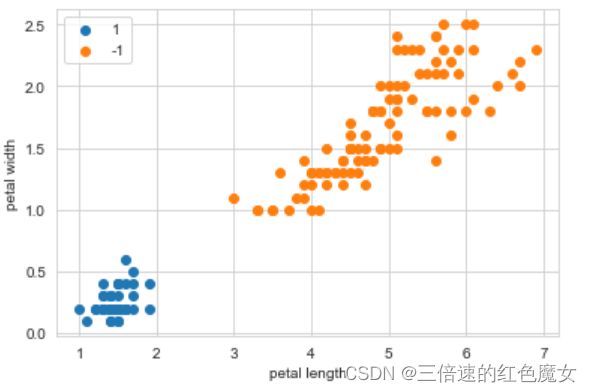
#对整理好的数据集做可视化处理
plt.scatter(X[:50,0], X[:50,1], label='1') # 前50个为1
plt.scatter(X[50:150,0], X[50:150,1],label='-1') #Y后100个为0类
plt.xlabel("petal length")
plt.ylabel("petal width")
plt.legend()#显示图例

# step2 定义感知机类 并封装属性和对应方法
class Peperceptron():
    
    def __init__(self,a,X,Y):
        self.w = np.zeros(len(X[0]),dtype=np.float) #权重 np.zeros返回一个（）内规定形状和数据类型，元素全为0的数组  
                                                # X是二维数组 X[0]是第一行  len(X[0]) = 2  self.w = [0,0]
        self.b = 0 #偏置
        self.a = a # 学习率
        self.X = X # 特征集
        self.Y = Y # 真实值
        self.iterTimes = 0 #迭代次数
    
    def sign(self,w,X,b):
        y = np.dot(w,X) + b # np.dot(a,b) a和b矩阵相乘
        return y
    def Gradient_descent(self): # 梯度下降法
        self.iterTimes = 0
        self.b = 0
        open = True
        while open:
            wrong_count = 0
            for i in range(len(self.X)):
                X = self.X[i]
                Y = self.Y[i]
                if Y * self.sign(self.w,X,self.b) <= 0:
                    self.w+= np.dot(Y,X)*self.a
                    self.b+= Y*self.a
                    
                    self.iterTimes+=1 #迭代次数+1
                    wrong_count+=1
            print("本轮有%d个错误点"%(wrong_count))
            if wrong_count == 0: # 直到循环一遍找不到任何一个错误点
                open = False
        print("算法完成，迭代次数为%d"%(self.iterTimes))   

调用梯度下降法的运行结果

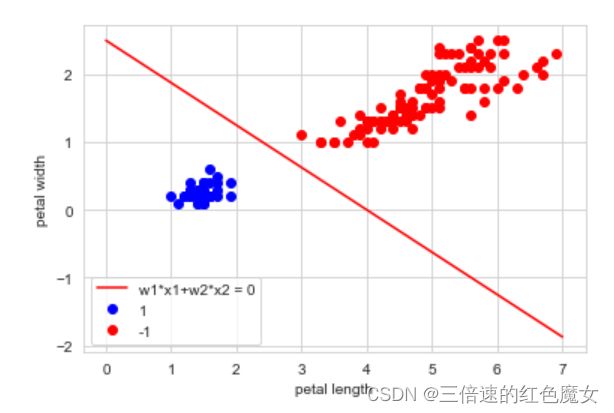
# 可视化结果
p = Peperceptron(0.3,X,Y) # 偏置 学习率 特征集 真实值
p.Gradient_descent()
x_points = np.linspace(0, 7, 10) # 随机在0-7区间上生成10个点作为x1
y0 = -(p.w[0] * x_points + p.b) / p.w[1] # 本质上是算x2
plt.plot(x_points, y0, 'r', label='w1*x1+w2*x2 = 0')

plt.plot(X[:50,0], X[:50,1],'bo', color="blue", label='1') # 前50个为+1类
plt.plot(X[50:150,0], X[50:150,1],'bo', color="red",label='-1') #后100个为-1类
plt.xlabel("petal length")
plt.ylabel("petal width")
plt.legend()#显示图例

阅读文献

现有研究方法

中文信息处理主要是对字、词、段落或篇章进行处理。
主要方法分别是基于规则和基于统计的方法
前者是人工根据语言相关的规则对文本进行处理；
后者则是通过大规模的数据库分析数据，从而实现对自然语言的处理。

自然语言处理受数据影响较大，而数据的增长是大多数 NLP 应用（如
机器翻译）性能提高的原因，所以拥有强大的数据支持才可
以更好的对文本进行进一步的理解和分析，这使得如今很多
NLP 应用程序采用数据流分析方法

潜在研究点

在最近阅读的文献中发现：许多实验在训练模型时可能会出现过拟合和欠拟合的状况。所谓过拟合就是学习到了噪声的数据特征，而欠拟合是不能较好的拟合数据。
解决的方法：过拟合的方法主要有增加正则化项从而增大数据的训练量，解决欠拟合则要减少正则化项，增加其他特征项处理数据。

总结

下周继续以学习nlp方向相关模型和算法为主，以便更快能够复现相关文献，并且继续读文献记录下潜在研究点和解决方法。