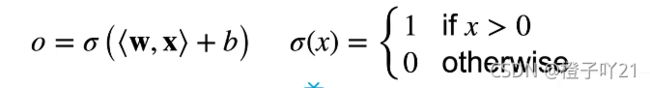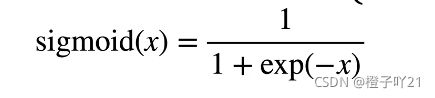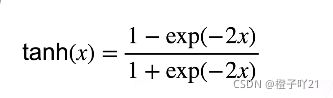动手学深度学习——多层感知机的激活函数及代码实现

感知机

给定输入x（向量），权重w（向量），和偏移b（标量），感知机输出：

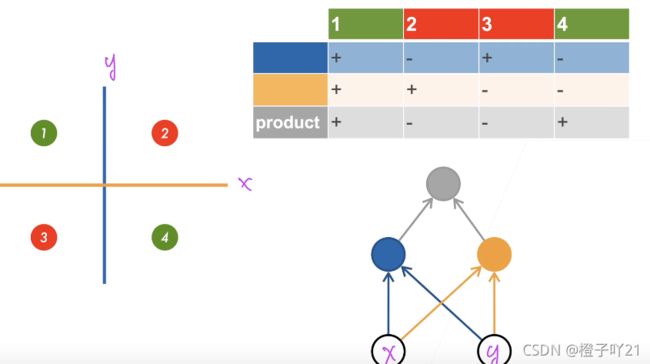
感知机不能拟合XOR函数，他只能产生线性分割面。

感知机是一个二分类的模型，是最早的AI模型之一。

感知机的求解算法等价于使用批量大小为1 的梯度下降。

多层感知机

1、学习XOR

 

2、单隐藏层-单分类

 

为什么需要非线性的激活函数？

如果不加激活函数，就是n个全连接层叠加在一起，输出还是一个最简单的线性模型。

3、激活函数

3.1 sigmoid 函数

他就是说对于x来讲，将他投影到（0,1）的开区间，就是如果x大于0，就是1；如果x小于0，就是0。它是跳跃函数，僵硬的。

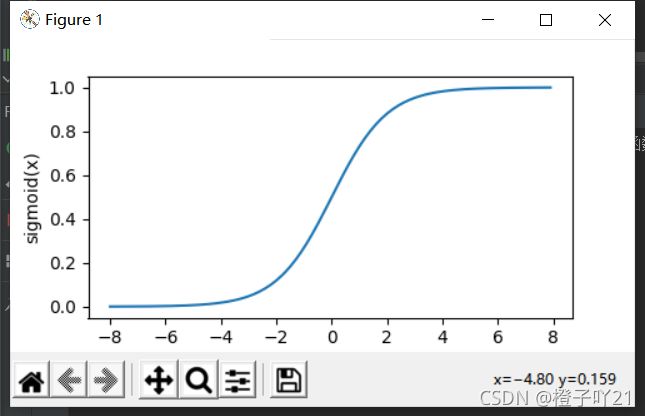
sigmoid函数就是将输入投影到（0,1）的开区间，它是曲线函数，软的光滑的。

# sigmoid函数

import torch
import numpy as np
import  matplotlib.pylab as plt
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l

def xypolt(x_vals,y_vals,name):
    d2l.set_figsize(figsize=(5,2.5))
    d2l.plt.plot(x_vals.detach().numpy(),y_vals.detach().numpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name+'(x)')
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
y=x.sigmoid()
xypolt(x,y,'sigmoid')
plt.show()

"""
求导实现
"""
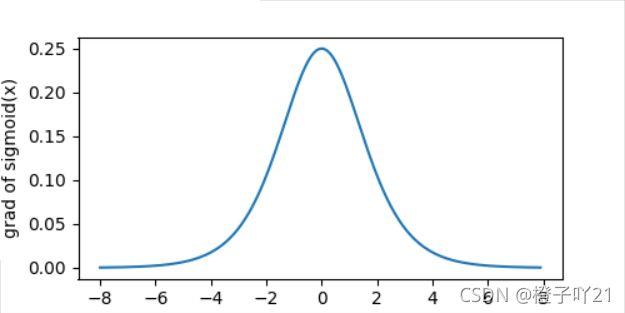
x.grad.zero_() #梯度清零
y.sum().backward() #进行求导
xypolt(x,x.grad,'grad of sigmoid')
plt.show()

 

 

3.2 tanh 函数

tanh （双曲正切）函数可以将元素的值变换到 -1 和 1 之间：

import torch
import numpy as np
import  matplotlib.pylab as plt
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l

def xypolt(x_vals,y_vals,name):
    d2l.set_figsize(figsize=(5,2.5))
    d2l.plt.plot(x_vals.detach().numpy(),y_vals.detach().numpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name+'(x)')
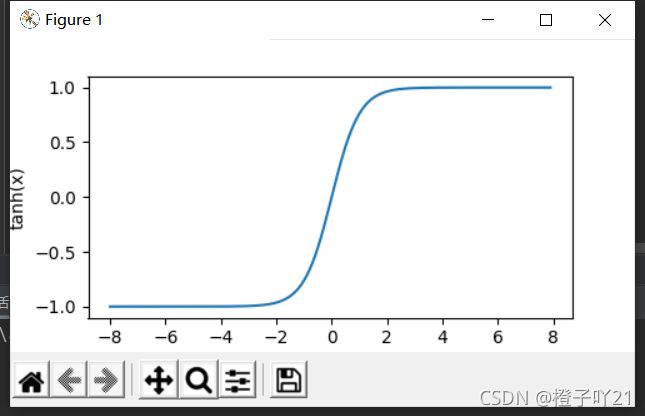
#tanh函数
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
y=x.tann()
xypolt(x,y,'tanh')
plt.show()

"""
求导实现
"""
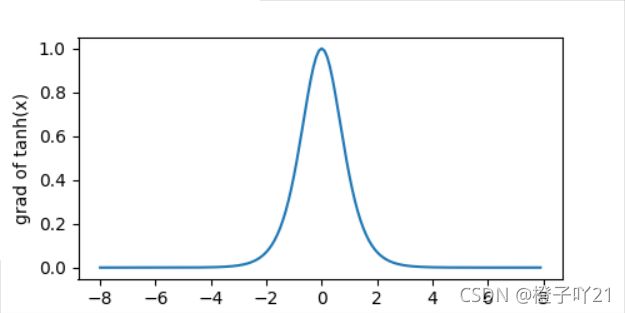
x.grad.zero_() #梯度清零
y.sum().backward() #进行求导
xypolt(x,x.grad,'grad of tanh')
plt.show()

 

 

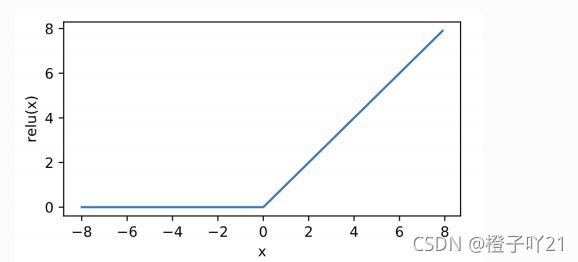
3.3 ReLU函数

ReLU （ rectified linear unit ）函数提供了⼀个很简单的⾮线性变换。给定元素 ，该函数定义为：

ReUL(x)=max(x,0)。

import torch
import numpy as np
import  matplotlib.pylab as plt
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l

def xypolt(x_vals,y_vals,name):
    d2l.set_figsize(figsize=(5,2.5))
    d2l.plt.plot(x_vals.detach().numpy(),y_vals.detach().numpy())
    d2l.plt.xlabel('x')
    d2l.plt.ylabel(name+'(x)')
#1、ReLU函数
"""
接下来利用NDArray提供的relu函数来绘制ReLU函数
"""
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
y=x.relu()
xypolt(x,y,'relu')
plt.show()

 

"""
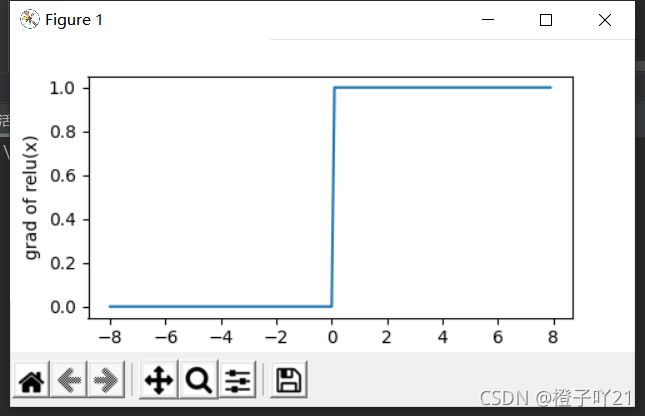
显然，当输入是负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1.尽管输入为0时ReLU函数不可导，
但我们可以取此处的导数为0，下面绘制ReLU函数的导数。
"""
x.grad.zero_() #梯度清零
y.sum().backward()
xypolt(x,x.grad,'grad of relu')
plt.show()

 

4、多层感知机

多层感知机就是含有⾄少⼀个隐藏层的由全连接层组成的神经⽹络，且每个隐藏层的输出通过激活函数 进⾏变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。

以单隐藏层为例并沿⽤本节之前 定义的符号，多层感知机按以下⽅式计算输出：

其中 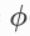表示激活函数。在分类问题中，我们可以对输出 做softmax运算，并使⽤ softmax 回归中的交叉 熵损失函数。 在回归问题中，我们将输出层的输出个数设为1 ，并将输出 直接提供给线性回归中使⽤ 的平⽅损失函数。

 5、总结

• 多层感知机使用隐藏层和激活函数来得到非线性模型。
• 常用的激活函数是Sigmoid、Tanh、ReLU。
• 使用Softmax来处理多分类。
• 超参数为隐藏层数和各个隐藏层大小。