二叉树的线索化（带有头结点与非头结点的区别）及其遍历 （超级详细）

线索二叉树

我们先来看一下什么是线索二叉树
我想平常的二叉树的结构大家都非常了解（如下图所示），不难看出当二叉树有n个结点的时候，有2n个指针域，但是却有n+1个指针域的指向都是空指针域，当我们寻找某一个结点的孩子结点的时候非常的方便，但是当我们想要取寻找一个结点的双亲结点，却只能通过遍历的方法去找寻，如果我们能够充分的利用这些空的指针域来表示结点的前驱和后继，毫无疑问会给我们的操作带来不小的便捷，于是产生了线索二叉树的概念。
但是如果将原来指向空的指针域指向前驱或者后继，我们会没有办法去区分是否指针域是否是线索化的指针，于是我们需要在存储结构中新增两个标志位来进去标记指针域。

```cpp
typedef struct treeNode {   //线索二叉树的存储结构 
	int data;
	treeNode *lchild,*rchild;
	int ltag, rtag;     //需要使用的标记 
}treeNode , *Tree;

之后呢我们采用递归的方式建立二叉树

void createTree(Tree &tree)   //使用递归方式创建二叉树
{
	int data;
	cin >> data;
	if(data==-1){    //输入-1代表创建结束 
	tree = NULL;
	}else{
		tree = new treeNode;
		tree->data = data;
		createTree(tree->lchild);
		createTree(tree->rchild);
	}
} 

我们可以通过便利二叉树来检查我们所建立的二叉树（最好在图上展示出来我们的逻辑结构 ） （本案例会通过最简单的逻辑结构来进行讲解）
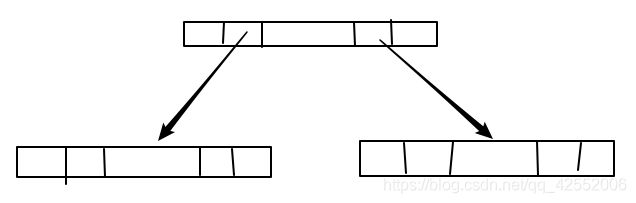现在我们建立好了一个普通的二叉树 采用递归方式建立的话 需要输入
123-1-1-1-1 来进行建立 如下图所示
现在我们要进行线索化，先把使用的方法贴出来（先序遍历二叉树进行线索化）

//没有头结点的二叉树的线索化 
treeNode *temp;  
void XXtreeTips(Tree &T){    //先序遍历线索二叉树   
	if(!T){    //如果树为空  则直接结束方法 
		return; 
	}
		if(!T->lchild){   //线索化左指针域为空的结点 
			T->lchild = temp; 
			T->ltag = 1;
		}
		if(temp!=NULL && temp->rchild == NULL){    //线索化右指针为空的结点 
			temp->rchild = T;
			temp->rtag = 1;
		}
		temp = T;
	if(T->ltag == 0){     
	XXtreeTips(T->lchild);}    //递归调用进行左子树的处理 
	if(T->rtag == 0){
	XXtreeTips(T->rchild);}    //递归调用进行右子树的处理 
}  

接下来我我们来逐步的讲解如何对这个二叉树进行线索化
1.首先我们进入方法体，指针指向根节点，且结点非空
**注意：**此时我们需要一个空指针来记录我们遍历指针访问的前一个结点

2.因为我们先序遍历的第一个结点就是根节点，但是此时我们根节点的左右指针域都是非空指针，于是我们进入第二层递归开始线索化根节点的左孩子结点。同时，将temp指向根节点。
3.根节点的左孩子结点（也就是二号结点）的左右指针域都是空，所以我们会依次执行如下两块代码。

4.执行之后，二号结点的左指针域指向了一号结点，同时标记为更改为1，但是此时temp指向的一号结点的右指针域为0（代表着右指针域指向右孩子）第二段代码并未执行，之后将temp修改为当前二号结点。
5.之后进行判断，如果当前结点的左指针域为0，则进入第三层递归，但是经过我们的线索化，二号结点的左指针域标记为此时为1，所以并未在这里进入第三层的递归，接着进行二号结点的右指针域标记位的判断，此时进入第三层的递归。
6.按照如上步骤，第三层的递归进入之后，将三号结点的左指针域修改为指向二号结点。此时，temp指向着二号结点，但是三号结点的右孩子为空指针域，所以并未修改三号结点的右指针域。之后将temp修改为三号结点。
7.注意下面第四层的递归
虽然会在第二个if之后进入第四层的递归，但是进入之后T指针会指向空结点，所以会直接返回第三层递归
8.第三层递归结束，返回第二层递归。一路返回第一层递归。此时，我们会从下面的代码再次进入递归。

9.此时我们会发现，temp和T都指向了三号节点
这些条件都不会成立。
10.我们直接进去第三层递归，但是此时第三层递归的参数传递的为空结点，再次返回第二层递归，返回第一层递归，方法结束，线索化完成。此时我们的二叉树的结构将会变成下图所示。
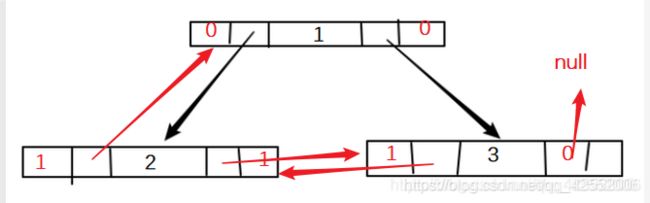线索化结束 （中序，后序 其实与上面的步骤相似 大家可以自己模拟一变，会让自己对线索化理解的非常的深刻）
*

接下来我们对上面线索化的二叉树来进行遍历

当完全理解线索化的时候，遍历也就不在话下了。老规矩，先贴代码

void printTipsTree(Tree &T){   //遍历线索化之后的二叉树 
	while(T){    //当T不为空的时候进入循环 
		while(T->ltag == 0){    //T指向的结点  有左孩子  进入循环 
			cout<<T->data<<" "<<T->ltag<<" "<<T->rtag<<endl;
			T=T->lchild;    
		}   //结束循环的时候  代表当前节点的左指针域已经被线索化   
		cout<<T->data<<" "<<T->ltag<<" "<<T->rtag<<endl;   //输出当前节点 
		T = T->rchild;  //最后一个节点的右指针为空  结束整个循环 
	} 
}

大家可以看到 这里我们并没有使用递归的方法，所以理解起来也就会轻松很多。看下图 看下图
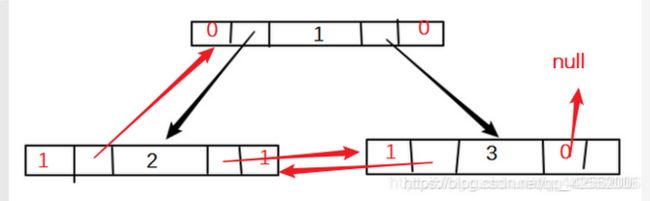我们进入外层循环，这时候T指向根节点（一号结点），此时判断一号结点是否有未经线索化的左指针域，进入内层循环，输出当前结点的数据以及标记。
接下来我们修改T指针，T指向二号结点，但是此时二号结点的左指针域已经线索化，所以直接跳出内层循环，输出数据。修改T指针，指向线索化之后的二号结点的右指针域（三号结点）
再次进去外层循环，此时T指向三号结点，且三号结点的左指针域已经线索化，所以我们直接输出数据，再次修改T指针，让T指向三号结点的右指针域，我们会发现，T指针已经指向了NULL，此时结束外层循环，遍历结束。
怎么样，是不是比线索化理解起来简单多了。（这是使用后继指针来进行线索遍历的方式）。

带有头结点

我们学习链表的时候，会发现添加一个头结点会节省很多特殊的操作，那么我们的线索二叉树是否能够 添加头结点呢 答案当然是肯定的
先上代码

//带有头结点的二叉树的线索化
treeNode *head = new treeNode;   //建立全局变量的头结点 
void   withHeadNodeTips(Tree &T){
	head->ltag = 0;    //头结点的左指针域始终会有指向
	head->rtag = 1; 
	head->rchild = head;   //初始化时，右指针域指向自身
	if(!T){   //判断树是否为空 
		T->lchild = T;   //如果树为空  那么头结点的左指针域指向自身 
	} else{
		head->lchild = T;    //否则  将 头结点的左指针域指向非空树 
		temp = head;      //当根节点没有左子树的时候  需要使用头结点 
		XXtreeTips(T);   //调用线索化二叉树的方法进行线索化
		temp->rchild = head;  //结束调用的时候  temp指向最后访问的结点 
		temp->rtag = 1;
		head->rchild = temp;//结束的时候  更改头结点的右指针域 
	}
}   

**注意：**此时我们需要定义一个全局变量的头结点。

没有涉及递归 也 非常容易理解。
初始化的时候，头结点的左指针域指向二叉树的根节点，并把右指针域指向自身，修改线索化标记。
如果树为空，那么左指针域也指向自身。
否则将头结点的左指针域指向二叉树，同时将temp指向头结点。
调用之前先序线索化的方法
从上面方法的讲解我们可以看到，temp最后的指向是最后一个节点（3号节点），此时我们修改三号节点的右指针域，指向头结点，并且修改线索化标记。同时将 头结点的右指针域修改为最后一个节点。
修改过之后，逻辑结构如下图所示。

带有头结点的遍历

废话少说 直接上代码 经过前面的理解，我相信下面的代码也难不倒大家，在这里我就不再赘述

//遍历带有头结点的线索二叉树
void withHeadPrint(Tree &T){
	treeNode *p = T->lchild;     //定义一个新的遍历结点  也可以直接使用T指针 
	while(p!=head){         //当p指针不为空的时候进入循环 
		cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;   //输出数据 
		while(p->ltag == 0){      //当p所指向的结点的左指针域标记为0时进入循环 
			p=p->lchild;     //p结点修改为p结点的左孩子 
			cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;    //输出数据 
		}
		while(p->rtag == 1 && p->rchild!=T){     //当p结点的右指针域不为根节点时  且 经过了线索化 
			p=p->rchild;     //修改p指针   指向p的右指针域 
			cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;   //输出数据 
		}
		p=p->rchild;    //当遍历到最后一个节点   p将会指向头结点   结束遍历 
	}
} 

下面是完整的代码

#include 
using namespace std;

typedef struct treeNode {   //线索二叉树的存储结构 
	int data;
	treeNode *lchild,*rchild;
	int ltag, rtag;     //需要使用的标记 
}treeNode , *Tree;
	treeNode *temp;
void createTree(Tree &tree)   //使用递归方式创建二叉树
{
	int data;
	cin >> data;
	if(data==-1){    //输入-1代表创建结束 
	tree = NULL;
	}else{
		tree = new treeNode;
		tree->data = data;
		createTree(tree->lchild);
		createTree(tree->rchild);
	}
} 
void print(Tree &T){   //遍历输出建立的二叉树 
	if(T){
		cout<<T->data<<" "<<T->ltag<<" "<<T->rtag<<endl;   
		print(T->lchild);
		print(T->rchild);
	}
}
void printTipsTree(Tree &T){   //遍历线索化之后的二叉树 
	while(T){    //当T不为空的时候进入循环 
		while(T->ltag == 0){    //T指向的结点  有左孩子  进入循环 
			cout<<T->data<<" "<<T->ltag<<" "<<T->rtag<<endl;
			T=T->lchild;    
		}   //结束循环的时候  代表当前节点的左指针域已经被线索化   
		cout<<T->data<<" "<<T->ltag<<" "<<T->rtag<<endl;   //输出当前节点 
		T = T->rchild;  //最后一个节点的右指针为空  结束整个循环 
	} 
}
//没有头结点的二叉树的线索化 
void XXtreeTips(Tree &T){    //先序遍历线索二叉树   
	if(!T){    //如果树为空  则直接结束方法 
		return; 
	}
		if(!T->lchild){   //线索化左指针域为空的结点 
			T->lchild = temp; 
			T->ltag = 1;
		}
		if(temp!=NULL && temp->rchild == NULL){    //线索化右指针为空的结点 
			temp->rchild = T;
			temp->rtag = 1;
		}
		temp = T;
	if(T->ltag == 0){     
	XXtreeTips(T->lchild);}    //递归调用进行左子树的处理 
	if(T->rtag == 0){
	XXtreeTips(T->rchild);}    //递归调用进行右子树的处理 
}  
//带有头结点的二叉树的线索化
treeNode *head = new treeNode;   //建立全局变量的头结点 
void   withHeadNodeTips(Tree &T){
	head->ltag = 0;    //头结点的左指针域始终会有指向
	head->rtag = 1; 
	head->rchild = head;   //初始化时，右指针域指向自身
	if(!T){   //判断树是否为空 
		T->lchild = T;   //如果树为空  那么头结点的左指针域指向自身 
	} else{
		head->lchild = T;    //否则  将 头结点的左指针域指向非空树 
		temp = head;      //当根节点没有左子树的时候  需要使用头结点 
		XXtreeTips(T);   //调用线索化二叉树的方法进行线索化
		temp->rchild = head;  //结束调用的时候  temp指向最后访问的结点 
		temp->rtag = 1;
		head->rchild = temp;//结束的时候  更改头结点的右指针域 
	}
}   
//遍历带有头结点的线索二叉树
void withHeadPrint(Tree &T){
	treeNode *p = T->lchild;     //定义一个新的遍历结点  也可以直接使用T指针 
	while(p!=head){         //当p指针不为空的时候进入循环 
		cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;   //输出数据 
		while(p->ltag == 0){      //当p所指向的结点的左指针域标记为0时进入循环 
			p=p->lchild;     //p结点修改为p结点的左孩子 
			cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;    //输出数据 
		}
		while(p->rtag == 1 && p->rchild!=T){     //当p结点的右指针域不为根节点时  且 经过了线索化 
			p=p->rchild;     //修改p指针   指向p的右指针域 
			cout<<p->data<<" "<<p->ltag<<" "<<p->rtag<<endl;   //输出数据 
		}
		p=p->rchild;    //当遍历到最后一个节点   p将会指向头结点   结束遍历 
	}
} 
int main ()
{
	Tree T ;
	createTree(T);	
	print(T);
	
	//由于使用的是同一颗树  测试不带有头结点的时候  请将下面测试带头结点的三行注释  
	XXtreeTips(T);
	cout<<"-------"<<endl;
	printTipsTree(T);
	
	
//	withHeadNodeTips(T);     //由于使用的是同一颗树  测试带有头结点的时候  请将上面三行注释   
//	cout<<"-------"<
//	withHeadPrint(head);


	return 0;
 } 

如果程序报错 请注意看注释！！！