材料力学:使用matlab绘制铰支梁在多个集中力、集中力偶矩作用下的挠曲线
材料力学:使用matlab绘制铰支梁在多个集中力、集中力偶矩作用下的挠曲线
-
- **一、程序输入参数介绍**
- **二、程序设计思路介绍**
-
- **1.输入变量预处理**
- **2.支座反力求解**
- **3.梁的弯矩求算**
- **4.数值积分法求解挠度**
- **5.曲线绘制及关键点标注**
- **三、程序源码**
20220709修改:后续的悬臂梁以及均布载荷的求算已经加上啦!同时我将它做成了matlab的APP,详情转到我的新博客:
【材料力学】基于Matlab APP Designer 开发的绘制静定梁剪力、弯矩与挠曲线的软件
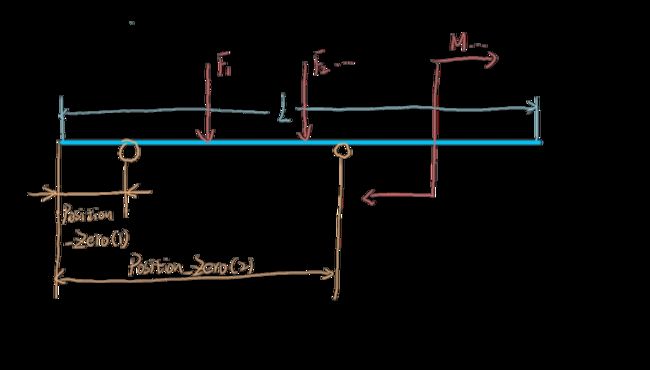
梁的弯曲变形时材料力学中十分重要的研究内容,我自行设计了matlab代码以求算通过铰支座固定的梁,在多个外加集中力或是集中力偶矩的作用下,绘制梁统一的挠曲线(悬臂梁与集中载荷功能后续开发)。如有错误,欢迎交流指正。
一、程序输入参数介绍
相应的,程序中的输入变量如下:
EI = 3 ; %定义梁的弯曲刚度
Length = 1 ; %定义梁的总长度
Position_Zero = [0.1,0.85]; %定义位移为零的点的坐标(铰支座)
Angle_Zero = [0,0] ; %定义转角为零的点的坐标(悬臂等)
Single_Force = [0.4 , 10;
0.5, -5 ;
0.7 , 8]; %定义集中力作用的位置及大小(向下为正)
Single_Torque = [0.2 , 12 ;
0.4 , -7 ;]; %定义集中集中力偶矩作用的位置及大小(向下为正)
程序可设定梁的弯曲刚度EI ,单位为 N/m,梁的长度单位为m,Position_Zero 为统一以梁的左端为坐标原点时两个铰支座的坐标(如上图中标出)。
Angle_Zero 为转角为零的点,如悬臂梁的末端等,因程序中暂未编写悬臂梁的求解,因此此项暂设为0。Single_Force为集中力的输入信息,矩阵第一列为集中力的施加点坐标,第二列为集中力的大小,集中力规定为向下为正。数组允许输入多行,每行相当于一个集中力。Single_Torque矩阵的输入方式类似,将集中力偶矩的正方向规定为顺时针。完成输入后,运行程序,会解算出当前载荷情况下梁的弯矩图与相应的挠曲线。
二、程序设计思路介绍
1.输入变量预处理
程序采用了微元化的思想,将梁的总长度划分为50000份微元(调节程序中的fineness参数来变换微元数量,当梁较长时,可以根据需要提高微元数目)。而使用者输入的外载荷的位置可能不在微元划分后的“标准坐标点”上,因此,有必要使程序有能力自主修复使用者的输出参数。为了达到这一目的,同时为了便于后续计算过程的展开,在完成输入变量后,程序将得到以下预处理信息:
num_Force = size(Single_Force,1);
num_Torque = size(Single_Torque,1); %求解集中力与集中力偶矩的个数
Solve_Mode = 0 ; % 0 为仅含铰支座结构,1为含有悬臂结构,本版本仅可求解含铰支座版本
fineness = 50000; % 梁的长度的精细度,即微元份数
division_Value = Length/fineness ; %定义梁长度分度值
其中division_Value即为微元的长度,基于这些信息,设计的坐标点“标准化”函数如下:
%%
function [axis] = axis_regularize(input,division_Value,number) %将作用点"微移动"至标准微元点
for i = 1:number
rate = input(i,1) / division_Value;
input(i,1) = round(rate) * division_Value;
end
axis = input;
end
该函数会将input矩阵的第一列标准化至标准的微元坐标上。即实现作用点的“微移动”,这样的微移动对实际的计算结果实际上没有影响。至此,进一步调用axis_regularize 函数即可完成对输入载荷的规范化:
Single_Torque = axis_regularize(Single_Torque,division_Value,num_Torque);
Single_Force = axis_regularize(Single_Force,division_Value,num_Force);
2.支座反力求解
在完成了上述的标准化之后,便可以开始求解铰支座的反力,因为铰支座的反力都是沿铅直方向,因此统一通过“对A支座取矩求单个外载荷作用下的B支座力 -> 所求的所有B支座力叠加 -> 利用
![]()
求解A支座力”的流程来实现,具体代码如下:
for i = 1:num_Force %计算集中力对铰支座B的支座力
Support_B = Support_B - (Single_Force(i,1) - ...
Position_Zero(1))*Single_Force(i,2)/(Position_Zero(2) - Position_Zero(1));
end
for i = 1:num_Torque
Support_B = Support_B - Single_Torque(i,2)/(Position_Zero(2) - Position_Zero(1)) ;
end %计算集中力偶矩对支座B的支座力
Support_A = -Support_B - sum(Single_Force(:,2)); %求解综合B支座力与外载荷的影响下A支座的支座力
至此,可以将所有支座撤去,得到纯受力图。
3.梁的弯矩求算
梁的弯矩求算则采取叠加原理的思想对包括铰支座支座力在内的所有载荷逐一求算其对梁的弯矩的影响,使用统一行向量叠加计算的方式直接完成叠加计算:
%%
%叠加原理求算弯矩
for i = 1:num_Torque
serial = Single_Torque(i,1) / division_Value ; %集中力偶矩的施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial == 0
serial = 1;
end
Torque(serial:fineness) = Torque(serial:fineness) + Single_Torque(i,2);
end
for i = 1:num_Force
serial = Single_Force(i,1) / division_Value ; %集中力的施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial == 0
serial = 1;
end
Torque(serial:fineness) = Torque(serial:fineness) - Single_Force(i,2)*(x(serial:fineness) - Single_Force(i,1));
end
serial_A = Position_Zero(1) / division_Value ; %支座A施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial_A == 0
serial_A = 1;
end
Torque(serial_A:fineness) = Torque(serial_A:fineness) - Support_A*(x(serial_A:fineness) - Position_Zero(1));
serial_B = Position_Zero(2) / division_Value ; %支座B施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial_B == 0
serial_B = 1;
end
Torque(serial_B:fineness) = Torque(serial_B:fineness) - Support_B *(x(serial_B : fineness) - Position_Zero(2));
end
上述代码执行完毕后,即可得到长度为fineness的行向量,其中的弯矩值与x行向量中的坐标值一一对应。
4.数值积分法求解挠度
因为:
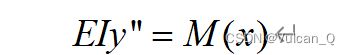
则对弯矩值做两次积分,除掉梁的弯曲刚度EI ,即可得到梁的挠度值,为了提高微元算法的准确度,我使用了当前微元面积与前后共三个微元面积和的平均值作为当前位置的积分微元值,两次积分操作如下:
%两次数值积分求挠度
for i = 2:fineness-1
Theta(i) = (Torque(i-1) + Torque(i) + Torque(i+1)) / 3 * division_Value ; %积分微元求算
end
Theta(1) = Theta(2);
Theta(fineness) = Theta(fineness - 1); %边缘直接取等
Theta = cumsum(Theta); %累加积分
Deflection = zeros(size(Theta));
for i = 2:fineness-1
Deflection(i) = (Theta(i-1) + Theta(i) + Theta(i+1)) / 3 * division_Value;
end
Deflection(1) = Deflection(2);
Deflection(fineness) = Deflection(fineness - 1);
Deflection = cumsum(Deflection);
但仅仅进行两次积分是不够的,这相当于求解了两次数值不定积分,忽视了积分过程中产生的常数项,即真正的挠度应表示为:
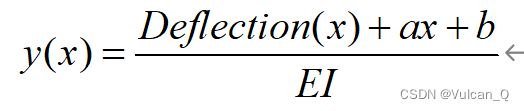
而两个待定系数a、b则通过带入铰支座处的坐标求得(铰支座的挠度为0):
Serial_Position_Zero = Position_Zero./division_Value;
if Serial_Position_Zero(1)==0
Serial_Position_Zero(1) = 1;
end
Serial_Position_Zero(2) = round( Serial_Position_Zero(2));
A =[x(Serial_Position_Zero(1)) , 1;
x(Serial_Position_Zero(2)), 1];
b = [-Deflection(Serial_Position_Zero(1));
-Deflection(Serial_Position_Zero(2))];
C = A\b;
Deflection(1:fineness) = (Deflection(1:fineness) + C(1)*x(1:fineness)+C(2))/EI;
至此,便完成了整个挠度的计算过程。
5.曲线绘制及关键点标注
这部分就是较为简单的绘图功能了,不做详细介绍,具体代码如下:
Max_Deflection = max(abs(Deflection(1:fineness)));
Max_Position = [];
for i = 1:fineness
if abs(Deflection(i)) == Max_Deflection
Max_Position = [Max_Position , i];
end
end
subplot(2,1,1)
plot (x,Torque,Color='k');
title("梁的弯矩图")
subplot(2,1,2)
plot(x,Deflection,LineStyle="--",Color='r');
hold on
plot([0,Length],[0,0],LineStyle="-.",Color='k');
title("梁的挠曲线")
if Max_Position ~= 0 %标注出挠度最大点的位置及挠度值
for i = 1 : size(Max_Position,1)
plot(x(Max_Position(i)) , Deflection(Max_Position(i)),"-*",Color="b");
text( x(Max_Position(i)) , Deflection(Max_Position(i)) , ...
['(',num2str(x(Max_Position(i))),',',num2str(Deflection(Max_Position(i))),')'])
end
end
axis equal
三、程序源码
%%
% Author: Vulcan
% Data : 2022.5.30
%% 参数定义
clear;
close all;
clc;
EI = 3 ; %定义梁的弯曲刚度
Length = 1 ; %定义梁的总长度
Position_Zero = [0.1,0.85]; %定义位移为零的点的坐标(铰支座)
Angle_Zero = [0,0] ; %定义转角为零的点的坐标(悬臂等)
Single_Force = [0.4 , 10;
0.5, -5 ;
0.7 , 8]; %定义集中力作用的位置及大小(向下为正)
Single_Torque = [0.2 , 12 ;
0.4 , -7 ;]; %定义集中集中力偶矩作用的位置及大小(向下为正)
num_Force = size(Single_Force,1);
num_Torque = size(Single_Torque,1); %求解集中力与集中力偶矩的个数
Solve_Mode = 0 ; % 0 为仅含铰支座结构,1为含有悬臂结构,本版本仅可求解含铰支座版本
fineness = 50000; % 梁的长度的精细度,即微元份数
division_Value = Length/fineness ; %定义梁长度分度值
Single_Torque = axis_regularize(Single_Torque,division_Value,num_Torque);
Single_Force = axis_regularize(Single_Force,division_Value,num_Force);
%% 求解运算
Support_B = 0;
x = linspace(0,Length,fineness); %将梁按精细度划分
Torque = zeros(size(x));
Theta = zeros(size(x));
if Solve_Mode == 0 %简支模式下求支座反力
for i = 1:num_Force %计算集中力对铰支座B的支座力
Support_B = Support_B - (Single_Force(i,1) - ...
Position_Zero(1))*Single_Force(i,2)/(Position_Zero(2) - Position_Zero(1));
end
for i = 1:num_Torque
Support_B = Support_B - Single_Torque(i,2)/(Position_Zero(2) - Position_Zero(1)) ;
end %计算集中力偶矩对支座B的支座力
Support_A = -Support_B - sum(Single_Force(:,2)); %求解综合B支座力与外载荷的影响下A支座的支座力
%%
%叠加原理求算弯矩
for i = 1:num_Torque
serial = Single_Torque(i,1) / division_Value ; %集中力偶矩的施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial == 0
serial = 1;
end
Torque(serial:fineness) = Torque(serial:fineness) + Single_Torque(i,2);
end
for i = 1:num_Force
serial = Single_Force(i,1) / division_Value ; %集中力的施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial == 0
serial = 1;
end
Torque(serial:fineness) = Torque(serial:fineness) - Single_Force(i,2)*(x(serial:fineness) - Single_Force(i,1));
end
serial_A = Position_Zero(1) / division_Value ; %支座A施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial_A == 0
serial_A = 1;
end
Torque(serial_A:fineness) = Torque(serial_A:fineness) - Support_A*(x(serial_A:fineness) - Position_Zero(1));
serial_B = Position_Zero(2) / division_Value ; %支座B施加位置坐标除以分度精度得到对应的点在数组中的序号
if serial_B == 0
serial_B = 1;
end
Torque(serial_B:fineness) = Torque(serial_B:fineness) - Support_B *(x(serial_B : fineness) - Position_Zero(2));
end
%两次数值积分求挠度
for i = 2:fineness-1
Theta(i) = (Torque(i-1) + Torque(i) + Torque(i+1)) / 3 * division_Value ; %积分微元求算
end
Theta(1) = Theta(2);
Theta(fineness) = Theta(fineness - 1); %边缘直接取等
Theta = cumsum(Theta); %累加积分
Deflection = zeros(size(Theta));
for i = 2:fineness-1
Deflection(i) = (Theta(i-1) + Theta(i) + Theta(i+1)) / 3 * division_Value;
end
Deflection(1) = Deflection(2);
Deflection(fineness) = Deflection(fineness - 1);
Deflection = cumsum(Deflection);
Serial_Position_Zero = Position_Zero./division_Value;
if Serial_Position_Zero(1)==0
Serial_Position_Zero(1) = 1;
end
Serial_Position_Zero(2) = round( Serial_Position_Zero(2));
A =[x(Serial_Position_Zero(1)) , 1;
x(Serial_Position_Zero(2)), 1];
b = [-Deflection(Serial_Position_Zero(1));
-Deflection(Serial_Position_Zero(2))];
C = A\b;
Deflection(1:fineness) = (Deflection(1:fineness) + C(1)*x(1:fineness)+C(2))/EI;
Max_Deflection = max(abs(Deflection(1:fineness)));
Max_Position = [];
for i = 1:fineness
if abs(Deflection(i)) == Max_Deflection
Max_Position = [Max_Position , i];
end
end
subplot(2,1,1)
plot (x,Torque,Color='k');
title("梁的弯矩图")
subplot(2,1,2)
plot(x,Deflection,LineStyle="--",Color='r');
hold on
plot([0,Length],[0,0],LineStyle="-.",Color='k');
title("梁的挠曲线")
if Max_Position ~= 0 %标注出挠度最大点的位置及挠度值
for i = 1 : size(Max_Position,1)
plot(x(Max_Position(i)) , Deflection(Max_Position(i)),"-*",Color="b");
text( x(Max_Position(i)) , Deflection(Max_Position(i)) , ...
['(',num2str(x(Max_Position(i))),',',num2str(Deflection(Max_Position(i))),')'])
end
end
axis equal
%%
function [axis] = axis_regularize(input,division_Value,number) %将作用点"微移动"至标准微元点
for i = 1:number
rate = input(i,1) / division_Value;
input(i,1) = round(rate) * division_Value;
end
axis = input;
end