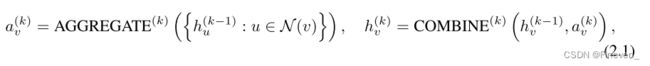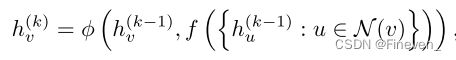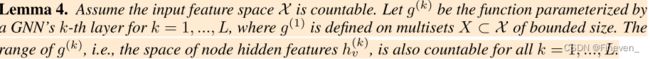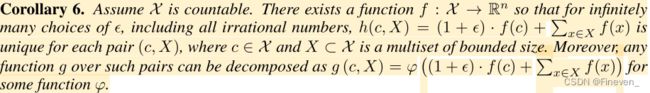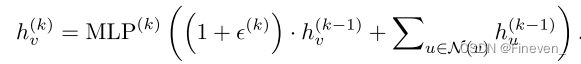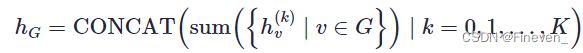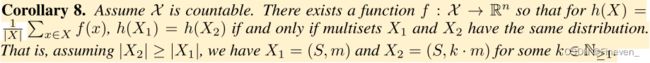论文阅读_(GIN)How Powerful are Graph Neural Networks

GIN

Introduction

GNN变体广泛遵循递归邻域聚合，其中每个节点聚合其邻居的特征向量以计算其新的特征向量。经过 k 次聚合迭代后，节点由其转换后的特征向量表示，该向量捕获节点 k 跳邻域内的结构信息。 通过池化获得整个图的表示。

GNN变体在节点分类、链接预测和图分类等许多任务中都取得了最先进的性能。 然而，GNN变体的设计主要基于经验直觉、启发式和实验性试错法。 对 GNN变体的特性和局限性的理论理解很少，对GNN变体表征能力的形式分析也很有限。

与 GNN 类似，WL 测试通过聚合其网络邻居的特征向量来迭代更新给定节点的特征向量。 WL 测试如此强大的原因在于它的单射聚合更新将不同的节点邻域映射到不同的特征向量。 如果 GNN 的聚合方案具有高度表达性并且可以模拟单射函数，则 GNN 可以具有与 WL 测试一样大的判别能力。

本文贡献如下：

1. 表明 GNN 在区分图结构方面最多与 WL 测试一样强大。
2. 建立了邻居聚合和图读出函数的条件，在这些条件下生成的 GNN 与 WL 测试一样强大。
3. 识别出流行的 GNN 变体无法区分的图结构，例如GCN和GraphSAGE，并且我们精确地表征了图结构的种类，例如基于GNN的模型可以捕捉。
4. 提出图同构网络（GIN），并表明它的判别/表示能力等于 WL test的能力。

preliminaries

GNN

GNN 通过聚合其邻居的表示来迭代更新节点的表示。k 次聚合迭代后，捕获其 k 跳网络邻域内的结构信息。GNN 的第 k 层：

hv(k)是节点 v 在第 k 次迭代/层的特征向量，N(v)是一组与 v 相邻的节点。aggregate和combine的选择特别重要

WL test

Weisfeiler-Lehman (WL) 测试是一种有效且计算效率高的测试，可以区分不同图结构。WL test迭代地聚合节点及其邻域的标签，以及将聚合标签散列成唯一的新标签。如果在某些迭代中两个图之间的节点标签不同，则该算法确定两个图是非同构的。

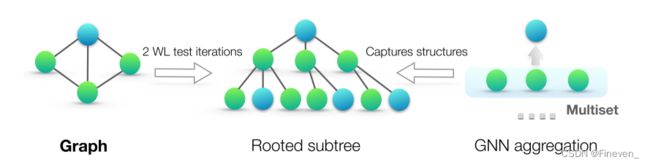
WL subtree kernel使用 WL test 的不同迭代中的节点标签计数作为图的特征向量。WL test 第k 次迭代中的节点标签表示以该节点为根的高度为 k 的子树结构，WL subtree kernel 考虑的图特征本质上是图中不同根子树的计数。

theoretical framework: overview

整篇论文中的节点输入特征来自可数空间。

定义1 (Multiset). 多重集是允许其元素有多个实例的集合的广义概念。 更正式地说，多重集是一个 2 元组 X = (S,m)，其中 S 是由其不同元素形成的 X 的基础集合，m : S → N≥1 给出了元素的多重性。

只有两个节点的子树结构相同或有相同特征，GNN才会将其映射到相同位置。进一步的，我们可以得出一个强大的GNN可以将领域相同的映射到相同的表示，意味着它的聚合方案是单射的。

building powerful graph neural network

理想情况下，GNN可以通过将他们映射到不同embedding空间来区别不同的图结构。也就是说同构图能够映射到相同的表示，非同构图映射到不同的表示。

定理2. 令 G1 和 G2 是任意两个非同构图。 如果图神经网络 A : G → Rd 将 G1 和 G2 映射到不同的嵌入，Weisfeiler-Lehman 图同构测试也决定 G1 和 G2 不是同构的。

定理2是图同质测试，说明WL test是GNN性能的上限。如果邻居聚合和图级读出函数是单射的，那么生成的 GNN 与 WL 测试一样强大。

定理3. 令 A : G → Rd 是一个 GNN。 如果有足够数量的 GNN 层，如果满足以下条件，A 会将 WL test确定为非同构的任何图 G1 和 G2 映射到不同的嵌入：

a) GNN迭代聚合和更新节点的特征：

b) GNN的readout函数是单射的

如果 GNN 中 Aggregate、Combine 和 Readout 函数是单射，GNN 可以和 WL test 一样强大。

本文中的 定理3 贯穿全文，是GIN提出的极其重要的定理依据。

定理 4. 假设输入特征空间 X 是可数的。 令 g(k) 为GNN的第k层参数化的函数，其中k = 1, …, L，其中g(1)定义在有界的多集空间x⊂X上。g(k)的范围，即节点隐藏特征的空间hv(k)，对于所有k = 1, …, L也是可数的。

GNN不仅可以区分不同的图，还可以捕捉图结构的相似性。WL test中节点特征向量的本质是one-hot编码，因此无法捕捉子树之间的相似性。相反，满足定理3 的GNN概括WL test 通过学习嵌入低维空间的子树。GNN不仅可以区分不同的结构，还可以将相同的图映射到相同的embeddig，捕捉图结构之间的依赖关系。

Graph Isomorphism Network(GIN)

在为最强大的GNN开发了条件之后，开发了一个简单的架构，即图同构网络(GIN)，它满足定理3 中的条件。该模型推广了WL test，因此在GNN变体中体现了最大的区分能力。

为邻居聚合建模单射多集函数，Lemma 5和Corollary 6阐述sum aggregators是单射的。

定理5. 假设 X 是可数的。 存在一个函数 f : X → Rn 使h(x)对于每个有界大小的多重集x⊂X都是唯一的。 此外，对于某个函数φ，任何多重集函数g都可以分解为g(x)。

我们可以设想聚合方案可以表示一个节点及其邻居的多集上的通用函数，从而满足定理3 中的单射性条件(a)。

Lemma5的证明：考虑一个有 N 个元素的multiset，对其进行任意划分，最多可以划分成N个子集，所以很自然的可以使用N个正整数对其打上唯一标记，因此证明f可以是唯一的单射函数。

推论6. 假设 X 是可数的。 存在一个函数 f : X → Rn，因此对于无限多的ϵ，括所有无理数，h(c,X)是 每对 (c,X) 都是唯一的。 此外，这些对上的任何函数 g 都可以分解为 g (c,X) 。

推论证明了h(c,X)是单射函数。我们可以用MLP去模拟推论 f 和 φ ，因为MLP是万能近似函数，可以模拟单射性质，所以MLP(h(c,X))也是单射的。

在第一次迭代中，如果输入特征是一个 one-hot，那么我们不需要在求加前使用 MLP，因为它们的 SUM 是单射的。

GIN更新节点表示：

graph-level readout of GIN

GIN的图级“读出”函数，给定单个节点的嵌入，生成整个图的嵌入。对应于子树结构的节点表示随着迭代次数的增加而变得更加精细和全局。 足够数量的迭代是获得良好判别能力的关键。 然而，早期迭代的特征有时可能会更好地概括。

Readout模块使用concat+sum，对每次迭代得到的所有节点特征求和得到图的特征，然后拼接起来。

如果 GIN 代替了方程式中的 READOUT，对来自相同迭代的所有节点特征求和

less powerful ut still interesting GNNS

不满足定理3 中条件的GNN变体，包括GCN和GraphSAGE。对两个方面进行消融研究：(1)1 层感知器而不是MLP。(2) 均值或最大池而不是总和。

1-layer perceptronns are not sufficient

许多GNN 任然采用 1 层的perceptrons，1 个线性映射和 1 个非线性激活函数，例如ReLU。定理证明1 层感知器对于某些 multiset 可能存在无法区别的问题。

一层感知器可以表现得很像线性映射，因此GNN层退化为对邻域特征的简单求和。定理 7 的证明建立在线性映射中缺乏偏差项这一事实之上。有了偏差项和足够大的输出维数，一层感知器可能能够区分不同的多集。尽管如此，与使用MLP的模型不同，一层感知器（即使有偏差项）并不是多集函数的通用逼近器。因此，即使具有1层感知器的GNN可以在一定程度上将不同的图嵌入到不同的位置，这种嵌入可能不能充分捕获结构相似性，而且简单的分类器，如线性分类器，难以拟合。具有 1 层感知器的GNN应用于图分类时，有时严重不适合训练数据，并且在测试准确性方面往往比具有MLP的GNN表现更差。

structures that confuse mean and max-pooling

将求和换成求均值或最大池化，它们不是单射的，无法区分结构对。

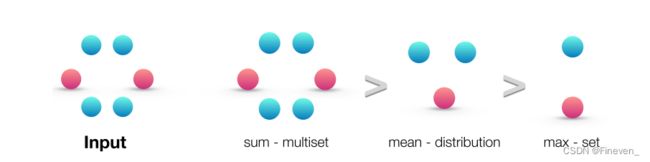
对sum、mean、max的聚合能力进行排序。

• sum:学习全部的标签和数量，可以精确的学习结构。
• mean:学习标签的比例，偏向学习分布信息。
• max:学习最大标签，偏向学习有代表性的元素。

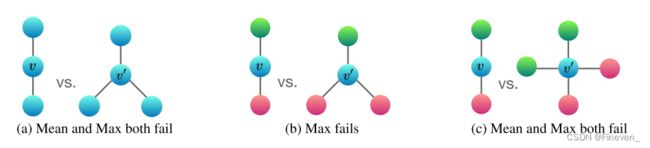
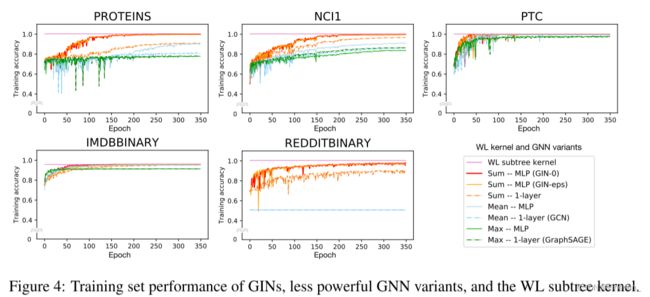
上图可以说明均值和最大值难以区分具有重复特征的节点的图。

(a) 中mean和max均为ha，无法区分；sum为2 ha和3 ha，可以区分。

(b) 中sum(hr + hg),sum(2hr + hg)，可以区分；mean中hg:hr分别为1:1, 1:2，可以区分；max中hg:hr均为1:1，无法区分。

© 中sum(hr + hg),sum(2hr + 2hg)，可以区分；mean中hg:hr均为1:1，无法区分；max中hg:hr均为1:1，无法区分。

mean leans distributions

均值聚合器可以区分的多重集类别，请考虑示例 X1 = (S,m) 和 X2 = (S, k · m)，其中 X1 和 X2 具有相同的不同元素集，但 X2 包含 k X1 的每个元素的副本。 任何平均聚合器都将 X1 和 X2 映射到相同的嵌入，因为它只是对单个元素特征取平均值。 因此，平均值捕获了多重集中元素的分布（比例），但不是精确的多重集中。

等比例的多重集，mean是无法区分的，因为mean更关注元素的比例。如果对于任务而言，图中的统计和分布信息比确切的结构更重要，则平均聚合器可能会表现良好。当节点特征多样且很少重复时，均值聚合器与总和聚合器一样强大。

max-pooling leans sets with distinct elements

最大池化将具有相同特征的多个节点仅视为一个节点，既不捕获确切的结构也不捕获分布。但是，它可能适用于重要的是识别代表性元素或“骨架”而不是区分确切的结构或分布的任务。经验表明，最大池聚合器学习识别 3D 点云的骨架，并且对噪声和异常值具有鲁棒性。

推论 9. 假设 X 是可数的。 那么存在一个函数 f : X → R∞ 使得h(X1) = h(X2)当且仅当X1和X2具有相同的基础集合。

experiments

评估和比较 GIN 和不太强大的 GNN 变体的训练和测试性能。

Datasets.使用 9 个图分类基准：4 个生物信息学数据集(MUTAG、PTC、NCI1、PROTEINS)和 5 个社交网络数据集(COLLAB、IMDB-BINARY、IMDB-MULTI、REDDITBINARY 和 REDDIT-MULTI5K)。目的不是让模型依赖输入节点特征，而是从网络结构中学习。 因此，在生物信息图中，节点具有分类输入特征，但在社交网络中没有特征。 对于社交网络，我们按如下方式创建节点特征：对于REDDIT数据集，我们将所有节点特征向量设置为相同（因此，这里的特征是无信息的）；对于其他社交图，我们使用节点度数的 one-hot 编码。

**Models and configurations.**在GIN框架下考虑两个变体：(1) 在GIN的节点更新方程中通过梯度下降学习ϵ，我们称之为GIN-ϵ。(2) 一个更简单的GIN，将ϵ固定为0，称之为GIN-0。GIN-0显示出强大的性能，不仅能够拟合训练数据，还表现出良好的泛化性，在测试准确度方面略微优于GIN-ϵ。

**Baseline.**我们将上述 GNN 与WL子树内核进行比较。

results

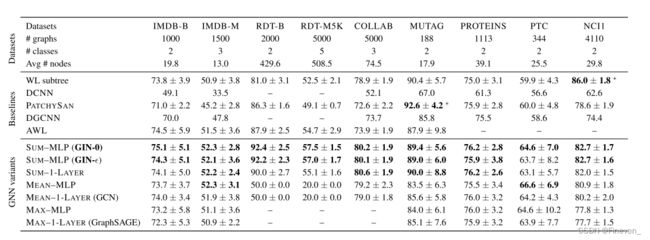
**Training set performance.**通过比较 GNN 的训练精度来验证我们对 GNN 表示能力的理论分析，具有更高表征能力的模型应该具有更高的训练集准确度。GIN-0和GIN-ϵ都能够几乎完美的拟合所有训练集，实验中，与在 GIN-0 相比，在 GIN-ϵ 中显式学习在拟合训练数据方面没有任何收益。

相比之下，使用均值/最大池或1层感知器的 GNN 变体在许多数据集上严重欠拟合。具有MLP的GNN 变体往往比具有1层感知器的GNN变体具有更高的训练准确度，而具有总和聚合器的GNN往往比那些更适合训练集使用均值和最大池化聚合器。在我们的数据集上，GNN的训练精度永远不会超过 WL 子树内核的精度。 这是意料之中的，因为 GNN 通常比 WL 测试具有更低的判别能力。

在IMDBBINARY上，没有一个模型可以完美地拟合训练集，而GNN最多可以达到与 WL 内核相同的训练精度。 这种模式与我们的结果一致，即 WL 测试为基于聚合的 GNN 的表示能力提供了上限。 然而，WL 内核无法学习如何组合节点特征，这对于给定的预测任务可能会提供相当多的信息。

**Test set performance.**接下来，我们比较测试精度。虽然我们的理论结果并没有直接说明 GNN 的泛化能力，但可以合理地期望具有强大表达能力的 GNN 能够准确地捕获感兴趣的图结构，从而很好地泛化。 表中比较了 GIN（Sum-MLP）、其他 GNN 变体以及最先进的基线的测试准确度。 GIN-0，在所有 9 个数据集上都优于不太强大的 GNN 变体。 GIN 在社交网络数据集上表现更好，其中包含相对大量的训练图。 对于 Reddit 数据集，所有节点共享与节点特征相同的标量。 在这里，GIN变体和 sum-aggregation GNNs 准确地捕获了图结构并显着优于其他模型。 然而，均值聚合 GNN 无法捕获未标记图的任何结构，并且性能不如随机猜测。 即使将节点度数作为输入特征提供，基于均值的 GNN 的性能也比基于和的 GNN 差得多（具有均值 MLP 聚合的 GNN 在 REDDIT-BINARY 上的准确度为 71.2±4.6%，在 REDDIT-BINARY 上为 41.3±2.1%。 多 5K）。 比较 GIN（GIN-0 和 GIN-），我们观察到 GIN-0 略微但始终优于 GIN-ϵ。 由于两个模型都同样适合训练数据，因此与 GIN-ϵ 相比，GIN-0 的简单性可以解释其更好的泛化性。

可以得出：

• GIN-0因为更简单，所以有更好的泛化性。

• GIN比WL test效果好，因为GIN进一步考虑了结构相似性，即WL test最终是one-hot输出，而GIN是将WL test映射到低维的embedding。

• max 在无节点特征的图（用度来表示特征）基本无效。

conclusion

本文主要基于对graph分类，证明了 sum 比 mean 、max 效果好，但是不能说明在node 分类上也是这样的效果，另外可能优先场景会更关注邻域特征分布， 或者代表性， 故需要都加入进来实验。