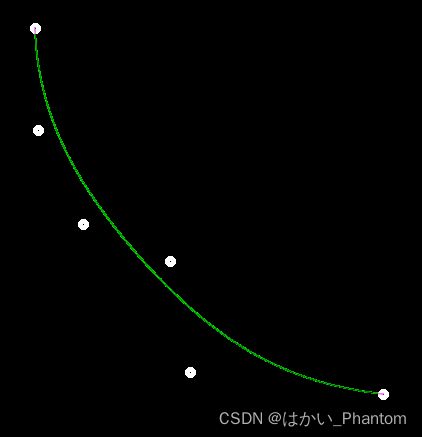
Games101第四次作业
1.任务要求
Bézier曲线是一种用于计算机图形学的参数曲线。在本次作业中,你需要实现deCasteljau算法来绘制由4个控制点表示的Bézier曲线(当你正确实现该算法时,你可以支持绘制由更多点来控制的Bézier曲线)。你需要修改的函数在提供的main.cpp文件中。
•bezier:该函数实现绘制Bézier曲线的功能。它使用一个控制点序列和一个OpenCV::Mat对象作为输入,没有返回值。它会使t在0到1的范围内进行迭代,并在每次迭代中使t增加一个微小值。对于每个需要计算的t,将调用另一个函数recursive_bezier,然后该函数将返回在Bézier曲线上t处的点。最后,将返回的点绘制在OpenCV::Mat对象上。
•recursive_bezier:该函数使用一个控制点序列和一个浮点数t作为输入,实现deCasteljau算法来返回Bézier曲线上对应点的坐标。
2.算法
DeCasteljau算法说明如下:
1.考虑一个p0,p1,…pn为控制点序列的Bézier曲线。首先,将相邻的点连接起来以形成线段。
2.用t:(1−t)的比例细分每个线段,并找到该分割点。
3.得到的分割点作为新的控制点序列,新序列的长度会减少一。
4.如果序列只包含一个点,则返回该点并终止。否则,使用新的控制点序列并转到步骤1。使用[0,1]中的多个不同的t来执行上述算法,就能得到相应的Bézier曲线。
3.代码
对应的步骤分析都写在注释里
bezier函数
//该函数实现绘制Bézier曲线的功能。它使用一个控制点序列和一个OpenCV::Mat对象作为输入,没有返回值。
//它会使t在0到1的范围内进行迭代,并在每次迭代中使t增加一个微小值。
//对于每个需要计算的t,将调用另一个函数recursive_bezier,然后该函数将返回在Bézier曲线上t处的点。
//最后,将返回的点绘制在OpenCV::Mat对象上
void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
float t0 = 0.0001;//定义一个微小值
for (double t = 0; t < 1; t += t0)
{
auto point= recursive_bezier(control_points, t);//接收每一个t时刻所对应绘制的贝塞尔曲线的点
window.at <cv::Vec3b>(point.y, point.x)[1] = 255;//Mat.at<存储类型名称>(行,列)[通道]
}
}
注意这行代码:
window.at <cv::Vec3b>(point.y, point.x)[1] = 255;//Mat.at<存储类型名称>(行,列)[通道]
通道:0-R,1-G,2-B,要求设为绿色,所以通道为1
recursive_bezier函数
//该函数使用一个控制点序列和一个浮点数t作为输入,实现deCasteljau算法来返回Bézier曲线上对应点的坐标
//该函数只是计算在某一时刻t下的对应贝塞尔曲线的点
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float &t)
{
// TODO: Implement de Casteljau's algorithm
if (control_points.size() == 2)
{
return Proportional_interpolation(control_points[0],control_points[1],t);
}
std::vector<cv::Point2f> control_points_last;//定义一个新的容器,用来接受一次比例插值之后的点
for (int i = 0; i < control_points.size() - 1; i++)
{
control_points_last.push_back(Proportional_interpolation(control_points[i], control_points[i + 1], t));
}
return recursive_bezier(control_points_last, t);
}
用一下递归就可以
Proportional_interpolation函数
//对传入的两个点坐标按比例插值,找出对应点
cv::Point2f Proportional_interpolation(const cv::Point2f &control_points_1, const cv::Point2f &control_points_2, float &t)
{
return control_points_1 * (1 - t) + control_points_2 * t;
}
naive_bezier函数
这是纯数学方法的代码,可供参考
void naive_bezier(const std::vector<cv::Point2f>& points, cv::Mat& window)
{
auto& p_0 = points[0];
auto& p_1 = points[1];
auto& p_2 = points[2];
auto& p_3 = points[3];
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 +
3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3;
window.at<cv::Vec3b>(point.y, point.x)[2] = 255;
}
}
4.结果展示



结果:通过在屏幕上随机用鼠标标注四个点,程序可以更具这四个点取约束、定义出一条贝塞尔曲线。
5.一些修改
1.修改为6个定义点
2.反走样
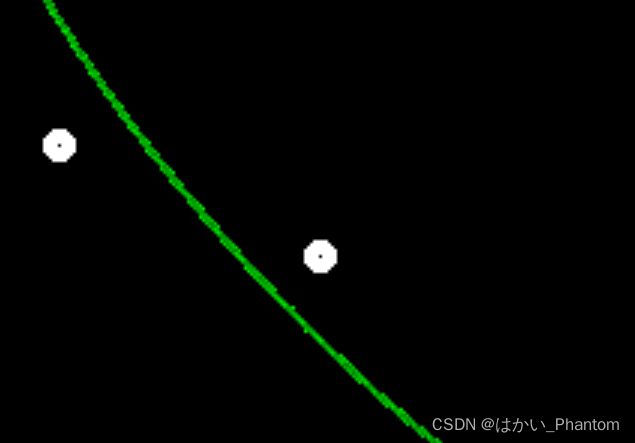
思考:因为用点来描述曲线,会因为点之间的距离或一些错位导致走样问题,可以通过对点周围像素进行适当的颜色着色,使曲线看起来更为平滑。(以下为最初的点连成的曲线,有很明显的走样,放大之后可以明显看到点与点之间的错位)
反走样做法一
思路:
程序画线主要是对点所在的像素进行着色,所以细看的话,点不是很连续,所以进行反走样的操作可以使细线更为平滑。
反走样的具体实现:
对于每个点,可以对此点到相邻像素中心(找与点最靠近的四个像素即可,一般有一个像素是包含着点)的距离,按距离的比例和着色像素颜色RGB值进行插值,对相邻的像素进行适当颜色的着色。
如下,找到点所在的四个最靠近的像素,则像素点一定会在下图黄色的方框内,所以所取点离像素点最大值为根号2,可以按比例对相邻三个像素进行颜色比例插值。
查找顺序:先找出离点最近的像素位置,再直接按坐标的相加减找出另外三个像素的坐标。(具体实现看代码过程和注释)

void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
float t0 = 0.001;//定义一个微小值
for (float t = 0.0; t <= 1.0; t += t0)
{
auto point= recursive_bezier(control_points, t);//接收每一个t时刻所对应绘制的贝塞尔曲线的点
//找出point点的周围四个像素
//先找到point点最近的像素位置,可以是包含着point点的像素,也可以是没有包含的
cv::Point2f p0(point.x - std::floor(point.x) < 0.5 ? std::floor(point.x) : std::ceil(point.x),
point.y - std::floor(point.y) < 0.5 ? std::floor(point.y) : std::ceil(point.y));
cv::Point2f p1(p0.x - 1, p0.y);//左上角的像素坐标位置,这里和下面都是用点来代表像素坐标
cv::Point2f p2(p0.x-1,p0.y-1);//左下角的像素坐标位置
cv::Point2f p3(p0.x, p0.y - 1);//右下角的像素坐标位置
std::vector<cv::Point2f> point_coordinate{ p0,p1,p2,p3 };
float max_distance = sqrt(2.0);//定义像素之间最大距离
float point_distance = 0.0f;//定义点和像素中心距离的变量
window.at <cv::Vec3b>(point.y, point.x)[1] = 255;//Mat.at<存储类型名称>(行,列)[通道]
//对四个像素进行颜色提取
for (int i = 0; i < 4; i++)
{
cv::Point2f center_coodinate(point_coordinate[i].x+0.5,point_coordinate[i].y+0.5);//定义像素中心坐标
point_distance = sqrt(pow(point.x-center_coodinate.x,2)+ pow(point.y - center_coodinate.y, 2));//求出点与当前像素中心坐标的距离
//按照point点离各像素中心点的距离/像素中心点最大距离,得出每个像素的颜色插值并着色
window.at <cv::Vec3b>(point_coordinate[i].y, point_coordinate[i].x)[1] = 255.0 * point_distance / max_distance;
}
}
}
反思:相邻像素的颜色是插值了,整体相比也更连续些,但好像并没有很好解决反走样的问题。。。(放大之后锯齿还是很明显,而且个人觉得有很严重的涂抹感),而且线也明显变粗了。。。想了一下,还是插值的颜色及做法出现问题,于是做出了下面的修改。
反走样做法二
思路:
首先上一个做法有错误的地方,就是如果只是按简单的比例(点和像素中心距离/总距离),越远的点,着色其实是越重的,所以会产生线比较粗,而且还是有走样现象。
这一次的思路是将着色比例改成:(最大像素点距离-点和当前处理的像素距离)/(A1+A2+A3+A4),
ps:最大像素点距离-点和当前处理的像素距离=Ai(i=1,2,3,4)
这样子的话,越远的点,对应比例越小,越近的点,对应比例越大。
还有,像素的颜色要在处理像素颜色通道基础上加上比例颜色,才可以和背景颜色分开。
void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
float t0 = 0.001;//定义一个微小值
for (float t = 0.0; t <= 1.0; t += t0)
{
auto point= recursive_bezier(control_points, t);//接收每一个t时刻所对应绘制的贝塞尔曲线的点
//找出point点的周围四个像素
//先找到point点最近的像素位置,可以是包含着point点的像素,也可以是没有包含的
cv::Point2f p0(point.x - std::floor(point.x) < 0.5 ? std::floor(point.x) : std::ceil(point.x),
point.y - std::floor(point.y) < 0.5 ? std::floor(point.y) : std::ceil(point.y));
cv::Point2f p1(p0.x - 1, p0.y);//左上角的像素坐标位置,这里和下面都是用点来代表像素坐标
cv::Point2f p2(p0.x-1,p0.y-1);//左下角的像素坐标位置
cv::Point2f p3(p0.x, p0.y - 1);//右下角的像素坐标位置
std::vector<cv::Point2f> point_coordinate{ p0,p1,p2,p3 };
float max_distance = sqrt(2.0);//定义像素之间最大距离
float point_distance = 0.0f;//定义点和像素中心距离的变量
float sum_distance = 0.0f;//用来记录点距离四个像素中心的总的长度
std::vector<float> distance_list{};//用来储存四个距离
for (int i = 0; i < 4; i++)
{
cv::Point2f center_coodinate(point_coordinate[i].x+0.5,point_coordinate[i].y+0.5);//定义像素中心坐标
point_distance =max_distance - sqrt(pow(point.x-center_coodinate.x,2)+ pow(point.y - center_coodinate.y, 2));//求出:像素中心最远距离-点与当前像素中心坐标的距离
//为什么这样做:因为越远的点,插值颜色越小,所以考虑线性插值按比例就这样做
distance_list.push_back(point_distance);//记录
sum_distance += point_distance;//四个循环算出总的距离长度
}
for (int i = 0; i < 4; i++)
{
float k = distance_list[i] / sum_distance;//求出距离占比系数k,离的远相对应的占比应该小一点,作为每个像素颜色的比例
window.at <cv::Vec3b>(point_coordinate[i].y, point_coordinate[i].x)[1] = std::min(255.f, window.at <cv::Vec3b>(point_coordinate[i].y, point_coordinate[i].x)[1] + 255.f * k);
//这里是对每个像素自身进行操作,自身一开始的通道颜色就是 window.at (point_coordinate[i].y, point_coordinate[i].x)[1],
//在此基础上要加上比例颜色,为了不超过255.f,要进行最小值比较
}
}
}
结果:


可以看出效果非常好,放大之后也可以看出直线很平滑,所以反走样的处理是成功的。
6.一些可参考学习的文章
1.004-Mat对象详解:
https://mbd.baidu.com/ug_share/mbox/4a83aa9e65/share?product=smartapp&tk=d4a14cfab5e6f9d436e55c8ebede9c90&share_url=https%3A%2F%2Fyebd1h.smartapps.cn%2Fpages%2Fblog%2Findex%3FblogId%3D114162214%26_swebfr%3D1%26_swebFromHost%3Dbaiduboxapp&domain=mbd.baidu.com
2.【Opencv】CV_8UC3的解析:
http://t.csdn.cn/QykfF
3.Opencv学习cvtColor函数:
https://mbd.baidu.com/ug_share/mbox/4a83aa9e65/share?product=smartapp&tk=1ba0200aff628380f2d467d7e54ad73a&share_url=https%3A%2F%2Fyebd1h.smartapps.cn%2Fpages%2Fblog%2Findex%3FblogId%3D113941015%26_swebfr%3D1%26_swebFromHost%3Dbaiduboxapp&domain=mbd.baidu.com
4.深度学习中为什么普遍使用BGR而不用RGB:
https://mbd.baidu.com/ug_share/mbox/4a83aa9e65/share?product=smartapp&tk=283013e2ba37426a636718e266019f4f&share_url=https%3A%2F%2Fyebd1h.smartapps.cn%2Fpages%2Fblog%2Findex%3FblogId%3D88211219%26_swebfr%3D1%26_swebFromHost%3Dbaiduboxapp&domain=mbd.baidu.com
5.鼠标操作setMouseCallback:
https://mbd.baidu.com/ug_share/mbox/4a83aa9e65/share?product=smartapp&tk=007080f64dcf4d02b14228ddcfdd02a7&share_url=https%3A%2F%2Fyebd1h.smartapps.cn%2Fpages%2Fblog%2Findex%3FblogId%3D105925838%26_swebfr%3D1%26_swebFromHost%3Dbaiduboxapp&domain=mbd.baidu.com
6.反走样相关算法的参考:
https://zhuanlan.zhihu.com/p/464122963?utm_id=0、
7.Opencv函数copyTo()与clone():
https://www.zhihu.com/tardis/sogou/art/400725262