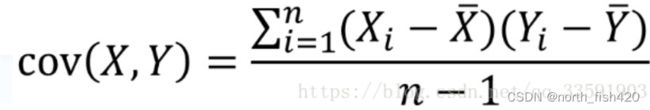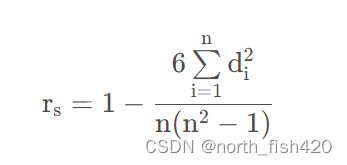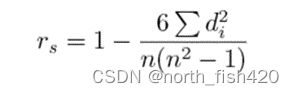EDA数据相关性分析--度量数据之间的关系
0引入
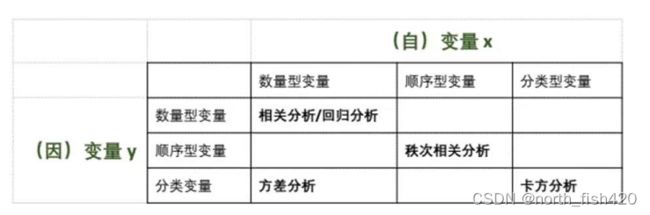
分析方法选择
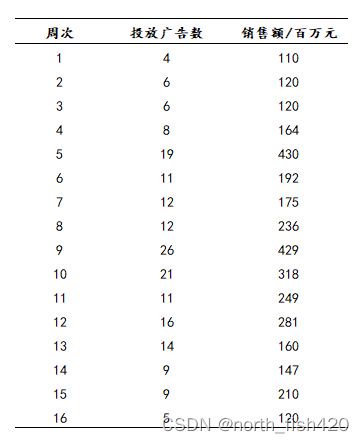
(1)广告投放对销售额的影响
存在关系吗? 关系强度与形式?总体中具备这样的关系吗?是因果关系吗?
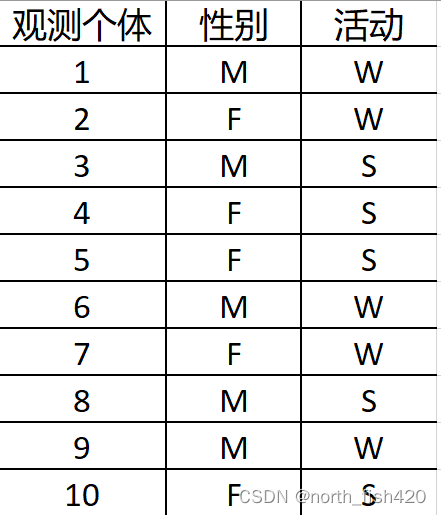
(2)营销响应中的性别差异
是否存在偏好?
(3)分析方法选择
1数量变量之间的相关性
(1)广告投放对销售额的影响
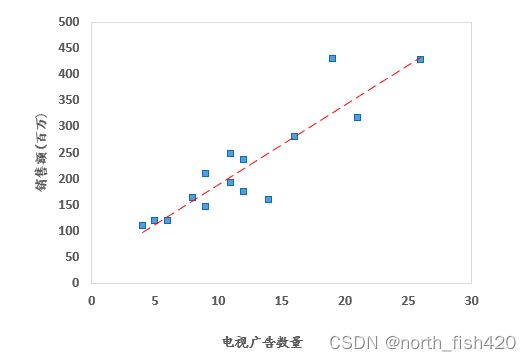
1.1散点图
1.2协方差
协方差用来衡量两个变量的总体误差,如果两个变量的变化趋势一致,协方差就是正值,说明两个变量正相关。如果两个变量的变化趋势相反,协方差就是负值,说明两个变量负相关。如果两个变量相互独立,那么协方差就是0,说明两个变量不相关。以下是协方差的计算公式:
协方差的问题是:值的大小与x和y的度量单位有关
1.3相关系数
衡量两个变量之间的强度
样本之间的相关系数用r,总体间相关系数用ρ。等于协方差除以两个变量各自的标准差。
#绘制散点图
sns.scatterplot(x='Monetary',y='Frequency',data=df)
#由散点图可以看得出来是具有相关关系的,继续计算其相关系数
#用pearson系数进行计算,可见其系数为0.95,具有较强的关系
df.corr()
#求协方差
np.cov(df['Monetary'],df['Frequency'])
#求皮尔逊系数
scipy.stats.pearsonr(df['Monetary'],df['Frequency'])
#statsmodels.formula.api.ols有关统计分析的包
from statsmodels.formula.api import ols
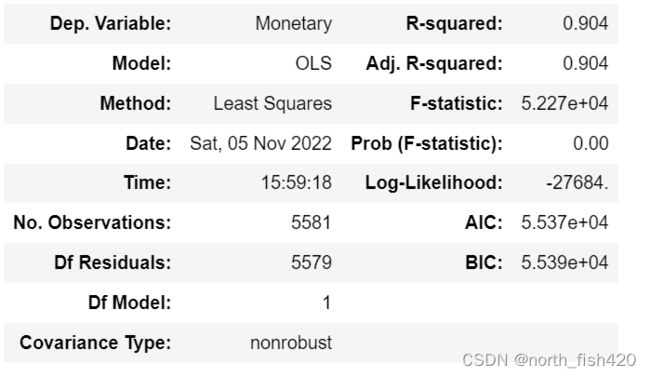
lm=ols('Monetary~Frequency',data=df).fit()
lm.summary()statsmodels.formula.api模块中ols参数的解释
(24条消息) statsmodels.formula.api模块中ols参数的解释_DeeGLMath的博客-CSDN博客_statsmodels.formula
2两个分类变量间的相关关系
(2)营销响应中的性别差异
2.1卡方分析
卡方检验是一种用途很广的假设检验方法,属于非参数检验的范畴。
主要是比较两个或两个以上样本率以及两个分类变量的关联性分析。
根本思想是在于比较理论频次与实际频次的吻合程度或拟合优度问题。
(以上简介来自网络相关文档)
卡方检验的思想为真实与理想的吻合程度。
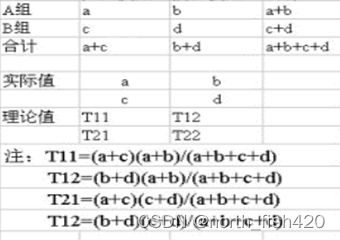
列联表:两个类别变量(定性变量)交叉分类的频数表
相关强度:
假设检验——这一篇文章就够了 - 知乎 (zhihu.com)
通过研究者的目的来判断采用哪种假设检验,若只判断是否相关采用双侧检验,判断是否正相关采用右侧检验,检验是否负相关采用左侧检验
2.2卡方检验流程
1.建立假设检验,原假设一般都是变量之间相互独立。
2.计算期望频次。
零假设H0: 性别和活动偏好之间不存在相关关系
3.代入卡方统计公式计算卡方值。
4.计算自由度。
而自由度的计算方法,可以简单抽象成(行数-1)(列数-1),所以四格表的自由度为1。
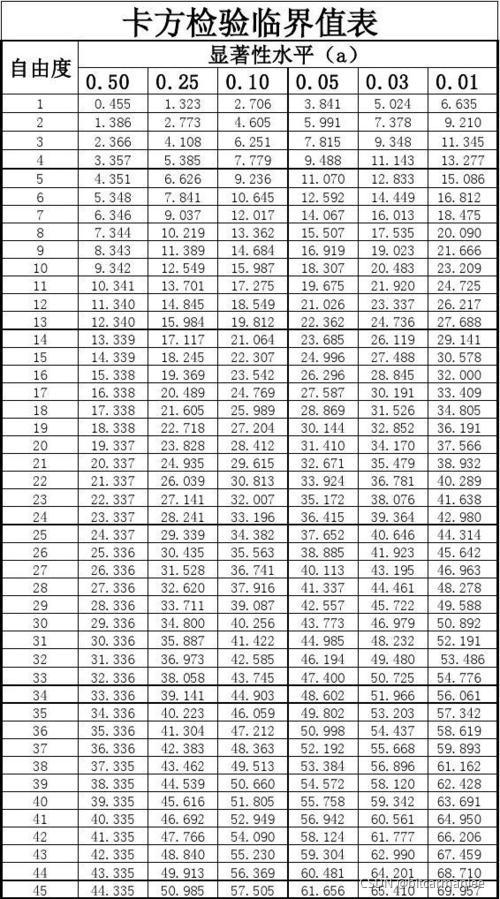
5.查表,比较卡方值或者P值或者α \alphaα值。
通过上表可以看出来,自由度为1,显著性水平为0.05,当卡方值<3.84的时候,可以接受原假设,即变量之间没有相关性。卡方值越小,不相关的概率越大。现在卡方值远大于3.84,说明两者不相关的概率很小,即营销和性别有关。
##示例2 两个分类变量的相关分析
#分析gender和member_card的相关关系
#绘制频数分布图
sns.countplot(y='member_card',hue='gender',data=df)
#输出列联表--交叉分析
pd.crosstab(df['gender'],df['member_card'])
#输出列联表--交叉分析,带行列分析,且用响度频数
pd.crosstab(df['gender'],df['member_card'],normalize=True,margins=True)
#可视化列联表发现有一定相关性,进一步进行卡方检验其显著性
table=pd.crosstab(df['gender'],df['member_card'])
table
#在python中实现卡方检验有两种方法,一种是利用scipy,另一种是sklearn
from scipy.stats import chisquare
from scipy.stats import chi2_contingency
chi2,pval,dof,expected=chi2_contingency(table)
print('理论数联表如下\n',expected)
print('p值\n',pval)
print('Null Hypothesis:零假设是性别与卡的类别是独立的,没有相关性,alpha-0.05')
if pval<0.05:
print('reject the Null Hypothesis.拒绝零假设')
else:
print('Accept the Null Hypothesis.接受零假设')3两个顺序变量之间的相关性
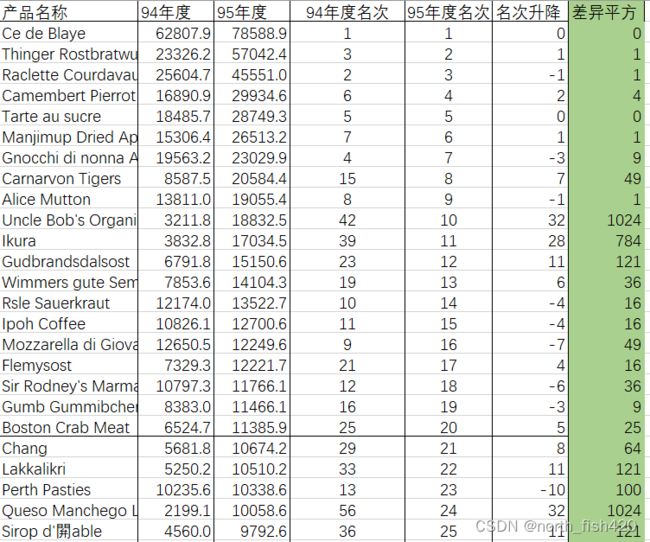
根据如下的数据,你认为随着时间的推移,产品排名会有什么样的变化,好的是否一直好?
3.1斯皮尔曼spearman相关系数
斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数
(一个数的等级就是将它所在的一列按照从小到大排列后,这个数所在的位置,可以证明,r位于-1到1之间)
注:斯皮尔曼相关系数>0为正相关;斯皮尔曼相关系数<0为负相关。越接近1和-1相关性越强。斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。
斯皮尔曼相关系数还有另一种定义方式:斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。如果数据中没有重复值,计算和上一种定义方式相同。如果有重复值,可能会有一定的偏差。
3.2spearman假设检验
正态分布小样本 t分布
对于小样本来说,如果总体分布为(近似)正态分布,则样本均值也符合(近似)正态分布,但是小样本的的方差不是总体方差σ的优良估计,这时需要用到t分布来刻画总体的方差。
定义统计量t:
如果我们从正态分布中抽取样本,则t统计量就与z统计量极其相似的抽样分布:钟型、对称、均值为0。两个分布的主要区别是t统计量比z统计量具有更大的变动性,因为t统计量包含随机变量x_bar和s,而z统计量仅包含x_bar。
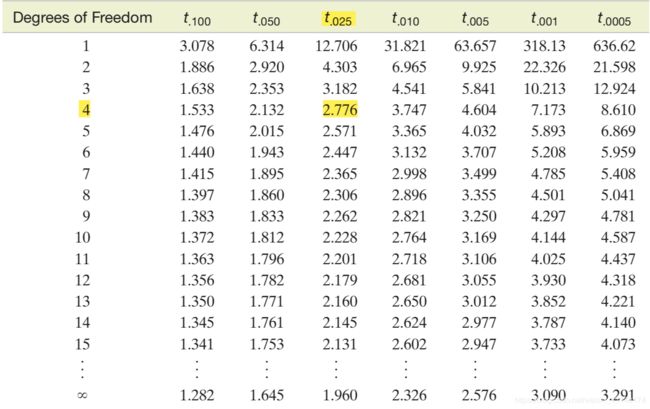
t统计量的抽样分布的总变异性取决于样本量n,假设样本数为n,则称df=n-1为t分布的自由度。一般来说t分布比正态分布更宽、更扁平,当n趋紧于总体时,t分布就时总体正态分布,s-->σ
t分布表如下:
4分类变量与数量变量间的相关性
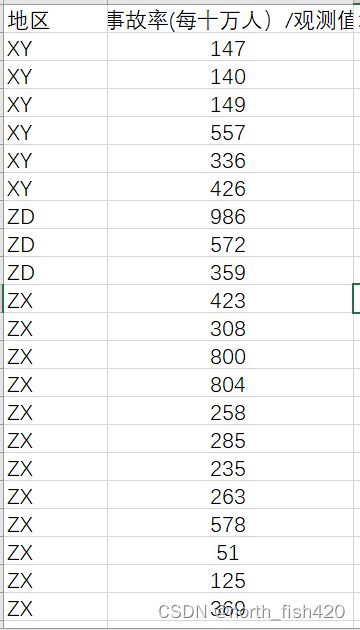
(4)事故率与地区间的关系
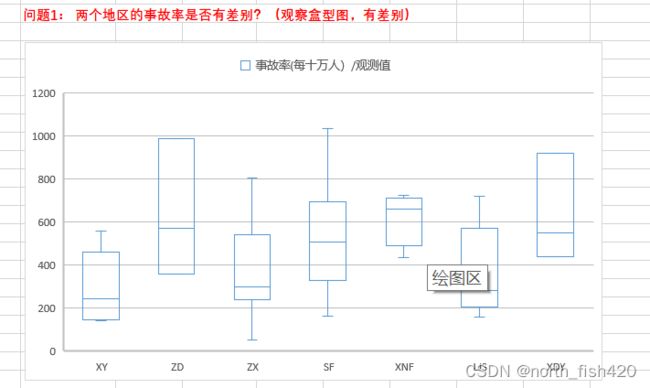
4.1描述数据分布--箱线图
箱形图(Box-plot)又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。
一组数据按照从小到大顺序排列后,把该组数据四等分的数,称为四分位数。第一四分位数 (Q1)、第二四分位数 (Q2,也叫“中位数”)和第三四分位数 (Q3)分别等于该样本中所有数值由小到大排列后第25%、第50%和第75%的数字。第三四分位数与第一四分位数的差距又称四分位距(interquartile range, IQR)。
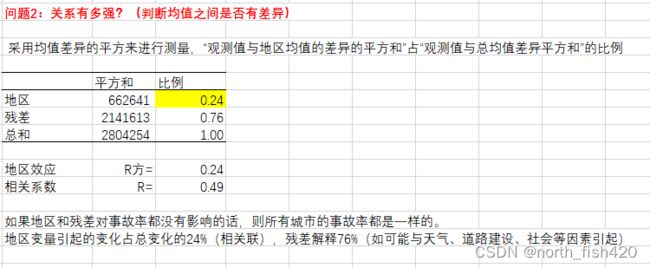
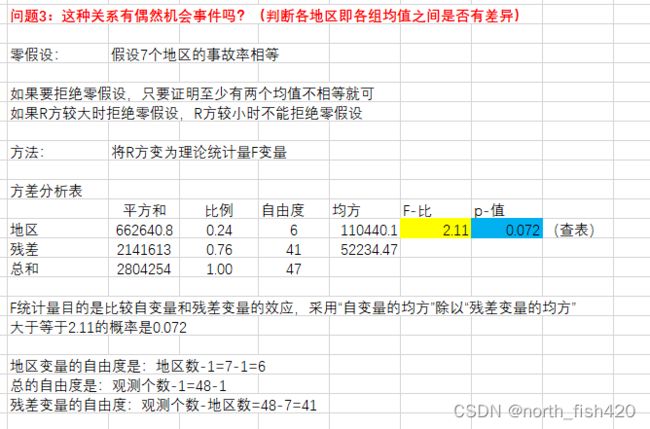
4.2方差分析
知识点链接(24条消息) 方差分析知识点汇总_哆啦A梦_i的博客-CSDN博客_方差分析
#示例3 分类型变量与数值型变量的相关性关系
#对member_card和total_children进行分析
sns.boxplot(x=df['member_card'],y=df['total_children'],data=df)
#单因素方差分析
from scipy import stats
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.multicomp import pairwise_tukeyhsd
data=pd.concat([df['member_card'],df['total_children']],axis=1)
model=ols('total_children~C(member_card)',data=data).fit()
anova_result=anova_lm(model)
print(anova_result)
model.summary()