吴恩达机器学习课程笔记+代码实现(12)Python实现多类分类和神经网络(Programming Exercise 3)
Programming Exercise 3:Multi-class Classification and Neural Networks
Python版本3.6
编译环境:anaconda Jupyter Notebook
链接:实验数据和实验指导书
提取码:i7co
本章课程笔记部分见:神经网络:表述(Neural Networks: Representation) 神经网络的学习(Neural Networks: Learning)
本次练习中,我们将使用逻辑回归来识别手写数字(0到9)。 我们将扩展我们在练习2中写的逻辑回归的实现,并将其应用于一对一的分类。
%matplotlib inline
#IPython的内置magic函数,可以省掉plt.show(),在其他IDE中是不会支持的
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="whitegrid",color_codes=True)
import scipy.io as sio
import scipy.optimize as opt
from sklearn.metrics import classification_report#这个包是评价报告
加载数据集和可视化
它是在MATLAB的本机格式,所以要加载它在Python,我们需要使用一个SciPy工具。
data = sio.loadmat('ex3data1.mat')
X = data.get('X')
y = data.get('y')
y = y.reshape(y.shape[0]) # make it back to column vector
data
{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Oct 16 13:09:09 2011',
'__version__': '1.0',
'__globals__': [],
'X': array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]),
'y': array([[10],
[10],
[10],
...,
[ 9],
[ 9],
[ 9]], dtype=uint8)}
print(X.shape,y.shape)
(5000, 400) (5000,)
图像在martix X中表示为400维向量(其中有5,000个)。 400维“特征”是原始20 x 20图像中每个像素的灰度强度。类标签在向量y中作为表示图像中数字的数字类。
def plot_an_image(image):
# """
# image : (400,)
# """
fig, ax = plt.subplots(figsize=(1, 1))
ax.matshow(image.reshape((20, 20)), cmap=mpl.cm.binary)
plt.xticks(np.array([])) # just get rid of ticks
plt.yticks(np.array([]))
#绘图函数
pick_one = np.random.randint(0, 5000)
plot_an_image(X[pick_one, :])
plt.show()
print('this should be {}'.format(y[pick_one]))
this should be 5
def plot_100_image(X):
""" sample 100 image and show them
assume the image is square
X : (5000, 400)
"""
size = int(np.sqrt(X.shape[1]))
# sample 100 image, reshape, reorg it
sample_idx = np.random.choice(np.arange(X.shape[0]), 100) # 100*400
sample_images = X[sample_idx, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
cmap=mpl.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
#绘图函数,画100张图片
plot_100_image(X)
数据预处理
# 同之前的练习一样,add intercept=1 for x0
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1)#插入了第一列(全部为1)
X.shape
(5000, 401)
y
array([10, 10, 10, ..., 9, 9, 9], dtype=uint8)
# 扩展 5000*1 到 5000*10
# 比如 y=10 -> [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]: ndarray
# y have 10 categories here. 1..10, they represent digit 0 as category 10 because matlab index start at 1
# I'll ditit 0, index 0 again
y_matrix = []
for k in range(1, 11):
y_matrix.append((y == k).astype(int))
# last one is k==10, it's digit 0, bring it to the first position,最后一列k=10,都是0,把最后一列放到第一列
y_matrix = [y_matrix[-1]] + y_matrix[:-1]
y = np.array(y_matrix)
y.shape
(10, 5000)
y
array([[1, 1, 1, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 1, 1, 1]])
train 1 model(训练一维模型)
代价函数:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]
#sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
#代价函数
def cost(theta, X, y):
''' cost fn is -l(theta) for you to minimize'''
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
#加入正则化的代价函数
def regularized_cost(theta, X, y, l=1):
'''you don't penalize theta_0'''
theta_j1_to_n = theta[1:]
regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum()
return cost(theta, X, y) + regularized_term
#梯度下降def gradient(theta, X, y):
def gradient(theta, X, y):
'''just 1 batch gradient'''
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
#加入正则化的梯度下降
def regularized_gradient(theta, X, y, l=1):
'''still, leave theta_0 alone'''
theta_j1_to_n = theta[1:]
regularized_theta = (l / len(X)) * theta_j1_to_n
# by doing this, no offset is on theta_0
regularized_term = np.concatenate([np.array([0]), regularized_theta])
return gradient(theta, X, y) + regularized_term
def logistic_regression(X, y, l=1):
"""generalized logistic regression
args:
X: feature matrix, (m, n+1) # with incercept x0=1
y: target vector, (m, )
l: lambda constant for regularization
return: trained parameters
"""
# init theta
theta = np.zeros(X.shape[1])
# train it
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True})
# get trained parameters
final_theta = res.x
return final_theta
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
t0 = logistic_regression(X, y[0])
print(t0.shape)
y_pred = predict(X, t0)
print('Accuracy={}'.format(np.mean(y[0] == y_pred)))
(401,)
Accuracy=0.9974
train k model(训练k维模型)
k_theta = np.array([logistic_regression(X, y[k]) for k in range(10)])
print(k_theta.shape)
(10, 401)
进行预测
- think about the shape of k_theta, now you are making X × θ T X\times\theta^T X×θT
( 5000 , 401 ) × ( 10 , 401 ) . T = ( 5000 , 10 ) (5000, 401) \times (10, 401).T = (5000, 10) (5000,401)×(10,401).T=(5000,10)
- after that, you run sigmoid to get probabilities and for each row, you find the highest prob as the answer
def predict_all(X, all_theta):
rows = X.shape[0]
params = X.shape[1]
num_labels = all_theta.shape[0]
# same as before, insert ones to match the shape
X = np.insert(X, 0, values=np.ones(rows), axis=1)
# convert to matrices
X = np.matrix(X)
all_theta = np.matrix(all_theta)
# compute the class probability for each class on each training instance
h = sigmoid(X * all_theta.T)
# create array of the index with the maximum probability
h_argmax = np.argmax(h, axis=1)
# because our array was zero-indexed we need to add one for the true label prediction
h_argmax = h_argmax + 1
return h_argmax
prob_matrix = sigmoid(X @ k_theta.T)
np.set_printoptions(suppress=True)
prob_matrix
array([[0.99577769, 0. , 0.00053524, ..., 0.00006465, 0.00003907,
0.00172229],
[0.9983465 , 0.0000001 , 0.0000561 , ..., 0.00009675, 0.0000029 ,
0.00008486],
[0.99140504, 0. , 0.0005686 , ..., 0.00000654, 0.02654245,
0.00197582],
...,
[0.00000068, 0.04140879, 0.00320814, ..., 0.0001273 , 0.00297237,
0.70757659],
[0.00001843, 0.00000013, 0.00000009, ..., 0.00164616, 0.0681586 ,
0.86109922],
[0.02879654, 0. , 0.00012981, ..., 0.36617522, 0.0049769 ,
0.14830126]])
y_pred = np.argmax(prob_matrix, axis=1)#返回沿轴axis最大值的索引,axis=1代表行
y_pred
array([0, 0, 0, ..., 9, 9, 7], dtype=int64)
y_answer = data['y'].copy()
y_answer[y_answer==10] = 0
print(classification_report(y_answer, y_pred))
precision recall f1-score support
0 0.97 0.99 0.98 500
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
micro avg 0.94 0.94 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000
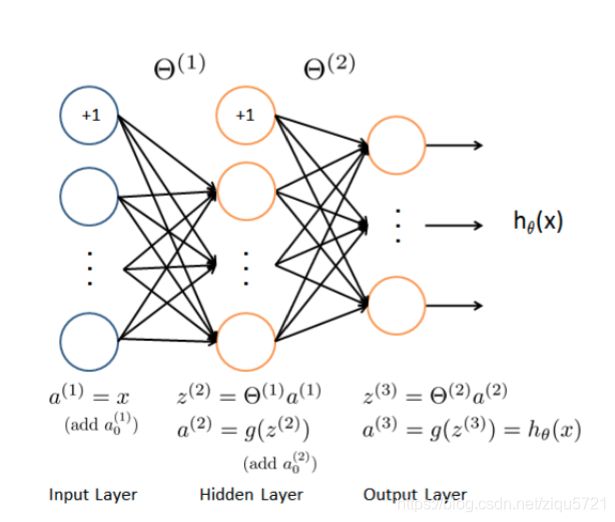
神经网络模型图示
def load_weight(path):
data = sio.loadmat(path)
return data['Theta1'], data['Theta2']
theta1, theta2 = load_weight('ex3weights.mat')
theta1.shape, theta2.shape
((25, 401), (10, 26))
data = sio.loadmat('ex3data1.mat')
X = data.get('X')
y = data.get('y')
y = y.reshape(y.shape[0]) # make it back to column vector
# 同之前的练习一样,add intercept=1 for x0
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1)#插入了第一列(全部为1)
X.shape,y.shape
((5000, 401), (5000,))
feed forward prediction(前馈预测)
a1 = X
z2 = a1 @ theta1.T# (5000, 401) @ (25,401).T = (5000, 25)
z2.shape
(5000, 25)
z2 = np.insert(z2, 0, values=np.ones(z2.shape[0]), axis=1)
a2 = sigmoid(z2)
a2.shape
(5000, 26)
z3 = a2 @ theta2.T
z3.shape
(5000, 10)
a3 = sigmoid(z3)
a3.shape
(5000, 10)
y_pred = np.argmax(a3, axis=1) + 1 # numpy is 0 base index, +1 for matlab convention,返回沿轴axis最大值的索引,axis=1代表行
y_pred.shape
(5000,)
y_pred
array([10, 10, 10, ..., 9, 9, 9], dtype=int64)
准确率
虽然人工神经网络是非常强大的模型,但训练数据的准确性并不能完美预测实际数据,在这里很容易过拟合。
print(classification_report(y, y_pred))
precision recall f1-score support
1 0.97 0.98 0.97 500
2 0.98 0.97 0.97 500
3 0.98 0.96 0.97 500
4 0.97 0.97 0.97 500
5 0.98 0.98 0.98 500
6 0.97 0.99 0.98 500
7 0.98 0.97 0.97 500
8 0.98 0.98 0.98 500
9 0.97 0.96 0.96 500
10 0.98 0.99 0.99 500
micro avg 0.98 0.98 0.98 5000
macro avg 0.98 0.98 0.98 5000
weighted avg 0.98 0.98 0.98 5000