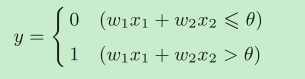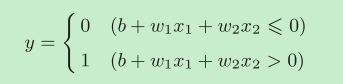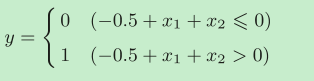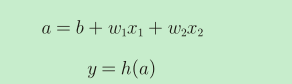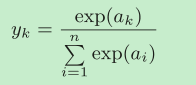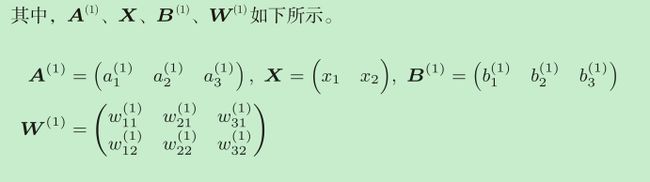Python深度学习入门笔记之1
Python深度学习入门笔记
文章目录
- Python深度学习入门笔记
-
- 1.感知机
-
- 感知机是什么
- 感知机能干什么用
- 导入权重和偏置
- 感知机的局限性
-
- 用图表示感知机实现与门
- 用图表示感知机无法实现与门
- 线性和非线性
- 多层感知机
- 2.神经网络
-
- 在神经元内部明确显示激活函数
- 激活函数
-
- sigmoid函数
-
- 函数图像
- ReLU函数
- softmax函数
-
- softmax函数的特征
- 多维数组的运算
- 神经网络的符号
-
- 输出层的激活函数
- 输出层的神经元数量
1.感知机
感知机是深度学习神经网络的起源算法。
感知机是什么
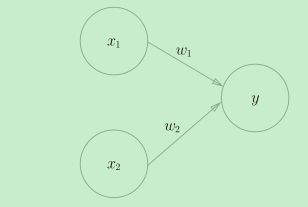
看图
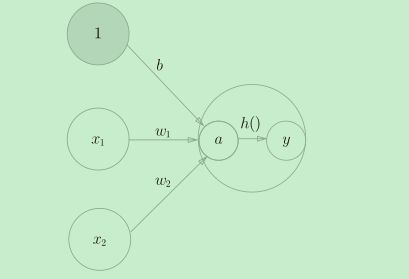
这就是一个两个输入和一个输出的的感知机的例子。其中，x1、x2是输入信号，
y是输出信号，w1、w2是权重（w是weight的首字母），图中的圆圈o被称为**“神经元”或“节点”**。
可以看到，当输入信号被送往神经元时，会分别乘以相应的权重，得到（w1x1，w2x2），而包含y的神经元会计算得到的信号总和，只有当这个总和超过了某个界限值时，才会输出1。这也称为**“神经元被激活”** 。这里将这个界限值称为阈值，用符号θ表示。
也就是
感知机能干什么用
现在让我们考虑用感知机来解决简单的问题。
这里首先以逻辑电路为题材来思考一下与门，其真值表如下图，
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
我们可以将权重和阈值设置为(w1, w2, θ) = (0.5, 0.5, 0.7)，这样就能这个感知机就能完成与门的工作了
0 * 0.5 + 0 * 0.5 = 0 < 0.7 => 0
1 * 0.5 + 0 * 0.5 = 0.5 < 0.7 => 0
0 * 0.5 + 1 * 0.5 = 0.5 < 0.7 => 0
1 * 0.5 + 1 * 0.5 = 1 > 0.7 => 1
实际上与门、与非门、或门的逻辑电路都可以使用感知机表示，更重要的是：与门、与非门、或门的感知机构造是一样的。实际上，3个门电路只有参数的值（权重和阈值）不同。
导入权重和偏置
我们把感知机的换一种方式表述，首先把上式的θ换成−b，b称为偏置。
下面说一下权重w和偏置b的关系：
偏置和权重w1、w2的作用是不一样的。具体地说，w1和w2是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为 1 的程度）的参数。简单来说，如果w1,w2特别大，比如是1000000000，那么x1,x1只需要很小就可以激活神经元。如果b很大，也可以很容易激活神经元。
感知机的局限性
前面介绍的感知机是无法实现异或门。
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
我们从图中或许会看得更清楚一些：
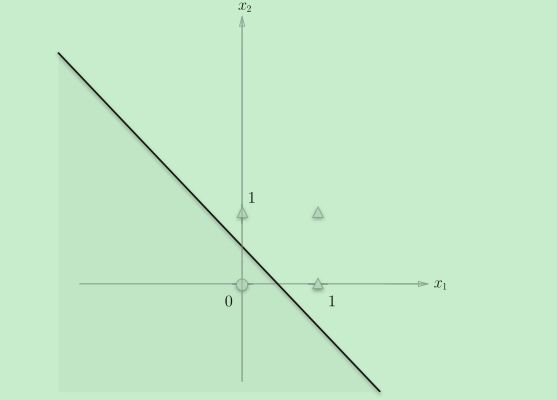
用图表示感知机实现与门
首先，我们将感知机可以表示的与门在图中表示
设权重参数(b, w1, w2) = (−0.5, 1.0, 1.0) （这里是随表给出的参数，只要是能满足与门的参数都可以，而这样的参数有无数个）
感知机表示为
在图中这个感知机表示为将坐标系分割为两部分的一条直线
其中，图标o的坐标是（0,0），而三个△图标的坐标分别是（0,1），（1,0），（1,1），如果我们把坐标位于直线下方定义为输出0，而坐标位于直线上方定义为输出1。这不正是用一条直线（感知机）实现了与门嘛。
| 图标 | x1 | x2 | 位于直线 | y |
|---|---|---|---|---|
| o | 0 | 0 | 下方 | 0 |
| △ | 1 | 0 | 上方 | 0 |
| △ | 0 | 1 | 上方 | 0 |
| △ | 1 | 1 | 上方 | 1 |
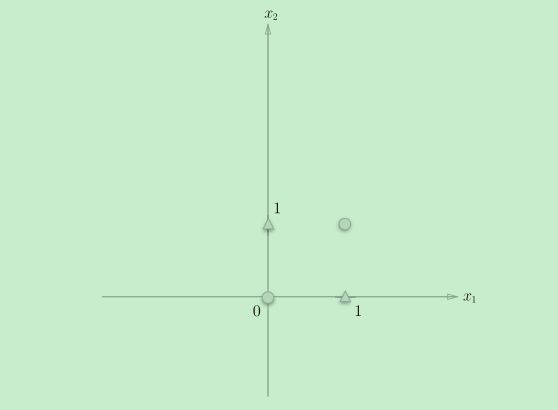
接下来我们看一看异或门在图中是什么情况。
用图表示感知机无法实现与门
异或门中，两个o和两个△无法用一条直线分割，而无论我们将参数设置成什么，我们之前的感知机在图中都只能表示成一条直线，也就是说前面介绍的感知机是无法实现异或门。
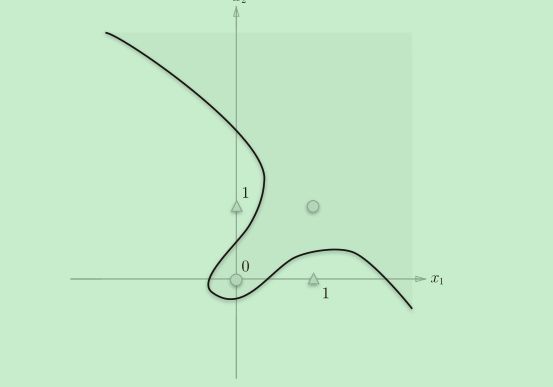
线性和非线性
感知机的局限性就在于它只能表示由一条直线分割的空间。上图这样弯曲的曲线无法用感知机表示。另外，由上图这样的曲线分割而成的空间称为非线性空间，由直线分割而成的空间称为线性空间。
严格地讲，应该是“单层感知机无法表示异或门”或者“单层感知机无法分离非线性空间”。接下来，我们将看到通过组合感知机（叠加层）就可以实现异或门。
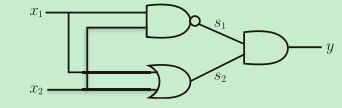
多层感知机
不过感知机最大的神奇之处就在于它可以==“叠加层”==，如果我们有一些简单的电路或逻辑只是，我们就知道通过组合与门、与非门、或门可以实现异或门。
| x1 | x2 | s1 | s2 | y |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
既然我们可以使用单层感知机实现与门、与非门、或门，而通过组合与门、与非门、或门可以实现异或门，那么我们实际上就可以用多层叠加的感知机来实现异或门。
这种叠加了多层的感知机也称为多层感知机（multi-layered perceptron）
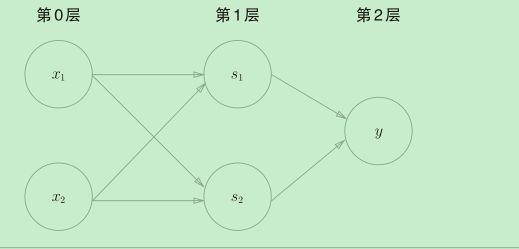
用神经元的形式表示就是这样：
- 第0层的两个神经元接收输入信号，并将信号发送至第1层的神经元。
- 第1层的神经元将信号发送至第2层的神经元，第2层的神经元输出y。
实际上已有研究证明，2层感知机（严格地说是激活函数使用了非线性的sigmoid函数的感知机，具体请参照下一部分）可以表示任意函数。
2.神经网络
书接上文，关于感知机，既有好消息，也有坏消息。好消息是，感知机（理论上）也可以将任何复杂的函数表示出来。而坏消息是，表示这些函数对应的感知机权重参数现在还是由人工进行的。神经网络的出现就是为了解决刚才的坏消息。具体地讲，神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
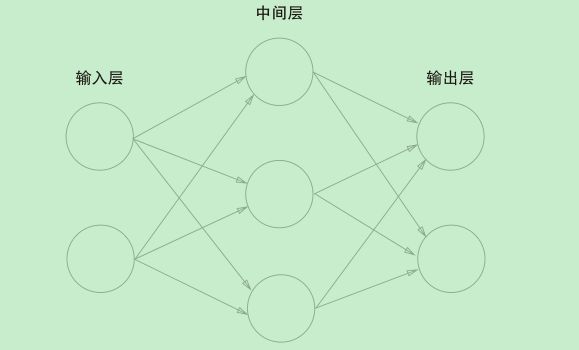
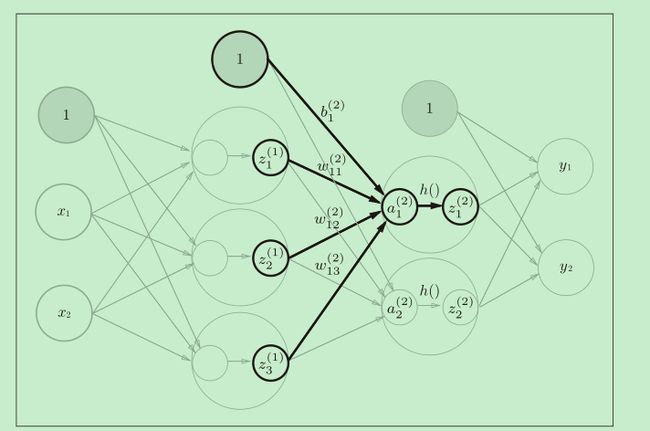
用图来表示神经网络的话，如图 3-1 所示。我们把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层，中间层有时也称为隐藏层。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同）肉眼看不见。
再来复习一下单层感知机
将
这个式子改成更简洁的形式，
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4VAsnmWQ-1640922267823)(E:\胖春college\读书笔记\深度学习入门_鱼书\img\深度学习入门笔记\image-20211231102639065.png)] 一
二
一和二结合就是之前的单层感知机。
在神经元内部明确显示激活函数
刚才登场的**h（x）**函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。如“激活”一词所示，激活函数的作用在于决定如何来激活输入信号的总和。
再把式子一拆分成两部分：
最终在图上表示出：
激活函数
上面我们使用的激活函数h(x)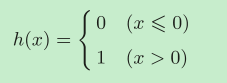非常简单，它以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为**“阶跃函数”**。
实际上，如果将激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界了。
sigmoid函数
神经网络中经常使用的一个激活函数就是sigmoid函数。
exp(−x)表示e-x的意思。
在神经网络中就是用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。
函数图像
可以看到阶跃函数和sigmoid函数的图像。
sigmoid函数是一条平滑的曲线，输出随着输入发生连续性的变化。而阶跃函数以0为界，输出发生急剧性的变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。
阶跃函数和sigmoid函数两者均为非线性函数。
神经网络的激活函数必须使用非线性函数。因为如果使用线性函数的话，加深神
经网络的层数就没有意义了。为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。
ReLU函数
在神经网络发展的历史上，除了sigmoid函数还有ReLU（Rectified Linear Unit）函数。
ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。
softmax函数
softmax函数的分子是输入信号ak的指数函数，分母是所有输入信号的指数
函数的和。
softmax函数的输出通过箭头与所有的输入信号相连。从式子可以看出，输出层的各个神经元都受到所有输入信号的影响。
softmax函数的特征
softmax函数的输出是0.0到1.0之间的实数。并且，softmax函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。
比如，上面的例子可以解释成y[0]的概率是0.018（1.8 %），y[1]的概率
是 0.245（24.5 %），y[2]的概率是 0.737（73.7 %）。从概率的结果来看，可以
说“因为第2个元素的概率最高，所以答案是第2个类别”！！！！
也就是说，通过使用softmax函数，我们可以用概率的（统计的）方法处理问题。
一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且，即便使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，输出层的softmax函数可以省略（为了减少计算量）
多维数组的运算
使用NumPy多维数组的运算，就可以高效地实现神经网络。
二维数组也称为矩阵（matrix）。通过矩阵的乘积可以高效的实现神经网络的计算。
将输入值x1,x1当成一个1 * 2的矩阵1，权重 w1w2w3w4w5w6当成一个2 * 3的矩阵2（具体是几乘几的额矩阵要看神经网络的各层之间是怎样连接的）
那么输出值y1,y2,y3组成的矩阵3就是矩阵1和矩阵2的乘积。
神经网络的符号
a1(1)的计算方式：
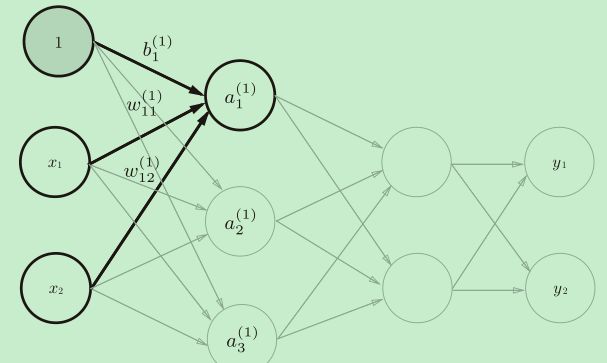
用矩阵表示：A(1)= X W(1)+ B(1)
输出层的激活函数
输出层的激活函数用σ()表示，不同于隐藏层的激活函数h()（σ读作sigma）。
输出层所用的激活函数，要根据求解问题的性质决定。
一般地，回归问题可以使用恒等函数，二元分类问题可以使用sigmoid函数，多元分类问题可以使用softmax函数。
#初始化每一层的权重和偏置
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
#将输入信号转换为输出信号的处理过程
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
#第0层->第一层
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
#第一层->第二层
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
#第二层->输出层
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
#获取参数
network = init_network()
#输入值
x = np.array([1.0, 0.5])
#计算输出值
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]
输出层的神经元数量
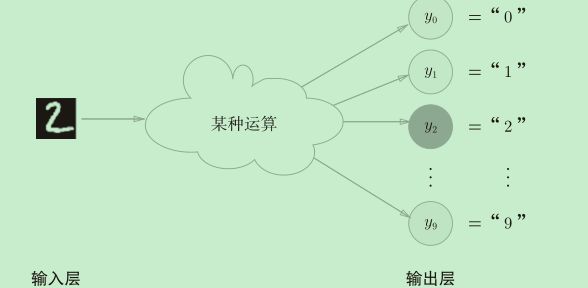
输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量，需要分成几类，就把输出层神经元设置成几个。
在这个例子中，输出层的神经元从上往下依次对应数字0, 1, . . ., 9。在输出层，“2”输出值最大（用颜色重表示），因此这个神经网络预测出输入的图片的值是“2”。！！
求解机器学习问题的步骤可以分为**“学习”和“推理”两个阶段**。首先，在学习阶段进行模型的学习（学习出最合适的权重值），然后，在推理阶段，用学到的模型对未知的数据进行推理（分类）。神经网络也是一样。！！