线性回归预测波士顿房价
一、实验目的
1.理解线性回归的基本原理,掌握基础的公式推导。
2.能够利用公式手动实现LinearRegression中的fit和predict函数。
3.能够利用自己实现的LinearRegression和sklearn里的LinearRegression进行波士顿房价预测,并比较2个模型结果差异。
二、实验内容
2.1 实现LinearRegression
根据下面公式可以利用训练集得到权重w
w = ( x T x ) − 1 x T y w=(x^Tx)^{-1}x^Ty w=(xTx)−1xTy
代码:
class LinearRegression_writing():
def __init__(self, l):
self.w = None
self.l = l
def fit(self, x, y):
t = x.shape[1]
x = np.insert(x, len(x[0]), 1, 1)
t_1 = np.dot(np.transpose(x), x) + self.l*np.eye(t+1)
u, s, v = np.linalg.svd(t_1, full_matrices=False)
inv = np.matmul(v.T*1/s, u.T)
t_2 = np.dot(inv, np.transpose(x))
self.w = np.dot(t_2, y)
def predict(self, test_x):
test_x = np.insert(test_x, len(test_x[0]), 1, 1)
pred_y = np.dot(test_x, self.w)
return pred_y
2.2 波士顿房价预测
2.2.1 导入模块
首先我们导入必要的库:
import numpy as np
import pandas as pd
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn.metrics import mean_squared_error, r2_score
2.2.2 加载数据集
我们直接从github上读取csv文件
dataset = pd.read_csv("https://raw.githubusercontent.com/selva86/datasets/master/BostonHousing.csv", thousands=',')
2.2.3 数据预处理
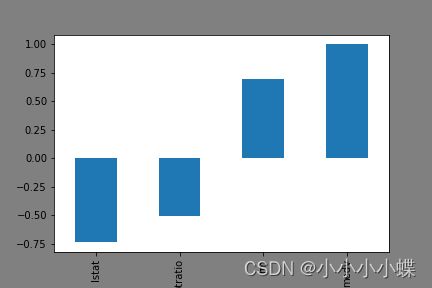
1.将每一个和房价的相关系数大于0.5的特征画图显示出来
dataset.corr()['medv']
plt.figure(facecolor='gray')
corr = dataset.corr()
corr = corr['medv']
corr[abs(corr) > 0.5].sort_values().plot.bar()
2.只选取相关系数大于0.5的特征,去掉剩余特征
dataset = dataset[['lstat','ptratio','rm','medv']]
y = dataset['medv']
x = dataset.drop('medv', axis=1)
3.使用KFold交叉验证划分数据集和测试集
此处,我们选择划分层数为5,同时保留数据集排序中的顺序依赖关系
kfolds = KFold(n_splits=5, shuffle=False)
for i, j in kfolds.split(x, y):
X_train, X_test = x.iloc[i], x.iloc[j]
y_train, y_test = y.iloc[i], y.iloc[j]
X_train = np.array(X_train)
X_test = np.array(X_test)
y_train = np.array(y_train)
y_test = np.array(y_test)
4.数据归一化
由于各维属性的取值范围差别很大,需要进行数据归一化操作,这里我们使用一种很常见的操作方法:减掉均值,然后除以原取值范围。
做归一化至少有以下3个理由:
- 过大或过小的数值范围会导致计算时的浮点上溢或下溢。
- 不同的数值范围会导致不同属性对模型的重要性不同,而这个隐含的假设常常是不合理的。这会对优化的过程造成困难,使训练时间大大的加长。
- 很多的机器学习技巧/模型(例如L1,L2正则项,向量空间模型-Vector Space Model)都基于这样的假设:所有的属性取值都差不多是以0为均值且取值范围相近的。
# 初始化标准化器
min_max_scaler = preprocessing.MinMaxScaler()
# 分别对训练和测试数据的特征以及目标值进行标准化处理
X_train = min_max_scaler.fit_transform(X_train)
y_train = min_max_scaler.fit_transform(y_train.reshape(-1,1)) # reshape(-1,1)指将它转化为1列,行自动确定
X_test = min_max_scaler.fit_transform(X_test)
y_test = min_max_scaler.fit_transform(y_test.reshape(-1,1))
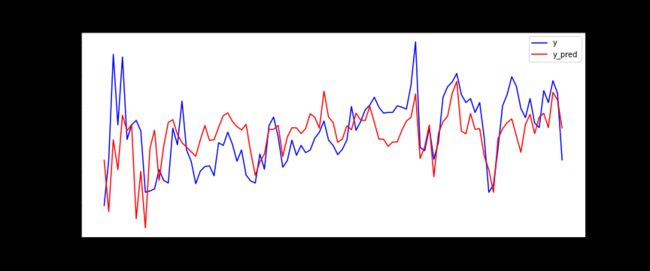
2.2.4 训练模型并预测
自己实现的算法:
model = LinearRegression_writing(0.1)
model.fit(X_train, y_train)
y_test_pred_writing = model.predict(X_test)
linear_model:
lr = LinearRegression()
lr.fit(X_train, y_train)
MSETest = mean_squared_error(y_test, y_test_pred)
2.2.5 评估模型
自己实现的算法:
linear_model:
| MSE | MAE | R^2 | |
|---|---|---|---|
| me_model | 0.03320945721623632 | 0.14872295006769706 | 0.23180001594027266 |
| linear_model | 0.0333506675540496 | 0.14902746967046934 | 0.2285335434246003 |
三、实验总结
实验过程中在实现fit和predict函数过程中遇到了一些困难,原因是对numpy的各种用法还不够熟练,今后要加强熟练程度。在实现过程中,加入了正则化惩罚因子,从MSE、MAE、R^2各项评估指标来看,自己实现的模型要比linear_model结果好一些。通过本次实验,加强了对线性回归的理解,深入了解了其内部的原理,希望后面实验中能学到更多的方法。