深度学习之图像分类（十四）--ShuffleNetV2 网络结构

深度学习之图像分类（十四）ShuffleNetV2 网络结构

本节学习 ShuffleNetV2 网络结构。学习视频源于 Bilibili，感谢霹雳吧啦Wz，建议大家去看视频学习哦。

1. 前言

ShuffleNetV2 是由国产旷视科技团队在 2018 年提出的，发表在了 ECCV，其原始论文为 ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design。这篇文章非常硬核，实验非常全面。在 ShuffleNetV2 论文中作者提到了，计算复杂度不能只看 FLOPs，为此提出了 4 条设计高效网络的准则，基于准则提出了新的 block 设计。

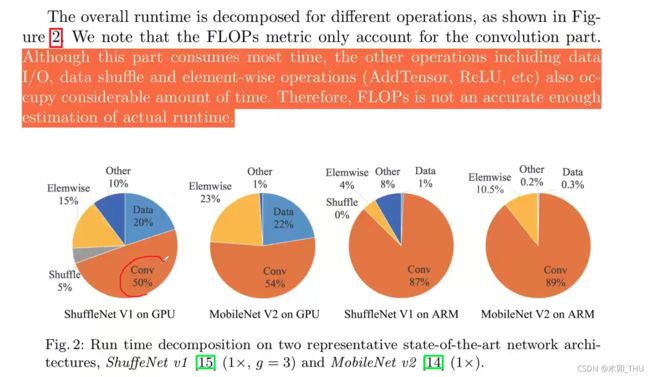
首先看一下论文中给的一些论述，在 MobileNet，ShuffleNetV1 中经常讲的是 FLOPs，其实是衡量模型运算或者复杂度的一个间接的指标，并不是直接的指标。在直接使用过程中我们都是通过 Speed 看推理速度。所以在影响模型推理速度的众多因素中间，我们不能光看 FLOPs，还要考虑其他因素例如内存访问时间成本 MAC (memory access cost)。此外，并行等级 degree of parallelism 也是需要考虑的。相同的 FLOPs 在不同的平台上计算时间也是不同的。

通过下图能发现，我们的卷积还是占据了模型推理的绝大部分时间，但是其他操作例如 data 的 I/O，shuffle 等也占据了相当大的一部分时间。因此 FLOPs 并不能准确评判模型的执行时间。

2. Several Practical Guidelines for Efficient Network Architecture Design

为此作者给出了四条设计高效网络的准则，包括：

• G1: Equal channel width minimizes memory access cost (MAC).
• G2: Excessive group convolution increases MAC.
• G3: Network fragmentation reduces degree of parallelism.
• G4: Element-wise operations are non-negligible.

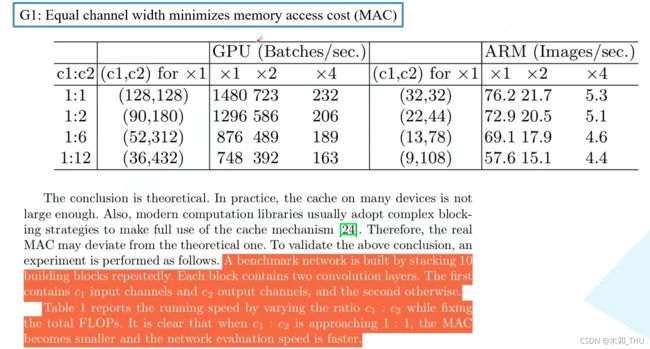
2.1 Equal channel width minimizes memory access cost (MAC).

Guideline1 中作者提到，当卷积层输入特征矩阵与输出特征矩阵 channel 相等时，MAC 最小（保持 FLOPs 不变时）。这里主要是针对 $1\times 1$ 的卷积层，$hw{c}_1$ 是输入特征矩阵的内存消耗，$hw{c}_2$ 是输出特征矩阵的内存消耗，$1\times 1\times c_1{c}_2$ 是卷积核参数的内存消耗。由于我们的条件是 FLOPs 即 B 保持不变，使用均值不等式可以算出如下式子，取等条件是 $c_1=c_2$。

基于这个准则作者做了一系列实验，在实验中作者简单堆叠一系列 block（每个 block 两个卷积层，第一个输入通道是 $c_1$，输出通道是 $c_2$，第二个反过来），在保持 FLOPs 不变的情况下，$c_1:c_2=1:1$ 的时候在 GPU 上能每秒运算 1480 个 Batches，随着 $c_1,c_2$ 比值相差越来越大，推理速度越来越慢。在 ARM 中规律是一样的。

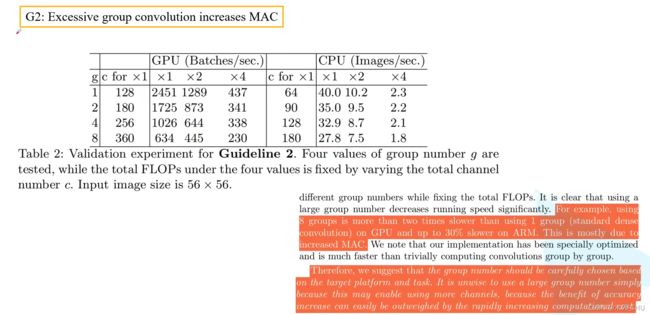
2.2 Excessive group convolution increases MAC.

Guideline2 中作者提到，当 Group Conv 的 groups 增大时，MAC 也会增大（保持 FLOPs 不变时）。对于 Group Conv，这里主要是针对 $1\times 1$ 的卷积层，$hw{c}_1$ 是输入特征矩阵的内存消耗，$hw{c}_2$ 是输出特征矩阵的内存消耗，$1\times 1\times (c_1/g)\times (c_2/g)\times g$ 是卷积核参数的内存消耗。当固定 FLOPs 即 B 保持不变时，可见 g 增大会造成 MAC 增大。

作者针对第二点也进行了一系列实验。保持 FLOPs 不变时，可见随着 g 的增加，GPU 和 CPU 每秒处理的图片数量不断降低。

2.3 Network fragmentation reduces degree of parallelism.

Guideline3 中作者提到，当网络设计的碎片化程度越高时，推理速度越慢。很多论文中设计的网络，分支特别多，例如 Inception，SPP block 等。这里碎片化的程度可以理解为分支的程度。这个分支可以是串联也可以是并联。虽然碎片化的结构可以提升准确率，但是会降低模型的效率。碎片化的结构对于 GPU 这种并行能力强的设备是很不友好的。并且在分支多的情况下还涉及 kernel 的起步和同步的问题。右侧表格的每一行对应于左下角的每一种情况，在 GPU 上符合理论，但是 CPU 上怎么反而还快了一点点，这也说明不同设备在运行相同结构之间的差异。

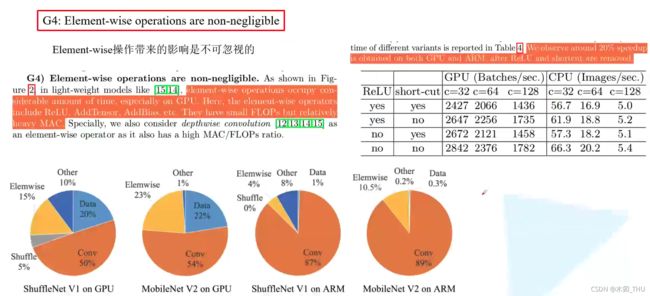
2.4 Element-wise operations are non-negligible.

Guideline4 中作者提到，Element-wise 操作带来的影响不可忽视。Element-wise 操作包括激活函数，元素加法 (残差结构)，卷积中的 bias。Element-wise 操作的共性是 FLOPs 很小，但是 MAC 很大。此外，DW conv 其实也可以看作是 Element-wise 操作。一系列的实验表明，不采用 short-cut 连接会更快，不采用 ReLU 会比采用 ReLU 快。有人会说，不用肯定会快呀，这里作者想要突出的是，Element-wise 操作比想象中更耗时。作者提到，如果将 short-cut 和 ReLU 都移除会有 20% 的加速。如果只看 FLOPs 的话会认为这些操作并不怎么占用时间。

2.5 总结

基于上述四条分析，作者提出了总结：

• 使用 “平衡” 的卷积，即尽可能让输出输出 channel 的比值为 1
• 注意 Group Conv 的计算成本，并不能一昧地增大 Group 数量
• 降低网络的碎片成程度
• 尽可能减少 Element-wise 操作

3. ShuffleNetV2 中的 block

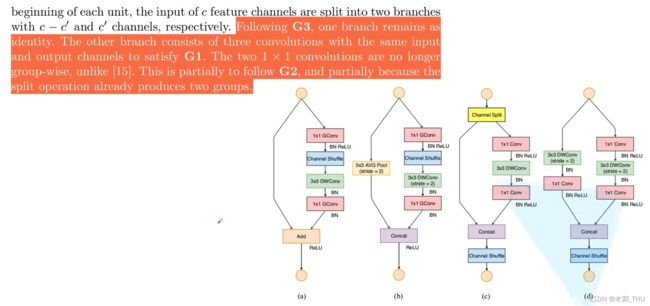
下图中左边的 a 和 b 分别对应 ShuffleNetV1 中 stride = 1 和 stride = 2 的情况，右边的 c 和 d 分别对应 ShuffleNetV2 中 stride = 1 和 stride = 2 的情况。

针对 c 类型的 block，首先对于每个 block 单元，将输入特征矩阵的通道 c 拆分为两个分支 c - c‘ 和 c’，即对应着 channel split。作者在论文中说了 $c^{\prime }=c/2$。针对 G3，我们减少碎片化程度，所以在左边分支不做事情，右边的分支三个卷积输入输出通道数都是一样的，满足了 G1。两个 $1\times 1$ 卷积不再使用 Group conv，这也是为了满足 G2。 在卷积之后，两个分支是通过 Concat 进行通道拼接，这也就使得 block 前后通道数保持不变，也满足 G1。然后在 block 中后进行 channel shuffle。在 © 中不再有 Add 操作，ReLU 和 DW Conv 也只在一个分支中存在（a 中 Add 之后的 ReLU 放到了 c 中最后一个 $1\times 1$ 卷积之后，处理的元素数目少了一半），尽可能减少了Element-wise 操作。然后最后的 Concat，Channel Shuffle 以及接下来的 Channel Split 其实可以合并为一次 Element-wise 操作，变相减少了 Element-wise 操作，符合 G4。

针对 d 类型的 block，即下采样的情况，就没有了 channel split 操作，最后 Concat 之后输出特征矩阵的 channel 就翻倍了。并且将 b 中一个分支的 $3\times 3$ 平均池化变为了 $3\times 3$ 的 DW conv，本来平均池化就是分通道做的，并且可以看成是权重全是 1/9 的 DW Conv，这里换为了 DW Conv 增加了更多的可能。然后再新增了一个 $1\times 1$ 卷积。

注意 DW 卷积之后是只有 BN 没有 ReLU 的哟。

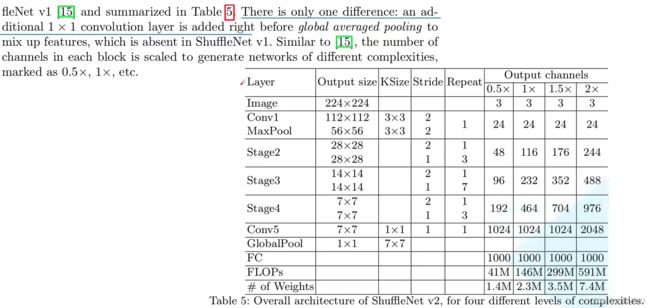
4. ShuffleNetV2 网络结构

ShuffleNetV2 和 ShuffleNetV1 框架基本都是一样的，唯一的不同在于多了一个 Conv5 这个 $1\times 1$ 卷积层。对于每个 stage 的第一个 block，stride 都是 2 ，输出 channel 是需要进行翻倍的。此外对于 stage2 的第一个 block，他的两个分支中输出的 channel 并不等于输入的 channel，而是直接设置为指定输出 channel 的一半，比如对于 1x 版本，每个分支的 channel 应该是 58 而不是 24。

为什么要加 Conv5 呢？知乎上看到一个狗头回答 ：

为什么要加conv5呢？猜，不加准确率保证不了，不然比起v1版本减去那么多的 groups，速度是上去了准确率是万万不能下去的，怎么办呢？再加一层卷积试试吧。

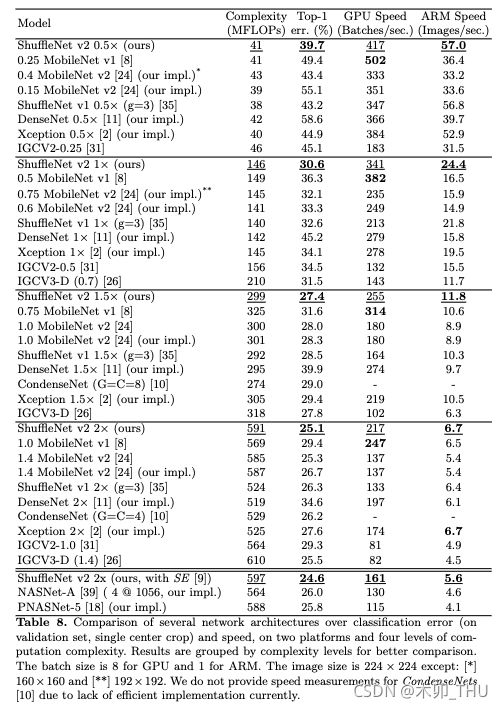
最后看一下 ShuffleNetV2 的性能指标，大家的 FLOPs 差不多，但是 ShuffleNetV2 的正确率和速度都很不错啊：

其实 ShuffleNetV2 还可以搭配 SE 注意力模块，作者在论文中给出了实验结果，其正确率和速度都是最优的：

5. 代码

ShuffleNetV2 实现代码如下所示，代码出处：

from typing import List, Callable

import torch
from torch import Tensor
import torch.nn as nn


def channel_shuffle(x: Tensor, groups: int) -> Tensor:

    batch_size, num_channels, height, width = x.size()
    channels_per_group = num_channels // groups

    # reshape
    # [batch_size, num_channels, height, width] -> [batch_size, groups, channels_per_group, height, width]
    x = x.view(batch_size, groups, channels_per_group, height, width)

    x = torch.transpose(x, 1, 2).contiguous()

    # flatten
    x = x.view(batch_size, -1, height, width)

    return x


class InvertedResidual(nn.Module):
    def __init__(self, input_c: int, output_c: int, stride: int):
        super(InvertedResidual, self).__init__()

        if stride not in [1, 2]:
            raise ValueError("illegal stride value.")
        self.stride = stride

        assert output_c % 2 == 0
        branch_features = output_c // 2
        # 当stride为1时，input_channel应该是branch_features的两倍
        # python中 '<<' 是位运算，可理解为计算×2的快速方法
        assert (self.stride != 1) or (input_c == branch_features << 1)

        if self.stride == 2:
            self.branch1 = nn.Sequential(
                self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),
                nn.BatchNorm2d(input_c),
                nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
                nn.BatchNorm2d(branch_features),
                nn.ReLU(inplace=True)
            )
        else:
            self.branch1 = nn.Sequential()

        self.branch2 = nn.Sequential(
            nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,
                      stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True),
            self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),
            nn.BatchNorm2d(branch_features),
            nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True)
        )

    @staticmethod
    def depthwise_conv(input_c: int,
                       output_c: int,
                       kernel_s: int,
                       stride: int = 1,
                       padding: int = 0,
                       bias: bool = False) -> nn.Conv2d:
        return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,
                         stride=stride, padding=padding, bias=bias, groups=input_c)

    def forward(self, x: Tensor) -> Tensor:
        if self.stride == 1:
            x1, x2 = x.chunk(2, dim=1)
            out = torch.cat((x1, self.branch2(x2)), dim=1)
        else:
            out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)

        out = channel_shuffle(out, 2)

        return out


class ShuffleNetV2(nn.Module):
    def __init__(self,
                 stages_repeats: List[int],
                 stages_out_channels: List[int],
                 num_classes: int = 1000,
                 inverted_residual: Callable[..., nn.Module] = InvertedResidual):
        super(ShuffleNetV2, self).__init__()

        if len(stages_repeats) != 3:
            raise ValueError("expected stages_repeats as list of 3 positive ints")
        if len(stages_out_channels) != 5:
            raise ValueError("expected stages_out_channels as list of 5 positive ints")
        self._stage_out_channels = stages_out_channels

        # input RGB image
        input_channels = 3
        output_channels = self._stage_out_channels[0]

        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, stride=2, padding=1, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )
        input_channels = output_channels

        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)

        # Static annotations for mypy
        self.stage2: nn.Sequential
        self.stage3: nn.Sequential
        self.stage4: nn.Sequential

        stage_names = ["stage{}".format(i) for i in [2, 3, 4]]
        for name, repeats, output_channels in zip(stage_names, stages_repeats,
                                                  self._stage_out_channels[1:]):
            seq = [inverted_residual(input_channels, output_channels, 2)]
            for i in range(repeats - 1):
                seq.append(inverted_residual(output_channels, output_channels, 1))
            setattr(self, name, nn.Sequential(*seq))
            input_channels = output_channels

        output_channels = self._stage_out_channels[-1]
        self.conv5 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )

        self.fc = nn.Linear(output_channels, num_classes)

    def _forward_impl(self, x: Tensor) -> Tensor:
        # See note [TorchScript super()]
        x = self.conv1(x)
        x = self.maxpool(x)
        x = self.stage2(x)
        x = self.stage3(x)
        x = self.stage4(x)
        x = self.conv5(x)
        x = x.mean([2, 3])  # global pool
        x = self.fc(x)
        return x

    def forward(self, x: Tensor) -> Tensor:
        return self._forward_impl(x)


def shufflenet_v2_x1_0(num_classes=1000):
    """
    Constructs a ShuffleNetV2 with 1.0x output channels, as described in
    `"ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design"
    `.
    weight: https://download.pytorch.org/models/shufflenetv2_x1-5666bf0f80.pth
    :param num_classes:
    :return:
    """
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 116, 232, 464, 1024],
                         num_classes=num_classes)

    return model


def shufflenet_v2_x0_5(num_classes=1000):
    """
    Constructs a ShuffleNetV2 with 0.5x output channels, as described in
    `"ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design"
    `.
    weight: https://download.pytorch.org/models/shufflenetv2_x0.5-f707e7126e.pth
    :param num_classes:
    :return:
    """
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 48, 96, 192, 1024],
                         num_classes=num_classes)

    return model