决策数算法进阶：属性测试条件、最佳划分度量、过拟合现象的处理

我们在先前博文中已经简要介绍了决策树的思想和几个经典算法来构造决策树：《决策树算法简介及其MATLAB实现代码》。今天我们要针对决策树继续深入探讨一些的问题，目录如下：

目录

一、表示属性测试条件的方法

二、选择最佳划分的度量

三、处理决策树归纳中的过分拟合现象

---

一、表示属性测试条件的方法

决策树在增长过程中的每个递归步都要选择一个属性测试条件，将数据划分成更小的子集。为了实现这个步骤，算法必须为不同类型的属性指定测试条件的方法及其相应的输出方法。

二元属性

二元属性的测试条件产生两个可能的输出，如下图所示。

标称属性

有多个属性值，测试条件可以用两种方法表示：多路划分和二元划分。在某些决策树算法如CART中，只产生二元划分，所以我们需要在有多个属性值的情况下也支持或者说提供二元划分的方法。

序数属性

也可以产生二元或者多路划分，只要不违背数据属性值的有序性。如下图所示是序数属性的不同的分组方式。

连续属性

对于连续属性来说，测试条件可以是具有二元输出的比较测试结果（即构造大于、小于表达式的结果，真或假），也可以是一个基于范围的输出。

对于多路划分，算法必须考虑所有可能的连续值区间。可以使用之前介绍的离散化策略（《数据预处理工作中的几个关键主题探讨：聚集、抽样、降维、离散化、变量变换等》），离散化之后每隔离散化区间赋予一个新的序数值，只要保持有序性，相邻的值还可以聚集成更宽的区间。

二、选择最佳划分的度量

有很多度量可以用来确定划分数据的最佳方法。

选择最佳划分的度量通常是根据划分后子女结点不纯性的程度。不纯的程度越低，类分布就越倾斜。

不纯性度量包括：

当选择熵（entropy）作为不纯性度量时，熵的差就是所谓的信息增益（information gain），这是后话。

c表示类别数。举个例子，分别对三个结点计算上面式子表示的不纯性度量：

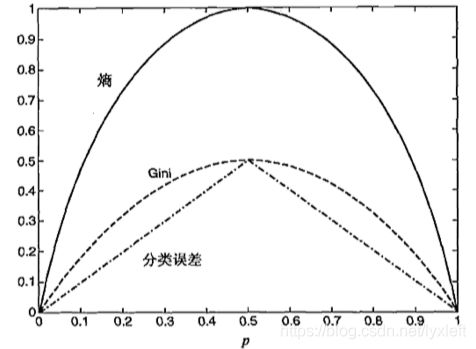
可以看出，三种方法都是在类分布均衡时（概率分布为0.5和0.5）达到最大，而当所有数据都属于同一个类时（即概率分布为0和1），达到最小值。他们的度量结果是一致的。其曲线我们画出来就是：

我们比较父结点和子结点的不纯成都，差越大，测试条件的效果就越好。增益delta△是一种可以用来确定划分效果的标准：

I是不纯性度量，N是父结点上数据总数，k是属性值的个数，N（vj）是与子结点vj相关联的记录个数。决策树算法通常选择最大化增益△的方法来确定测试条件，因为对于所有的测试条件来说，I(parent)是一个不变的值，所以最大化增益等价于最小化子女结点不纯度的加权平均值！

多路划分的不纯性度量往往比二元分化小，因为二元划分实际上合并了多路划分的某些输出，降低了子集的纯度。

以上介绍偏理论，大家可以寻找一些决策树的实例来辅助理解。

改进评价标准——增益率

不纯性度量有利于具有大量不同值的属性。然而，有些情况下，比如用ID来分类人，那么纯度是很高的，因为ID和人一一对应。但是这样就会划分成非常多路，即产生大量输出的测试条件，因为每个划分都是唯一的， 相关联记录太少，以致于不能依此做出可靠的预测。

解决该问题的策略有两种：

1、限制测试条件只能是二元划分，如CART算法。

2、修改评估划分的标准，把属性测试条件产生的输出数也考虑进去。如C4.5算法中用“增益率（gain ratio）”来作为评估划分的标准。

其中，划分信息:，k是划分的总数。如果某个属性产生了大量的划分，它的划分信息将会很大，从而降低了增益率。

三、处理决策树归纳中的过分拟合现象

先剪枝（提前终止规则）

在决策树完全拟合整个训练数据集之前就停止决策树的生长。采用更具限制性的结束条件，比如当不纯性度量的增益或估计的泛化误差的改进低于某个确定的阈值时就停止扩展叶结点。当然，这种依靠阈值的方法，很难保证结果是最优的。

后剪枝

先放任决策树按最大允许的规模生长，然后进行剪枝操作，按照自底向上的方式修剪完全增长的决策树。

修剪的方法有两种：1、用新的叶结点替换子数。该叶子结点的类标号由下面子树记录中的多数类确定。也就是说不管下面多少分叉，都剪掉，按照少数服从多数原则直接决定该结点的类别。就像葡萄一样，直接撸走一子串，撸走的部位的性质根据这个子串里的葡萄性质来定；2、用子树中最常用的分支代替子树。

当模型不能再改进时，终止剪枝步骤。

与先剪枝相比，后剪枝技术倾向于产生更好的效果。因为先剪枝是无先验知识的，而后剪枝是已经大致观览了决策树的全貌再做决定。但是后剪枝计算消耗更大，而且剪掉就浪费了。所以还是要权衡二者的使用。