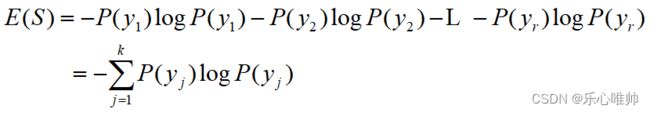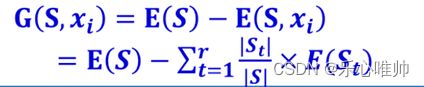【人工智能】期末复习 重点知识点总结
试卷共有15道题,四种题型:
1、名词解释题(不超过五个字的概念)
2、简答题(包涵计算)
鲁滨逊归结原理、wuzi?置换?
- 倒推值计算方法、
- 代价树每个结点的代价的算法:最大代价法、和代价法
- α-β剪枝、
3、证明题
4、综合题
小小tips
理解就可、不用和课本一模一样、说的正确就行
千万别空着,有步骤分、可以找分
书、课后习题、itc习题多看看
老师没有讲的 就不考
一、知识表示的基本方法
非结构化方法:一阶谓词逻辑,产生式规则
结构化方法:语义网络,框架
其他方法:状态空间法,问题规约法
二、人工智能三大流派
(1)符号主义学派:
认识的基元是符号,认识过程就是符号运算和推理;
代表人物:纽厄尔,西蒙;
代表成果:人工定理证明,人工智能语言LISP,鲁滨逊归结原理,专家系统。
(2)连接主义学派:
思维的基元是神经元,而不是符号,思维的过程是神经元的连接活动,而不是符号运算的过程;
代表人物:麦卡洛克,霍普菲德尔;
代表成果:单层感知机,Hopfield网络,BP网络。
(3)行为主义学派,
行为主义学派认为人工智能起源于控制论,智能取决于感知与行为,取决于对外部复杂环境的适应;
代表任务及成果:布鲁克斯研制的六角机器虫。
三、合一置换
置换的例题
合一置换的概念与计算方法
二元归结式证明过程
四、产生式表示法(不确定性推理方法里的说法)
1、产生式系统的组成
(1)一个综合数据库,又称事实库,用于存放输入的事实,从外部数据库输入的事实、中间结果、最后结果;
(2)一组产生式规则,描述某领域内知识的产生式集合;
(3)一个控制系统,包含推理方式和控制策略,又称推理机或推理引擎。
2、专家系统推理过程和结果
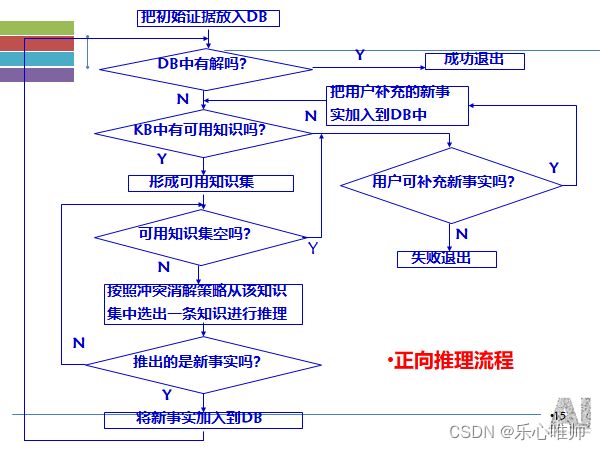
3、正向推理
也称为数据驱动推理或前向链推理
4、逆向推理
亦称为目标驱动推理或逆向链推理
5、知识匹配
五、框架、语义网
(了解如何构建)
框架:横向、纵向联系
匹配、继承方法
有例题
六、状态空间图
构建状态空间图来问题求解 盲目搜索 得到解、如何表示出来
七、与或图:搜索
1、搜索的概念
依靠经验,利用已有知识,根据问题的实际情况,不断寻找可利用知识,从而构造一条代价最小的推理路线,使问题得以解决的过程称为搜索。
2、启发式搜索与盲目性搜索的区别
(1)盲目搜素是指在搜索之前就预定好控制策略,整个搜索过程中的策略不变,即使搜索出来的中间信息有利用价值,其搜索过程中的策略不再改变,效率低,灵活性差,不利于复杂问题求解。
(2)智能搜索是指可以利用搜索过程中得到的中间信息(与问题相关的信息)来引导搜索过程向最优方向发展的算法。
3、启发式信息的概念、(简答、名词解释)
用于指导搜索过程且与具体问题求解有关的控制信息称为启发信息
启发信息作用分类:
- 用于决定先扩展哪一个节点
- 在扩展节点时,用于决定要生成哪一个或哪几个后继节点
- 用于确定某些应该从搜索树中抛弃或修建的节点
4、启发函数的概念
在扩展节点时,用来描述节点重要程度的函数称为估价函数, 一般形式为f(x)=g(x)+h(x)。其中,g(x)为初始节点S0到节点x已实际付出的代价,h(x)是从节点x到目标节点Sg的最优路径的估计代价,启发信息主要由h(x)来体现,故把它称为启发函数。
5、A算法和A*算法基本原理和区别
A算法
在状态空间搜索中,如果每一步都利用估价函数f(n)=g(n)+h(n)对Open表中的节点进行排序,则称为A算法。它是一种为启发式搜索算法
类型:
全局择优:从Open表中的所有节点中选择一个估价函数值最小的进行扩展
局部择优:仅从刚生成的子节点中选择一个估价函数值最小的进行扩展。
A*算法
对在A算法的基础上,选用了一个比较特殊的估价函数,对节点n定义f*(x)=
g*(x)+h*(x),表示从S0开始通过节点x到Sg的一条最佳路径的代价,g是g*的估计,h是h*的估计。g(x)是对最小代价g*(x)的估计,且g(x)>0,g(x)>=g*(x),
h(x)为h*(x)的下界,即对所有的x存在h(x)<=h*(x)
八、与或树
1、与或树的有序搜索
盲目搜索:没有考虑代价,所求得的解树不一定是代价最小的解树,即不是最优解树。
启发式搜索:要多看几步,计算一下扩展一个节点可能要付出的代价,以选择代价最小的节点进行扩展。
2、希望树的概念
在有序搜索中,应选择那些最有希望成为最优解树一部分的节点进行扩展。我们称这些节点构成的树为希望树。
全局择优、基于希望树的搜索???
3、解树的代价计算
最大代价法计算、和代价法计算
九、博弈树(很重要):
1、博弈树的概念
在博弈过程中,已方的各种攻击方案为“或”关系,而对方的应着方案为“与”关系。描述博弈过程的“与/或”树称为博弈树。
根节点是初始状态
2、极大极小分析法(很重要)
- 若父节点为“或”节点,则其分数等于其所有子节点分数的最大值。
- 若父节点为“与”节点,则其分数等于其所有子节点分数的最小值。
- 计算出的父节点的分数值称为倒推值。
- 如果一个方案能获得较大的倒推值,则它就是当前最好的行动方案。
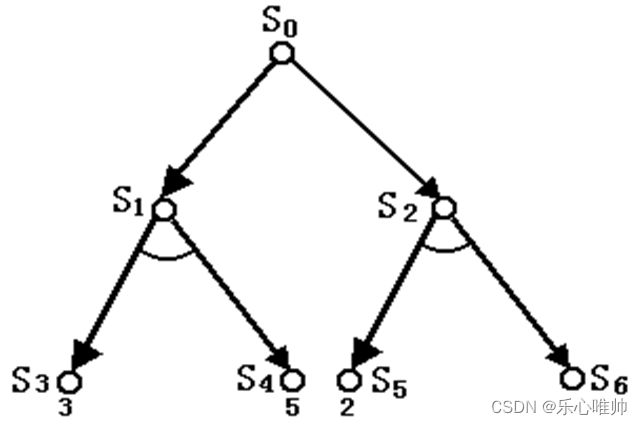
3、a-b剪枝法
例:对于下面的博弈树进行剪枝
十、不确定性知识表示
1、不确定性推理的概念
不确定性推理泛指除精确推理以外的其他各种推理问题。包括不完备、不精确知识的推理、模糊知识推理,非单调性推理等。
(只求概念理解、习题会做就行,涉及比较少、因为难度较大)
可信度推理、bayes推理、概率推理
课后习题也看一看
十一、机器学习
1、决策树
id3算法:(很重要、复杂、信息增益、要记住公式、要亲自动手算一算、不能光看、做习题例题、
2、ID3算法
信息熵的概念
信息熵是对信息源整体不确定性的度量。假设S为样本集,S中所有样本的类别有k种,如y1,y2,…,yk,各种类别样本在S上的概率分布分别为P(y1),P(y2),…,P(yk),则S的信息熵可定义为:
信息增益的概念
3、SVM
(了解概念即可、分类的基本思想:升维、画超平面、)
十二、神经网络
1、人工神经元基本计算方法和公式(很重要)、
2、各种激励函数(了解)
最常用 sigmoid
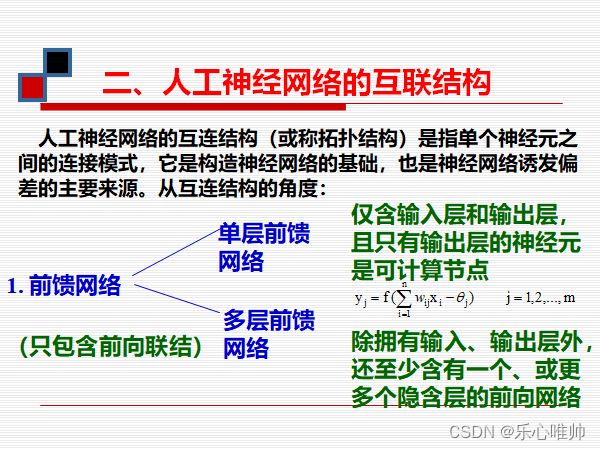
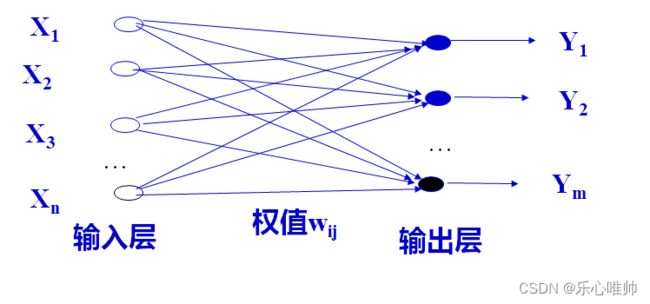
3、前馈问题、反馈模型的基本拓扑结构和它们之间的区别
3、前馈网络的基本拓扑结构
4、反馈网络的基本拓扑结构
5、BP网络模型
双向传播问题:正向传播的作用、逆向传播的作用、两者之间的区别
正向传播:输入信息由输入层传至隐层,最终在输出层输出。
反向传播:修改各层神经元的权值,使误差信号最小。
6、hopfied网络
全连接、反馈网络
7、CNN
1)卷积、卷积核的概念
卷积(convolution)在卷积神经网络中的主要作用是实现卷积操作,形成网络的卷积层。
卷积操作的基本过程是:针对图像的某一类特征,先构造其特征过滤器(FF),然后利用该滤器对图像进行特征提取,得到相应特征的特征图( FM)。依此针对图像的每一类特征,重复如上操作,最后得到由所有特征图构成的卷积层。
特征过滤器也称为卷集核(Coiling Kernel,CK),它实际上是由相关神经元连接权值所形成的一个权值矩阵,该矩阵的大小由卷集核的大小确定。卷集核与特征图之间具有一一对应关系,一个卷集核唯一地确定了一个特征图,而一个特征图也唯一地对应着一个卷积核。
2)池化、池化层的概念
池化层(Pooling Layer)也叫子采样层(Subsample Layer)或降采样(downsampling),其主要作用是利用子采样(或降采样)对输入图像的像素进行合并,得到池化层的特征图谱。
池化操作的一个重要概念是池化窗口或子采样窗口。所谓池化窗口是指池化操作所使用的一个矩形区域,池化操作利用该矩形区域实现对卷积层特征图像素的合并。
例如,一个8*8的输入图像,若采用大小为2*2的池化窗口对其进行池化操作,就意味着原图像上的4个像素将被合并为1个像素,原卷积层中的特征图经池化操作后将缩小为原图的1/4。
池化操作的基本过程是:从特征图的左上角开始,按照池化窗口,先从左到右,然后再从上向下,不重叠地依次扫过整个图像,并同时利用子采样方法进行池化计算。
常用的池化方法有最大池化(max pooling)法、平均池化(mean pooling)法和概率矩阵池化(stochastic pooling)法等。这里主要讨论最大池化法和平均池化法。