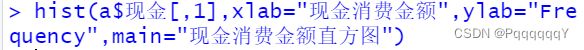R语言的基本统计分析
通过综合案例,使用R语言掌握基本统计分析的各种指标的并掌握统计分析结果的可视化方法。
1.背景介绍
Consolidated食品公司在新墨西哥州、亚利桑那州和加利福尼亚州经营连锁超市。它举办了一个促销活动,宣传本公司新的信用卡政策,以及顾客在购物付款时除了使用现金和个人支票外,还能够使用诸如VISA卡和Mater卡这样的信用卡。新政策正在试验的基础上实行,公司希望信用卡支付方式能够鼓励顾客多消费。
在新政策实行一个月以后,工作人员选择一周时间内的100位顾客作为随机样本,搜集了每位顾客的支付方式和消费金额数据,全部数据在Consolid.csv文件中。
2. 问题讨论
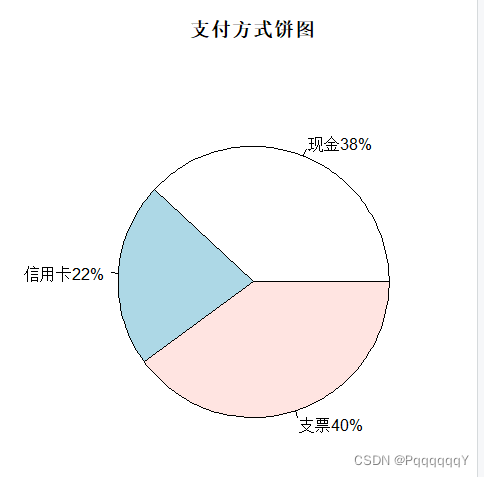
a)计算支付方式的频数和相对频率。画出支付方式的相对频率的饼图。
实验结果如下:
计算支付方式的频率:
计算支付方式的相对频率:
再绘制饼图:
结果如下图所示:
绘图代码如下:
a<-table(data$支付方式)/100
d<-c("现金","信用卡","支票")
b<-paste(d,a*100,"%",sep = "")
pie(a,labels = q,main = "支付方式饼图")b)计算每种支付方式下消费金额的频数和相对频率的分布。画出支付方式的相对频率的饼图。
消费金额的频数:
相对频率:
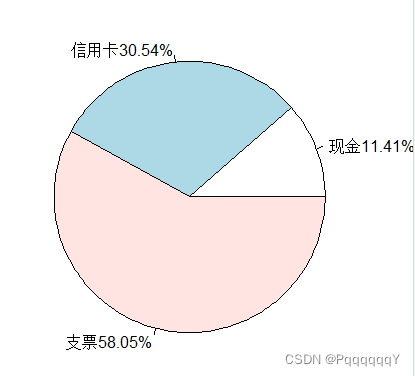
绘制图形如下图所示:
得到下面的图形:
绘图代码如下:
b<-lapply(a,function(a){
apply(a[1], 2, sum)})
l<-round(unlist(b)/sum(unlist(b))*100,2)
la<-paste(d,l,"%",sep="")
pie(unlist(b),labels = la)c)画出每种支付方式下消费金额的直方图。
根据支付方式分类为列表
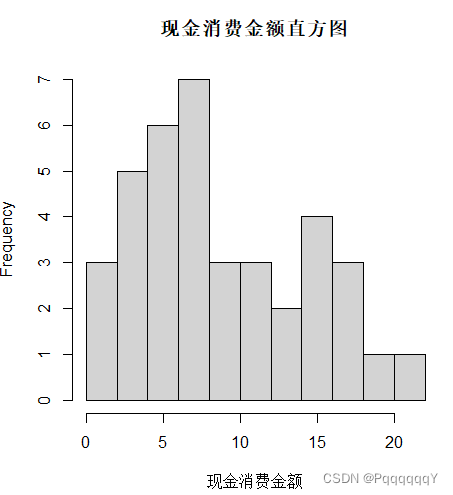
现金消费金额直方图:
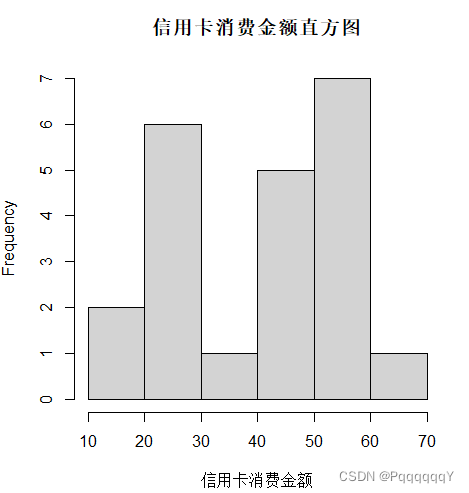
信用卡消费金额直方图:
支票消费金额直方图:
绘图部分的代码如下:
hist(a$现金[,1],xlab="现金消费金额",ylab="Fre
quency",main="现金消费金额直方图")
hist(a$信用卡[,1],xlab="信用卡消费金额",ylab
="Frequency",main="信用卡消费金额直方图")
hist(a$支票[,1],xlab="支票消费金额",ylab="Fre
quency",main="支票消费金额直方图")
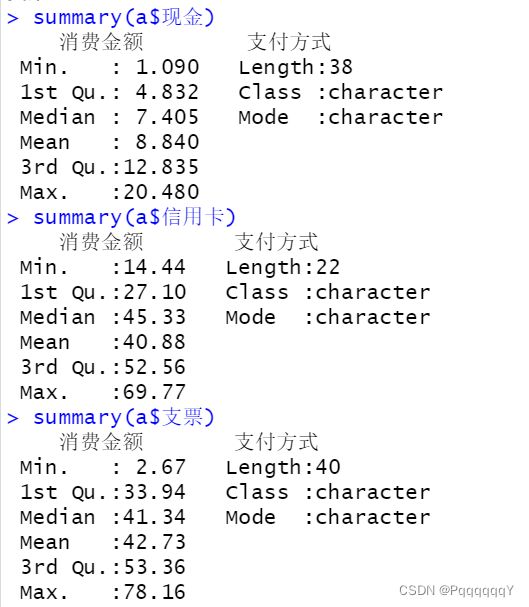
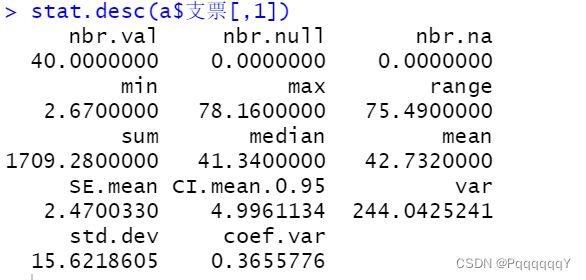
d)计算每种支付方式数据的集中趋势和离散程度。
先用summary函数查看信息
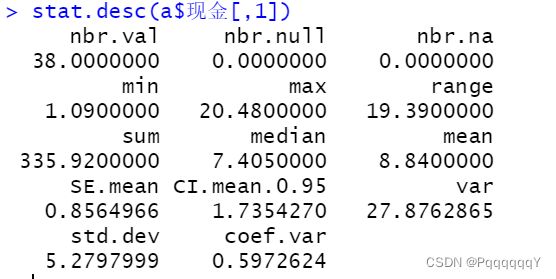
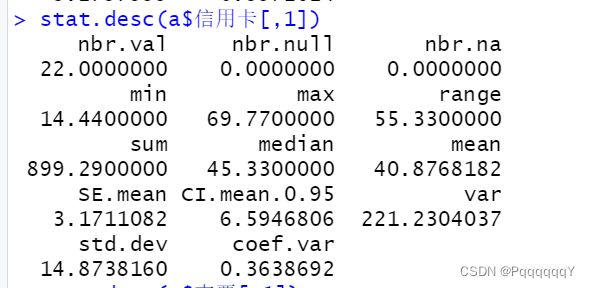
计算极差和标准差,std为标准差,range为极差。
填写表格如下图所示:
| 支付方式 |
平均值 |
最小值 |
下四分位数 |
中位数 |
上四分位数 |
最大值 |
标准差 |
极差 |
四分位差 |
| 现金 |
8.840 |
1.090 |
4.832 |
7.045 |
12.835 |
20.480 |
5.2798 |
19.39 |
8.003 |
| 信用卡 |
40.88 |
14.44 |
27.10 |
45.33 |
52.56 |
69.77 |
14.87382 |
55.33 |
25.46 |
| 支票 |
42.73 |
2.67 |
33.94 |
41.34 |
53.36 |
78.16 |
15.62186 |
75.49 |
19.42 |
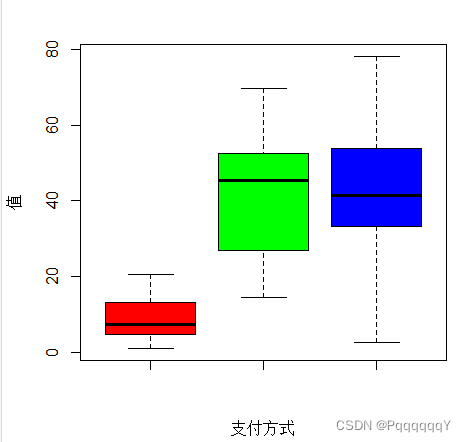
e)画出三种支付方式数据的箱线图。
绘制图形如下图所示:
代码如下:
boxplot(a$现金[,1],a$信用卡[,1],a$支票[,1],yl
ab="值",xlab="支付方式",col=c("red","green","b
lue"))3.基于2,给出数据分析的相应结论。
结论1:支票和现金的使用频率最高且相差不大,信用卡使用则较少,支付金额最高的是支票,其次是信用卡,最低的是现金。
结论2:支票和信用卡的稳定性比较小,现金则比较稳定,差别不大。
综上:可以得出使用支票和信用卡的人数较多,使用现金的人数较少,使用支票和信用卡的消费金额也比使用现金的消费金额多。