深度学习系列:卷积神经网络(CNN)和LeNet 5
前言
前面介绍了全连接神经网络并将其运用在MNIST手写数字的数据集上,能够取得一定的准确率,但是对于图像的识别,我们有一种更高效、更准确的神经网络模型:卷积神经网络(Convolutional Neural Network)。这种网络相较于全连接神经网络而言,更能够体现出图像像素相对位置的影响,而且需要训练的参数更小,对于全连接神经网络而言,网络层数增多之后训练起来难度很大,且伴随着梯度消失问题,卷积神经网络也一定程度上解决了这种问题。
ReLU激活函数
首先介绍一种新的激活函数类型:ReLU函数,之前网络使用的是Sigmoid函数,我们对比一下两种激活函数。

ReLU函数的表达式为:
f ( x ) = { x x > 0 0 x ≤ 0 f(x)=\left\{ \begin{aligned} x & & x>0 \\ 0 & & x \le0 \\ \end{aligned} \right. f(x)={x0x>0x≤0
也可以直接表示为对 0 0 0和 x x x求最大值。这个ReLU函数是2012年Alex在AlexNet中使用的,也是现在广泛使用的激活函数。ReLU函数有几个特点:
1.能够避免BP网络训练过程中的梯度消失问题,从上篇文章的梯度推导可以直到,反向传播时每传播一层就会乘以一个激活函数的导数,对于Sigmoid函数而言,它导数的最大值为 0.25 0.25 0.25,神经网络的层数一多就会使得梯度越来越小,直至出现“梯度消失”问题。ReLU函数在正半轴的导数始终为1,不存在该问题。
2.计算量更小,相较于Sigmoid函数的指数计算,ReLU函数只是求最大值的过程。
3. 具有稀疏性,ReLU函数在小于0时值为0,减小过拟合的概率,当然也有可能导致某些神经元输出永远都是0,产生神经元死去的现象。
卷积神经网络
网络结构
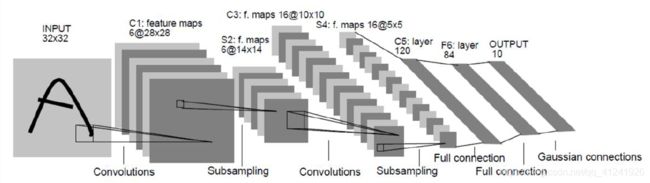
卷积神经网络的构造如上如所示,它由若干个卷积层、池化层和全连接层组成。上图中,首先对输入的 32 × 32 32\times32 32×32图像进行卷积操作(后面会详细解释)得到6个尺寸为 28 × 28 28\times28 28×28的feature map,然后进行下采样也就是池化操作得到6张 14 × 14 14\times14 14×14的map,之后再进行卷积操作得到16张 10 × 10 10\times10 10×10的map,然后是池化得到16张 5 × 5 5\times5 5×5的map,最后就是我们之前讲过的全连接层将 16 × 5 × 5 16\times5\times5 16×5×5经过几个全连接层分至10类。
我们可以看到卷积神经网络的结构为:
输入图像 → \to →若干卷积层 → \to →一个池化层 → \to →若干卷积层 → \to →一个池化层 → . . . . . . → \to ......\to →......→全连接层
接下来介绍卷积和池化如何操作。
卷积操作(Conv)
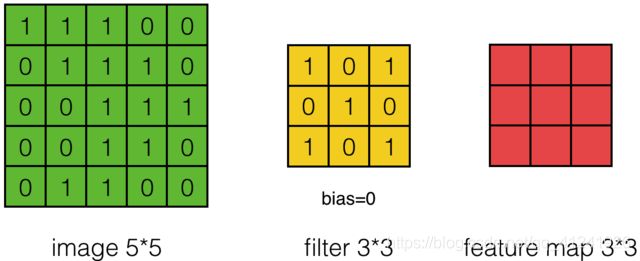
这里举例说明卷积操作,这里用一个 3 × 3 3\times3 3×3的 卷积核(filter) 对 5 × 5 5\times5 5×5的图像进行卷积,这个过程通俗的来讲就是将卷积核游走在被卷积的图像上,对应位置相乘求和得到最后的feature map。
注:下列动图均非本人制作,从百度图片中获取
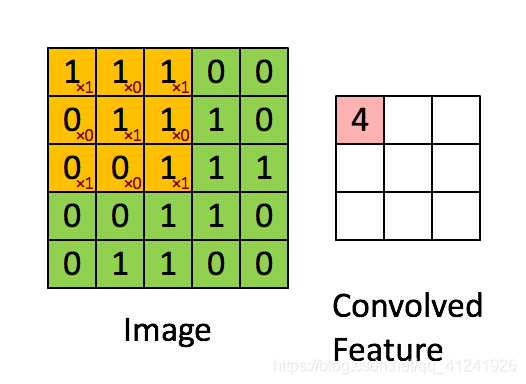
比如对feature中的第一个元素计算过程如下图,卷积核元素和图像元素对应乘积再求和:
1 × 1 + 1 × 0 + 1 × 1 + 0 × 0 + 1 × 1 + 1 × 0 + 0 × 1 + 0 × 0 + 1 × 1 = 4 1\times1+1\times0+1\times1+0\times0+1\times1+1\times0+0\times1+0\times0+1\times1=4 1×1+1×0+1×1+0×0+1×1+1×0+0×1+0×0+1×1=4
整个卷积过程可用下图表示:
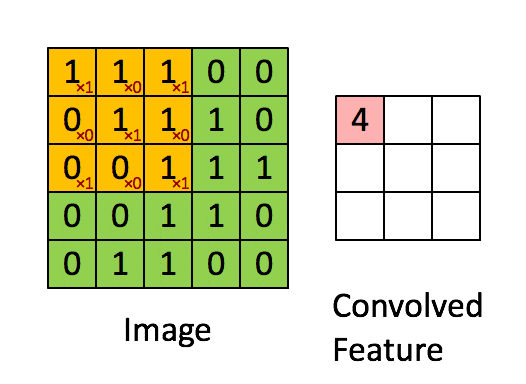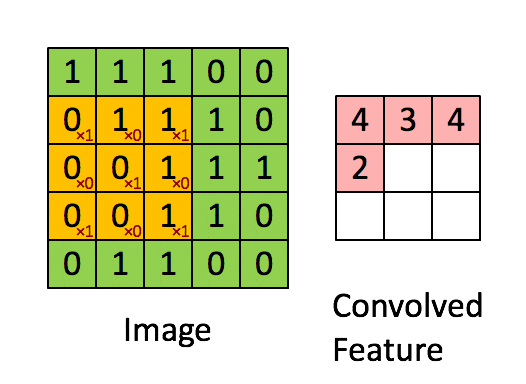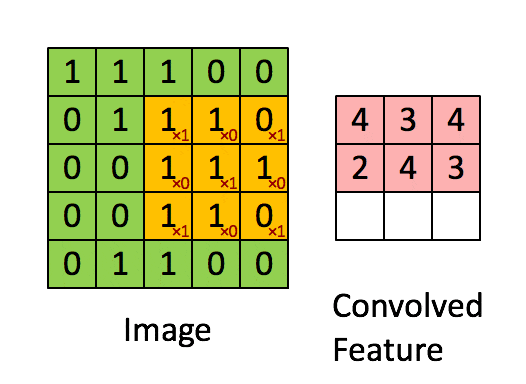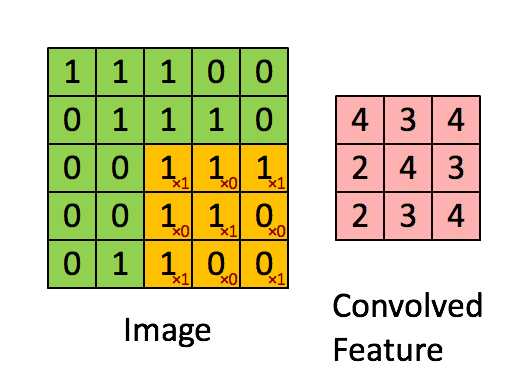
上面演示的就是最简单的卷积操作,卷积有几个重要的参数:
卷积核大小:F,就是filter的宽度。
步幅Stride:S,步幅至卷积核一次游走的像素间隔,上面演示的卷积步幅为1。
补零Zero Padding:Z,Padding就是指在卷积之前对图像四周进行补零的圈数。从上面的卷积过程可以看到,我们从 5 × 5 5\times5 5×5的图像卷积后得到了 3 × 3 3\times3 3×3的图像,有时候我们希望图像不减小,那么可以通过事先在原图像上进行四周补零实现。
这里还有一个十分重要的公式,就是卷积前后图像大小关系,假设卷积前图像宽度 W 1 W_1 W1,卷积后的feature map宽度为 W 2 W_2 W2,它们的关系用下式表示:
W 2 = [ ( W 1 − F + 2 × Z ) / S ] + 1 W_2 = [(W_1 - F + 2\times Z)/S ]+ 1 W2=[(W1−F+2×Z)/S]+1
上面的中括号为向下取整操作。
对于一开始提到的卷积神经网络中,第一次卷积得到了6张feature map,这其实就是在一张图像中用多个不同的卷积核进行卷积形成的,不同的卷积核对应不同的通道,也就是说我们通过不同的卷积核得到不同的map。
接下来的问题就是如何对多通道的图像进行卷积呢?或者说上面6通道的feature map如何进行卷积呢?其实很简单,我们只要每个通道对应一个卷积核就行了,具体过程用下图表示:
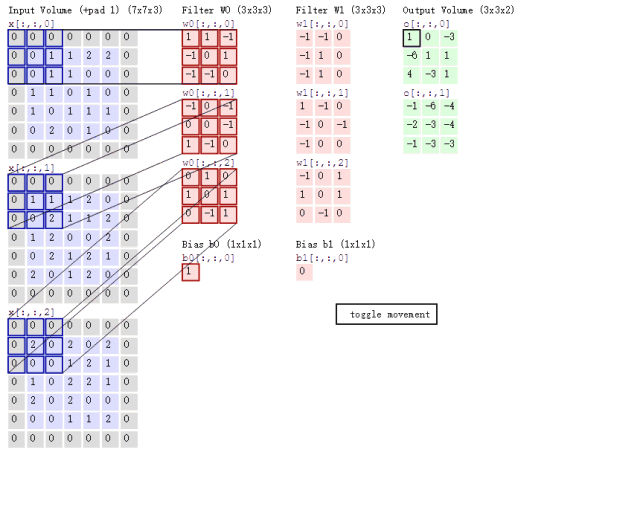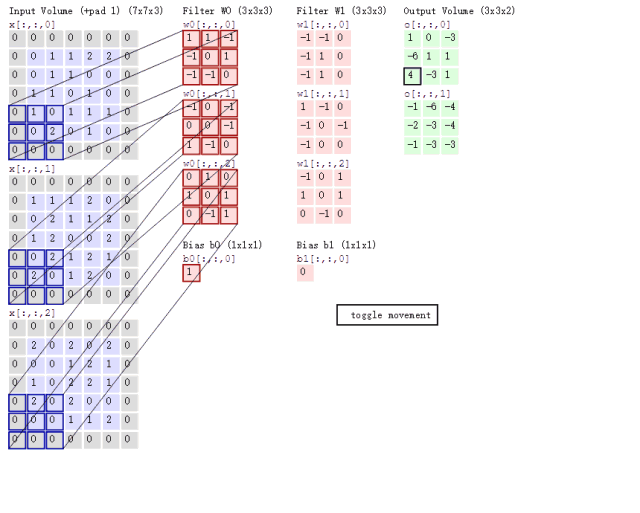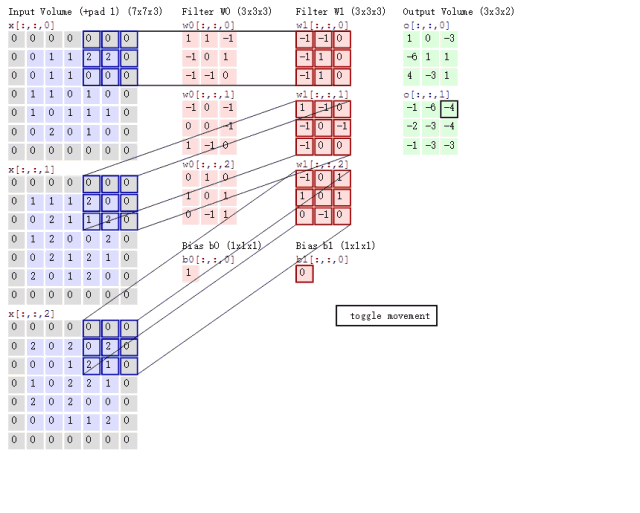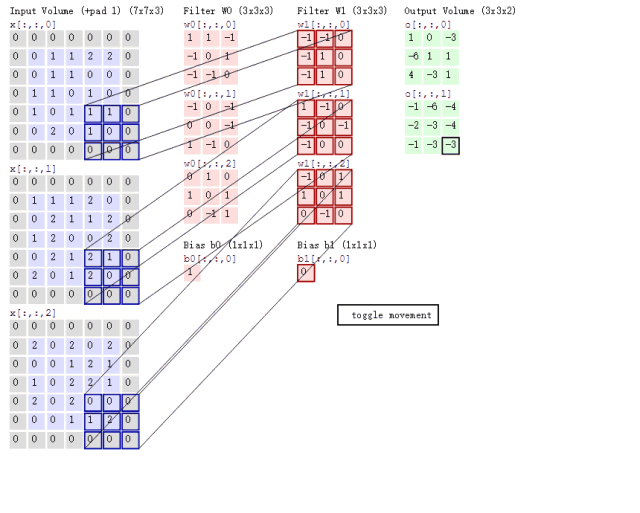
这里对一张3通道的图像进行卷积,那么我们的卷积核必须也是三通道的,也就是 3 × 3 × 3 3\times 3\times 3 3×3×3的卷积核卷积后能得到一张新的map,上图中用了两个 3 × 3 × 3 3\times 3\times 3 3×3×3的核得到了2张map。
池化操作(Pooling)
池化操作是一个下采样的过程。可以进一步的减小feature map的大小从而减小参数的数量。Pooling的方法有很多,常见的类型有最大值池化(Max Pooling)和均值池化(Average Pooling),最大值池化的过程见下图:
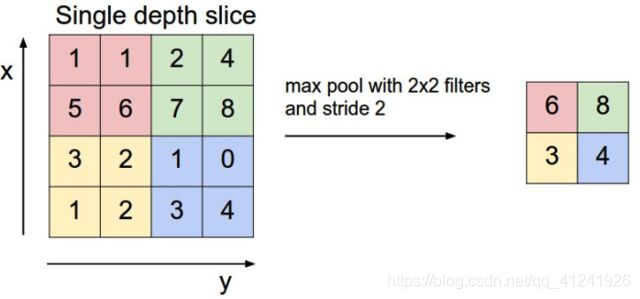
Pooling操作同样有和卷积操作一样的三个参数:filter,stride和padding,Pooling操作前后的图像大小关系也和卷积一致。 也就是满足下面关系:
W 2 = [ ( W 1 − F + 2 × Z ) / S ] + 1 W_2 = [(W_1 - F + 2\times Z)/S ]+ 1 W2=[(W1−F+2×Z)/S]+1
中括号为向下取整。
卷积神经网络LeNet 5
LeNet 5是Yann LeCun教授在1998年提出的一种卷积神经网络,被用于手写数字的识别,准确率达到了99.2%,这个网络也具备了当今卷积神经网络的全部要素。网络结构图开篇已经给出:

结构为:
| type | patch size/stride | output size |
|---|---|---|
| Conv | 5 × 5 / 1 5\times 5 / 1 5×5/1 | 6 × 28 × 28 6\times 28\times 28 6×28×28 |
| Pooling | 2 × 2 / 1 2\times 2 / 1 2×2/1 | 6 × 14 × 14 6\times 14\times 14 6×14×14 |
| Conv | 5 × 5 / 1 5\times 5 / 1 5×5/1 | 16 × 10 × 10 16\times 10\times 10 16×10×10 |
| Pooling | 2 × 2 / 1 2\times 2 / 1 2×2/1 | 16 × 5 × 5 16\times 5\times 5 16×5×5 |
| FC | ------ | 120 120 120 |
| FC | ------ | 84 84 84 |
| FC | ------ | 10 10 10 |
可以看到一共是7层结构,网络比较简单,接下来我们通过pytorch编写一个LeNet 5对MNIST手写数字进行分类,看看它的表现到底怎么样。
LeNet 5 实现
这里有两点说明:
- LeNet 5输入的图像为 32 × 32 32\times 32 32×32,Mnist数据集的图像大小为 28 × 28 28\times28 28×28,可以将图像resize,torchvision.transform就有resize的变换方法;我这里是直接将第二个卷积操作的卷积核改为 3 × 3 3\times3 3×3,这样就能够匹配。(目前的示例都是直接使用torch的数据集,这里推荐大家也可以自己编写Dataset类,torch的官方教程有介绍)
- LeNet 5的激活函数采取的仍然是Sigmoid函数,ReLU是Alex在2012年的AlexNet中提出并使用的,这里我直接使用ReLU函数,因为这个激活函数效果更好,也更常用。
这里给出网络搭建的代码,实际上和上一篇文章的FC网络代码有大部分重复的(实际上也是copy过来的),改过的地方就是网络的结构,多了卷积层和池化层。
import torch
import torch.nn as nn
import torch.nn.functional as f
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# 优先选择gpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# LeNet 5用于对Mnist数据集分类
class CnnNet(nn.Module):
def __init__(self):
super(CnnNet, self).__init__()
# 5*5卷积核卷积
self.conv1 = nn.Conv2d(1, 6, (5, 5))
# 3*3卷积核卷积(为了输入28*28能够匹配,原网络是5*5卷积核)
self.conv2 = nn.Conv2d(6, 16, 3) # 卷积核为方阵的时候可以只传入一个参数
self.pool = nn.MaxPool2d((2, 2))
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
"""
前向传播函数,返回为一个size为[batch_size,features]的向量
:param x:
:return:
"""
# 卷积+relu+池化
x = self.pool(f.relu(self.conv1(x)))
x = self.pool(f.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = f.relu(self.fc1(x))
x = f.relu(self.fc2(x))
x = self.fc3(x)
return x
# 训练网络
def train(train_loader):
# 损失函数值
running_loss = 0.0
for i, data in enumerate(train_loader, 0):
inputs, labels = data
# 如果有gpu,则使用gpu
inputs, labels = inputs.to(device), labels.to(device)
# 梯度置零
optimizer.zero_grad()
# 前向传播
output = net(inputs)
# 损失函数
loss = criterion(output, labels)
# 反向传播,权值更新
loss.backward()
optimizer.step()
running_loss += loss.item()
# 每50个batch_size后打印一次损失函数值
if i % 100 == 99:
print('%5d loss: %.3f' %
(i + 1, running_loss / 100))
running_loss = 0.0
# 训练完1个或几个epoch之后,在测试集上测试以下准确率,防止过拟合
def test(test_loader):
correct = 0
total = 0
# 不进行autograd
with torch.no_grad():
for data in test_loader:
images, labels = data
images, labels = images.to(device), labels.to(device)
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on test images: %d %%' % (
100 * correct / total))
return correct / total
if __name__ == '__main__':
# Pytorch自带Mnist数据集,可以直接下载,分为测试集和训练集
train_dataset = datasets.MNIST(root='./data/', train=True, transform=transforms.ToTensor(), download=True)
test_dataset = datasets.MNIST(root='./data/', train=False, transform=transforms.ToTensor(), download=True)
# DataLoader类可以实现数据集的分批和打乱等
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=False)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)
net = CnnNet().to(device)
# 准则函数使用交叉熵函数,可以尝试其他
criterion = nn.CrossEntropyLoss()
# 优化方法为带动量的随机梯度下降
optimizer = torch.optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(20):
print('Start training: epoch {}'.format(epoch+1))
train(train_loader)
test(test_loader)
代码比较简单,就不过多说明,代码也有部分注释。网络的结构比较简单,训练起来也比较快,如果电脑有NVIDIA的显卡的话训练更快。给出我电脑上训练的结果:
训练完第8轮之后,测试集上的准确率达到了0.98,参数只是粗略的给了以下,可以尝试修改优化的损失函数以及优化方法进行训练。不管怎么说,这已经是一个非常好的成绩了,相比全连接网络而言更优秀。
总结
这篇文章主要介绍了卷积神经网络的一般结构,重点介绍了卷积操作(Conv)和池化操作(Pooling)的具体运算,最后简单介绍了LeNet 5网络并用它对Mnist数据集进行了分类。
本文源代码链接:https://github.com/Fanxiaodon/nn/tree/master/CNNMnist
当然本文只是对卷积神经网络有个大概的介绍,便于快速上手和运用CNN进行分类,对于反向传播的训练细节没有进行推导,想了解可以查找其它资料。
LeNet 5 只是最早的一批卷积神经网络,从网络的层数和结构来看,还算不上深度网络,近年来卷积神经网络提出一些新型的大规模网络,例如AlexNet、VGGNet、GoogLeNet以及ResNet等,层数更深、效果也更好,后面的文章将介绍这些网络的结构,以及将它们运用在不同的数据集进行代码演示。