最大流与最小割(Maxflow与Mincut)
传统图像主要分割算法:
基于阈值的分割
(1)固定阈值分割
(2)直方图双峰法
(3)迭代阈值图像分割
(4)自适应阈值图像分割
(5)最佳阈值法
2.基于边缘的分割
(1)Canny边缘检测器
(2)Harris角点检测器
(3)Sift检测器
(4)Surf检测器
3.基于区域的分割
(1)种子区域生长法
(2)区域分裂合并法
(3)分水岭法
4.基于图论的分割
(1)GraphCut图割
(2)GrabCut分割和抠图
5.基于能量泛函的分割
(1)参数主动轮廓模型
(2)ASM
(3)AAM
(4)CLM
(5)GAC
该文章讲述的最大流与最小割实际上就是图论分割的主要思想。将图像映射为带权无向图,把像素视作节点,将图像分割问题看作是图的顶点划分问题,利用最小剪切准则得到图像的最佳分割。
最大流算法
最大流算法就像水管水流,如何保证S点到T点的水流量最大。其中点与点之间的表示水管最大容量。
最大流解法有很多,例如Ford-Fulkerson算法,Edmond-Karp 算法,Dinic算法等。
Ford-Fulkerson算法
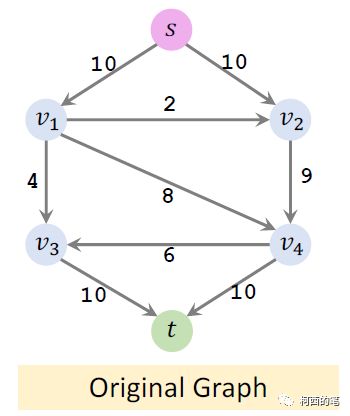
原始图
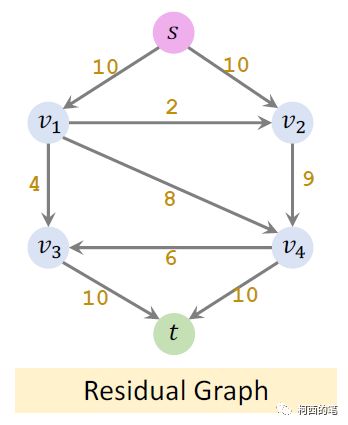
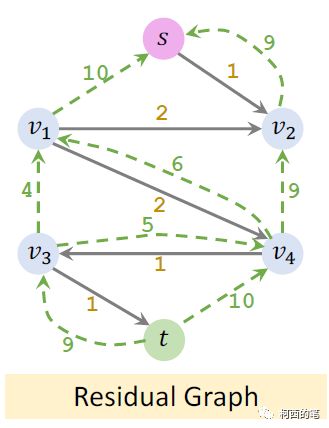
剩余流量图
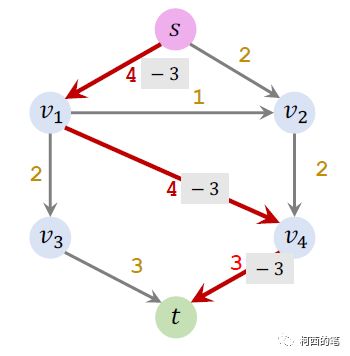
在剩余流量图中随便找一条从s到t的路线
减去最小容量
然后构建反向箭头
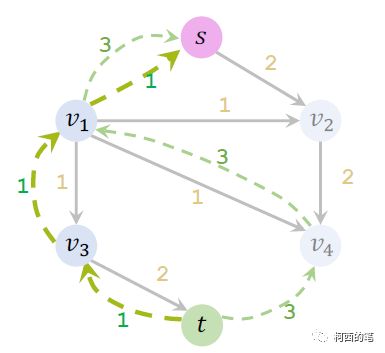
接着再找一条从s到t的路线,重复上面的计算
继续找新路线
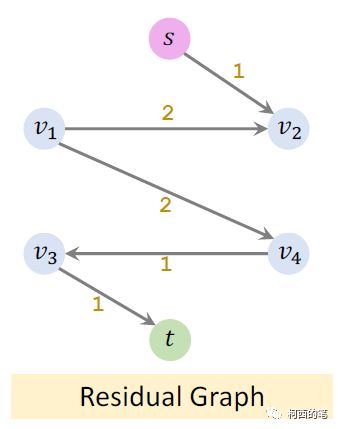
此时已经找不到新的路径从s到t,结束进程。
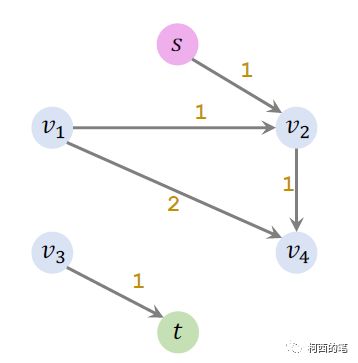
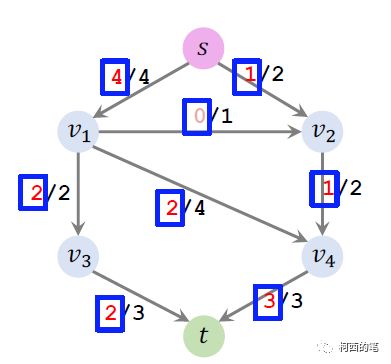
再利用公式flow = capacity - residual
既可以得出最大流5。
代码实现:
class Edge():
''' 流网络中的边 '''
def __init__(self, v, w, cap, flow=0):
'''
定义一条边 v→w
:param v: 起点
:param w: 终点
:param cap: 容量
:param flow: v→w上的流量
'''
self.v, self.w, self.cap, self.flow = v, w, cap, flow
def other_node(self, p):
''' 返回边中与p相对的另一顶点 '''
return self.v if p == self.w else self.w
def residual_cap_to(self, p):
'''
计算残存边的剩余容量
如果p=w,residual_cap_to(p)返回 v→w 的剩余容量
如果p=v,residual_cap_to(p)返回 w→v 的剩余容量
'''
return self.cap - self.flow if p == self.w else self.flow
def moddify_flow(self, p, x):
''' 将边的流量调整x '''
if p == self.w: # 如果 p=w,将v→w的流量增加x
self.flow += x
else: # 否则将v→w的流量减少x
self.flow -= x
def __str__(self):
return str(self.v) + '→' + str(self.w)
class Network():
''' 流网络 '''
def __init__(self, E: list, s: int, t: int):
'''
:param E: 边集
:param s: 原点
:param t: 汇点
:return:
'''
self.E, self.s, self.t = E, s, t
def edges_from(self, v):
''' 从v顶点流出的边 '''
return [edge for edge in self.E if edge.v == v]
def edges_to(self, v):
''' 流入v顶点的边 '''
return [edge for edge in self.E if edge.w == v]
def edges(self, v):
''' 连接v顶点的所有边 '''
return self.edges_from(v) + self.edges_to(v)
def flows_from(self, v):
'''v顶点的流出量 '''
edges = self.edges_from(v)
return sum([e.flow for e in edges])
def flows_to(self, v):
''' v顶点的流入量 '''
edges = self.edges_to(v)
return sum([e.flow for e in edges])
def check(self):
''' 源点的流出是否等于汇点的流入 '''
return self.flows_from(self.s) == self.flows_to(self.t)
def display(self):
if self.check() is False:
print('该网络不符合守恒定律')
return
print('%-10s%-8s%-8s' % ('边', '容量', '流'))
for e in self.E:
print('%-10s%-10d%-8s' %
(e, e.cap, e.flow if e.flow < e.cap else str(e.flow) + '*'))
class FordFulkerson():
def __init__(self, G: Network):
self.G = G
self.max_flow = 0 # 最大流
class Node:
''' 用于记录路径的轨迹 '''
def __init__(self, w, e: Edge, parent):
'''
:param w: 顶点
:param e: 从上一顶点流入w的边
:param parent: 上一顶点
'''
self.w, self.e, self.parent = w, e, parent
def dfs(self):
''' 获取网络中的一条增广路径 '''
path = None
visited = set() # 被访问过的顶点
visited.add(self.G.s)
q = []
q.append(self.Node(self.G.s, None, self.G.t))
tempmaxflow = 1e10
while len(q):
node_v = q.pop(0)
v = node_v.w
label = 0
for e in self.G.edges(v): # 遍历连接v的所有边
w = e.other_node(v) # 边的另一顶点,e的指向是v→w
# v→w有剩余容量且w没有被访问过
if e.residual_cap_to(w) > 0 and w not in visited:
visited.add(w)
node_w = self.Node(w, e, node_v)
q.append(node_w)
if w == self.G.t: # 到达了汇点
path = node_w
label = 1
break
if label == 1: # 到达了汇点
break
if path is None:
tempmaxflow = 0
return tempmaxflow
node = path
while node.parent != self.G.t: # 计算增广路径上的最小剩余量
w, e = node.w, node.e
tempmaxflow = min(tempmaxflow, e.residual_cap_to(w))
node = node.parent
node = path
while node.parent != self.G.t: # 修改残存网
w, e = node.w, node.e
e.moddify_flow(w, tempmaxflow)
node = node.parent
return tempmaxflow
def start(self):
''' 增广路径最大流算法主体方法 '''
while True:
tempmaxflow = self.dfs() # 找到一条增广路径
if tempmaxflow ==0:
break
self.max_flow += tempmaxflow # 扩充最大流
def display(self):
print('最大网络流 = ', self.max_flow)
print('%-10s%-8s%-8s' % ('边', '容量', '流'))
for e in self.G.E:
print('%-10s%-10d%-8s' %
(e, e.cap, e.flow if e.flow < e.cap else str(e.flow) + '*'))
E = [Edge(1, 2, 4), Edge(1, 3, 2), Edge(2, 4, 2), Edge(2, 5, 4),
Edge(2, 3, 1), Edge(3, 5, 2), Edge(4, 6, 3), Edge(5, 6, 3)]
s, t = 1, 6
G = Network(E, s, t)
ford_fullkerson = FordFulkerson(G)
ford_fullkerson.start()
ford_fullkerson.display()Ford-Fulkerson算法的时间复杂度较高,接下来讲述一种使用较为广泛,时间复杂度低的Dinic算法。
Dinic算法
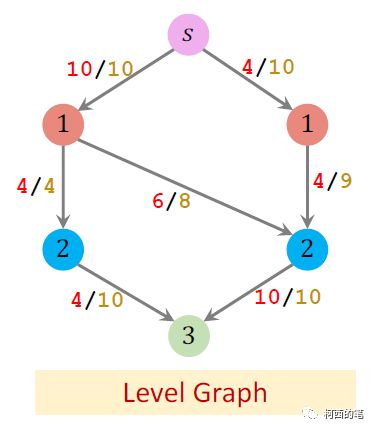
Dinic算法首先根据剩余流量图建立一个Level Graph,如下:
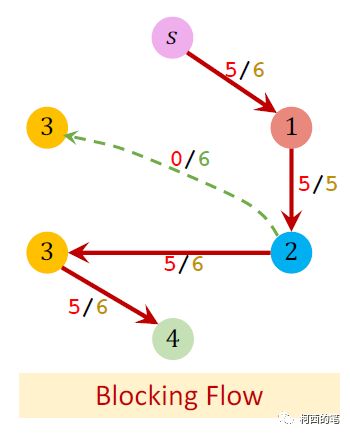
然后在level graph上寻找阻塞流,再将其映射回原先的residual graph中。
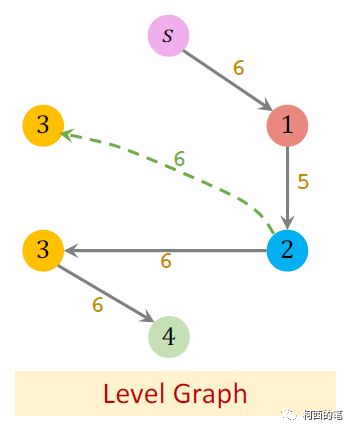
然后在新的residual graph中再次建立level graph图。
再寻找阻塞流,然后再映射回residual graph。如此不断循环,直到在新生成的level graph中找不到从s到t的阻塞流。
再利用公式flow = capacity - residual
最大流量为19。
代码实现
class Edge():
''' 流网络中的边 '''
def __init__(self, v, w, cap, flow=0):
'''
定义一条边 v→w
:param v: 起点
:param w: 终点
:param cap: 容量
:param flow: v→w上的流量
'''
self.v, self.w, self.cap, self.flow = v, w, cap, flow
def other_node(self, p):
''' 返回边中与p相对的另一顶点 '''
return self.v if p == self.w else self.w
def residual_cap_to(self, p):
'''
计算残存边的剩余容量
如果p=w,residual_cap_to(p)返回 v→w 的剩余容量
如果p=v,residual_cap_to(p)返回 w→v 的剩余容量
'''
return self.cap - self.flow if p == self.w else self.flow
def moddify_flow(self, p, x):
''' 将边的流量调整x '''
if p == self.w: # 如果 p=w,将v→w的流量增加x
self.flow += x
else: # 否则将v→w的流量减少x
self.flow -= x
def __str__(self):
return str(self.v) + '→' + str(self.w)
class Network():
''' 流网络 '''
def __init__(self, E: list, s: int, t: int):
'''
:param E: 边集
:param s: 原点
:param t: 汇点
:return:
'''
self.E, self.s, self.t = E, s, t
def edges_from(self, v):
''' 从v顶点流出的边 '''
return [edge for edge in self.E if edge.v == v]
def edges_to(self, v):
''' 流入v顶点的边 '''
return [edge for edge in self.E if edge.w == v]
def edges(self, v):
''' 连接v顶点的所有边 '''
return self.edges_from(v) + self.edges_to(v)
def flows_from(self, v):
'''v顶点的流出量 '''
edges = self.edges_from(v)
return sum([e.flow for e in edges])
def flows_to(self, v):
''' v顶点的流入量 '''
edges = self.edges_to(v)
return sum([e.flow for e in edges])
def check(self):
''' 源点的流出是否等于汇点的流入 '''
return self.flows_from(self.s) == self.flows_to(self.t)
def display(self):
if self.check() is False:
print('该网络不符合守恒定律')
return
print('%-10s%-8s%-8s' % ('边', '容量', '流'))
for e in self.E:
print('%-10s%-10d%-8s' %
(e, e.cap, e.flow if e.flow < e.cap else str(e.flow) + '*'))
class FordFulkerson():
def __init__(self, G: Network):
self.G = G
self.max_flow = 0 # 最大流
class Node:
''' 用于记录路径的轨迹 '''
def __init__(self, w, e: Edge, parent):
'''
:param w: 顶点
:param e: 从上一顶点流入w的边
:param parent: 上一顶点
'''
self.w, self.e, self.parent = w, e, parent
def bfs(self):
visited = {self.G.s}
tempvisited = {self.G.s}
q = []
q.append(self.Node(self.G.s, None, self.G.t))
q.append("end")
NewE = []
label = 0
while len(q)>1:
node_v = q.pop(0)
if node_v=="end":
q.append("end")
visited = tempvisited.copy()
continue
v = node_v.w
for e in self.G.edges(v): # 遍历连接v的所有边
w = e.other_node(v) # 边的另一顶点,e的指向是v→w
if e.residual_cap_to(w) > 0 and w not in visited and e not in NewE:
tempvisited.add(w)
node_w = self.Node(w, e, node_v)
q.append(node_w)
NewE.append(e)
if w == self.G.t: # 到达了汇点
label = 1
return Network(NewE,self.G.s,self.G.t),label
def dfs(self,NewNetwork):
''' 获取网络中的一条增广路径 '''
path = None
path2 = None
visited = set() # 被访问过的顶点
visited.add(self.G.s)
q = []
q.append(self.Node(self.G.s, None, self.G.t))
q2 = []
q2.append(self.Node(self.G.s, None, self.G.t))
tempmaxflow = 1e10
while len(q):
node_v = q.pop(0)
node_v2 = q2.pop(0)
v = node_v.w
label = 0
for e in NewNetwork.edges(v): # 遍历连接v的所有边
w = e.other_node(v) # 边的另一顶点,e的指向是v→w
e2 = [edge for edge in self.G.E if edge==e][0]
# v→w有剩余容量且w没有被访问过
if e.residual_cap_to(w) > 0 and w not in visited:
visited.add(w)
node_w = self.Node(w, e, node_v)
q.append(node_w)
node_w2 = self.Node(w, e2, node_v2)
q2.append(node_w2)
if w == self.G.t: # 到达了汇点
path = node_w
path2 = node_w2
label = 1
break
if label == 1: # 到达了汇点
break
if path is None:
tempmaxflow = 0
return tempmaxflow
node = path
while node.parent != self.G.t: # 计算增广路径上的最小剩余量
w, e = node.w, node.e
tempmaxflow = min(tempmaxflow, e.residual_cap_to(w))
node = node.parent
node = path2
while node.parent != self.G.t: # 修改残存网
w, e = node.w, node.e
e.moddify_flow(w, tempmaxflow)
node = node.parent
return tempmaxflow
def start(self):
while True:
newnet,label = self.bfs()
if label==0:
break
while True:
tempmaxflow = self.dfs(newnet) # 找到一条增广路径
if tempmaxflow == 0:
break
self.max_flow += tempmaxflow # 扩充最大流
def display(self):
print('最大网络流 = ', self.max_flow)
print('%-10s%-8s%-8s' % ('边', '容量', '流'))
for e in self.G.E:
print('%-10s%-10d%-8s' %
(e, e.cap, e.flow if e.flow < e.cap else str(e.flow) + '*'))
E = [Edge(1, 2, 10), Edge(1, 3, 10), Edge(2, 4, 4), Edge(2, 5, 8),
Edge(2, 3, 2), Edge(3, 5, 9), Edge(4, 6, 10), Edge(5, 6, 10),Edge(5, 4, 6)]
s, t = 1, 6
G = Network(E, s, t)
ford_fullkerson = FordFulkerson(G)
ford_fullkerson.start()
ford_fullkerson.display()最小割算法
最小割实际上就是使用的最大流的计算结果。
最大流与最小割之间转化:将最大流的剩余容量图画出来,然后重起点s出发,将可以连在一块的设为s,另一边即为t
总结:
最大流与最小割是图论分割的基础。接下来我们将继续探讨最大流与最小割如何在图像上实现分割。例如graph cut等。
参考文献:
https://www.its203.com/article/qq_35885429/107226535
https://github.com/wangshusen/AdvancedAlgorithms