NLP 论文领读｜改善意图识别的语义表示：有监督预训练中的各向同性正则化方法

欢迎关注「澜舟 NLP 论文领读」专栏，一起探索前沿技术！ 官网：https://langboat.com

本期分享者：甘子发

澜舟科技算法实习生 郑州大学自然语言处理实验室（ZZUNLP）二年级硕士生，

目前正在进行文本纠错方向的研究。

E-mail: [email protected]

写在前面

意图识别（intent detection）是面向任务对话系统的核心模块，其标注数据较少，所以研究怎样用少量数据训练出一个优秀的意图分类器（few-shot intent detection）有着很高的实用价值。

近年来 BERT 等预训练语言模型（pre-trained language model，PLM）在各 NLP 任务中处于支配地位，而研究表明，在将PLM应用到任务上之前，用相关任务的标注数据先对 PLM 进行有监督的预训练（supervised pre-training，其实就是fine-tuning），可以有效地提升后续微调的效果。对于意图识别，先用少量的公开的对话标注数据对 PLM 进行微调（IntentBERT）[1]，对模型有很大的提升。

但是，IntentBERT 有很强的各向异性（anisotropy），各向异性是一个几何性质，在向量空间上的含义就是分布与方向有关系，语义向量挤在了一个狭窄的锥形空间内，这样向量彼此的余弦相似度都很高，并不是很好的表示，而各向同性（isotropy）就是各个方向都一样，分布均匀。各向异性被认为是导致 PLM 在各下游任务中只能达到次优性能（表示退化问题）的一个重要因素，不过各向同性技术可以用来调整嵌入向量空间，而且使模型在众多任务上的性能都获得了极大的提升。之前的各向同性技术，有些对没经过微调的 PLM（off-the-shelf PLM）进行调整，但对于微调过的 PLM（fine-tuned PLM），这些技术对模型性能反而可能会有负面效果[2]；有的在监督训练过程中进行 isotropic batch normalization，但需要大量训练数据[3]，不适合缺少数据的意图识别任务。

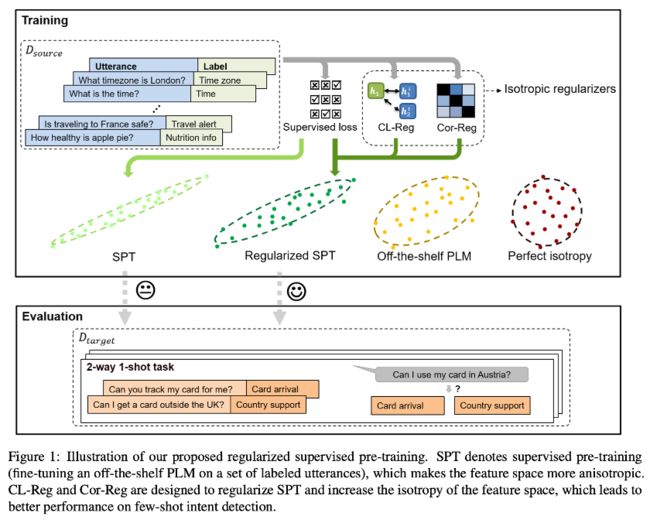
近日有一篇论文《Fine-tuning Pre-trained Language Models for Few-shot Intent Detection: Supervised Pre-training and Isotropization》，其中提出使用各向同性技术来改善 few-shot intent detection的supervised pre-training，在这篇工作中，作者先是研究了 isotropization和supervised pre-training (fine-tuning)之间的关系，然后提出了两种简单有效的各向同性正则化方法（isotropization regularizer），如图 1 所示，并且取得了不错的效果，下面我们一起来看看这篇论文的具体做法吧。

论文标题

Fine-tuning Pre-trained Language Models for Few-shot Intent Detection: Supervised Pre-training and Isotropization

论文作者

Haode Zhang, Haowen Liang, Yuwei Zhang, Liming Zhan, Xiao-Ming Wu, Xiaolei Lu, Albert Y.S. Lam

作者单位

Department of Computing, The Hong Kong Polytechnic University, Hong Kong S.A.R.

University of California, San Diego

Nanyang Technological University, Singapore

Fano Labs, Hong Kong S.A.R.

论文链接

https://arxiv.org/abs/2205.07208

项目代码

https://github.com/fanolabs/isoIntentBert-main

Pilot Study

作者先是做了一些初步实验，以了解各向同性与微调 PLM 之间的相互作用。

论文中使用下列公式计算各向同性：

$\mathrm{I}(\mathbf{V})=\frac{{\min }_{\mathbf{c}\in C}\mathbf{Z}(\mathbf{c},\mathbf{V})}{{\max }_{\mathbf{c}\in C}\mathbf{Z}(\mathbf{c},\mathbf{V})}$ (1)

$\mathbf{Z}(\mathbf{c},\mathbf{V})={\sum }_{i=1}^N\exp \left({\mathbf{c}}^{\top }{\mathbf{v}}_i\right)$ (2)

其中$\mathbf{V}\in {\mathbb{R}}^{N\times d}$是有 zero mean 的 N 个嵌入向量，$C={\mathbf{V}}^{\top }\mathbf{V}$，${\mathbf{v}}_i$是$\mathbf{V}$的第$i$行，$\mathrm{I}(\mathbf{V})\in [0,1]$，值为 1 表示有最高的各向同性。

论文中对比了 PLM 微调前后的各向同性，结果如表 1 所示，可以看到 PLM 经微调后，其各向同性有所下降，即微调可能导致特征空间变得更加各向异性。

然后论文对比了将之前的两种各向同性技术：

• dropout-based contrastive learning [4]
• whitening transformation [5]

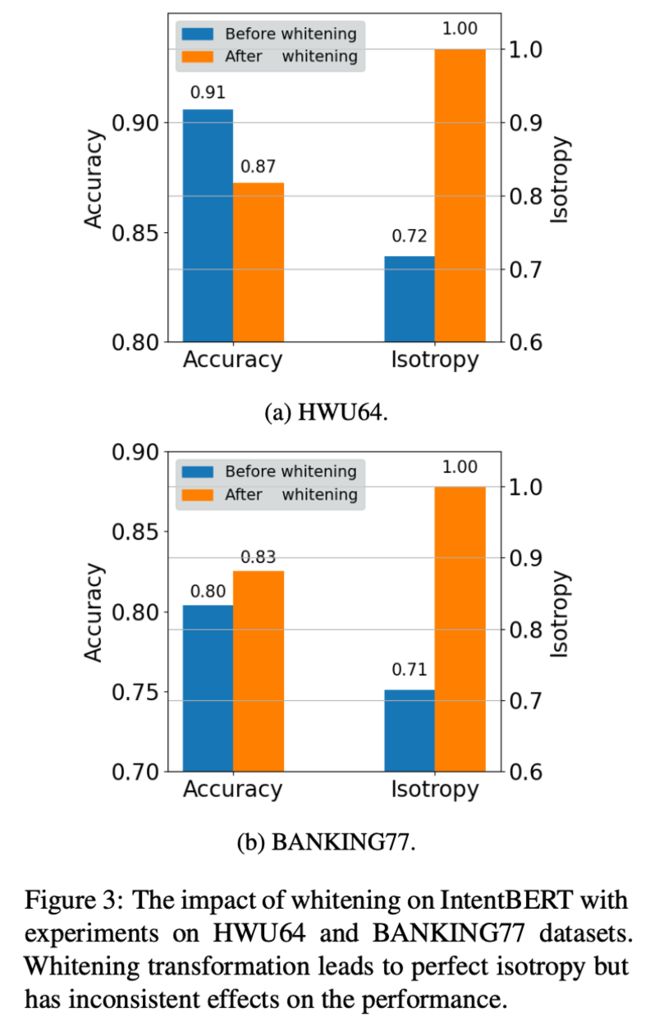
应用到 fine-tuned PLM 上的效果，如图 2、3 所示，可以看到除了 Figure 3(b)，其他结果都是模型的各向同性提高，在任务上的性能下降，这表明各向同性技术可能降低 fine-tuned PLM 的性能。

Method

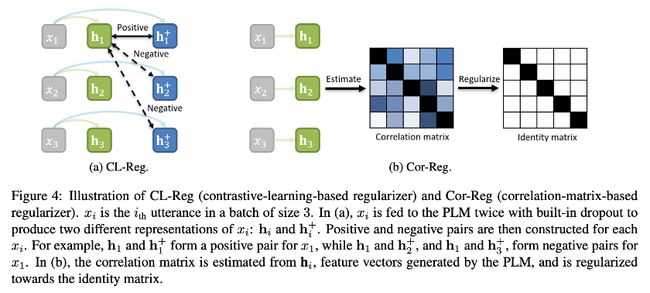
鉴于各向同性技术可能降低 fine-tuned PLM 的性能，于是作者便将各向同性技术与训练过程相结合，并提出了两种正则化方法，如图 4 所示，让模型在训练过程中更加各向同性。

1. Supervised Pre-training for Few-shot Intent Detection

现在的意图识别模型基本上是 PLM 加一个分类器（一般是线性层），设输入句子经 PLM 后的语义表示为 ${\mathbf{h}}_i$ ，则分类器的计算过程可描述为：

$\mathrm{p}\left(y\mid {\mathbf{h}}_i\right)=\mathrm{softmax}\left(\mathbf{W}{\mathbf{h}}_i+\mathbf{b}\right)\in {\mathbb{R}}^L$ (3)

其中${\mathbf{h}}_i\in {\mathbb{R}}^d$，$\mathbf{W}\in {\mathbb{R}}^{L\times d}$，$\mathbf{b}\in {\mathbb{R}}^L$，$L$是意图类别的数量。

模型参数训练过程可描述为：

$\theta =\underset{\theta }{\mathrm{argmin}}{\mathcal{L}}_{\mathrm{c}\mathrm{e}}\left({\mathcal{D}}_{\text{source }};\theta \right)$ (4)

其中${\mathcal{L}}_{\mathrm{c}\mathrm{e}}$为交叉熵损失函数，${\mathcal{D}}_{\text{source }}$是训练集。

2. Regularizing Supervised Pre-training with Isotropization

论文提出的方法就是给目标函数加上正则项（regularizer），以增加各向同性：

$\mathcal{L}={\mathcal{L}}_{\text{ce }}\left({\mathcal{D}}_{\text{source }};\theta \right)+\lambda {\mathcal{L}}_{\text{reg }}\left({\mathcal{D}}_{\text{source }};\theta \right)$ (5)

其中 $\lambda$ 是权重参数。

Contrastive-learning-based Regularizer

第一种正则项用的是上面提到过的 dropout-based contrastive learning loss，不过刚才是应用在 fine-tuned PLM 上，这里是用在 fine-tuning 中：

${\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{g}}=-\frac{1}{N_b}{\sum }_i^{N_b}\log \frac{e^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_i^{+}\right)/\tau }}{{\sum }_{j=1}^{N_b}{e}^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_j^{+}\right)/\tau }}$ (6)

$x_i$ 是 ${\mathcal{D}}_{\text{source }}$ 中的一条数据，$x_i$ 输入 PLM 两次，使用不同的 dropout masks 来得到两个不同的表示 ${\mathbf{h}}_i$和${\mathbf{h}}_i^{+}$，$\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_i^{+}\right)$ 是余弦相似度，因为${\mathbf{h}}_i$ 和 ${\mathbf{h}}_i^{+}$ 表示同一个输入，所以它们算是 positive pair，${\mathbf{h}}_i$ 和 ${\mathbf{h}}_j^{+}$ 就是 negative pair，前面说过，各向异性的特征向量都挤在一起，彼此距离很近，加了正则项后，在训练时，positive pairs 距离变近，negative pairs 距离变远，特征空间就更加各向同性。

Correlation-matrix-based Regularizer

上面的基于对比学习的正则项属于隐式的方法，论文还介绍了一种显式的方法。理想的各向同性是向量在特征空间内均匀分布，即特征向量的各维度相互之间具有零协方差和均匀方差，可以表示为一个具有均匀对角线元素和零非对角线元素的协方差矩阵。可以直接对模型的特征向量加上静态特征来达到各向同性，但尺度不好把握，于是作者将模型特征空间与理想各向同性的差距作为目标函数的正则项：

${\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{g}}=\Vert \mathbf{\Sigma }-\mathbf{I}\Vert$ (7)

其中$\Vert \cdot \Vert$是Frobenius norm，$\mathbf{I}\in {\mathbb{R}}^{d\times d}$是单位矩阵，$\mathbf{\Sigma }\in {\mathbb{R}}^{d\times d}$是相关矩阵，特征空间与理想各向同性差距越大，${\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{g}}$ 越大。

同时使用上面两种正则项得到：

$\begin{array}{r}\mathcal{L}={\mathcal{L}}_{\text{ce }}\left({\mathcal{D}}_{\text{source }};\theta \right)+{\lambda }_1{\mathcal{L}}_{\text{cl }}\left({\mathcal{D}}_{\text{source }};\theta \right)+{\lambda }_2{\mathcal{L}}_{\text{cor }}\left({\mathcal{D}}_{\text{source }};\theta \right)\end{array}$ (8)

论文中实验结果表明两种正则项一起用效果更好。

实验设置及结果

1. 实验设置

数据集

论文中使用了 OOS 数据集作为训练和验证数据集，其包含 10 个领域共 150 个意图类别，作者去除了其中的“Banking”和“Credit Cards”两个领域的数据，因为这两个领域的数据跟测试集 BANKING77 在语义上比较相似，剩下的 8 个领域里，6 个用作训练集，2 个用作验证集，如表 2 所示。

论文使用下面几个数据集作为测试集，数据集的统计信息如表 3 所示：

• BANKING77：关于银行服务的意图识别数据集；
• HINT3：覆盖 3 个领域，“Mattress Products Re- tail”、“Fitness Supplements Retail”和“Online Gaming”；
• HWU64：包含21个领域的大规模数据集。

参数设置

论文中方法使用的 PLM 为 BERT 和 RoBERTa，取 [CLS] 位置的输出作为公式(3)中的表示，用逻辑回归做分类，通过验证集选择合适的参数，参数设置如表4所示。

基线模型

基于 BERT 的有 BERT-Freeze（冻结 off-the-shelf PLM）、IntentBERT（用公开的意图识别数据对 BERT进行有监督预训练），IntentBERT-ReImp 是作者为了公平比较而复现的 IntentBERT，还有下面几个用对话语料或 NLI 数据继续预训练过的模型：

• CONVBERT
• TOD-BERT
• DNNC-BERT
• USE-ConveRT
• CPFT-BERT

基于 RoBERTa 的模型有：

• RoBERTa-Freeze
• WikiHowRoBERTa
• DNNC-RoBERTa
• CPFT-RoBERTa
• IntentRoBERTa

最后，作者把 whitening transformation 应用在 PLM 上，以跟论文方法作对比：

• BERT-White
• RoBERTa-White
• IntentBERT-White
• IntentRoBERTa-White

训练细节

• Pytorch、Python
• Hugging Face的bert-base-uncased和roberta-base
• Adam 优化器，学习率 2e-05，weight decay 为 1e-03
• Nvidia RTX 3090 GPUs
• 在验证集上 100 步没有提升就停止训练
• 随机种子集合 {1, 2, 3, 4, 5}

评价

在 C-way K-shot 任务上做测试，即对于每个任务，取其中的 C 个意图类别，每个类别 K 条数据，用这 $C\times K$ 条数据训练模型。然后每个类别取 5 条数据作为 queries，比较所用的结果是从${\mathcal{D}}_{\text{target}}$ 里随机选取的 500 个任务上的平均准确率（averaged accuracy）。

2. Main Results

实验结果如表 5、表 6 所示，可以看到论文提出的方法的结果优于其他方法，Cor-Reg 的结果优于 CL-Reg，两种正则项共同使用又能得到更好的结果。

论文中还对比了用论文方法训练的模型跟一般模型的各向同性的不同，可以看到模型的各向同性和其在任务上的性能成正比。

3. 消融实验和分析

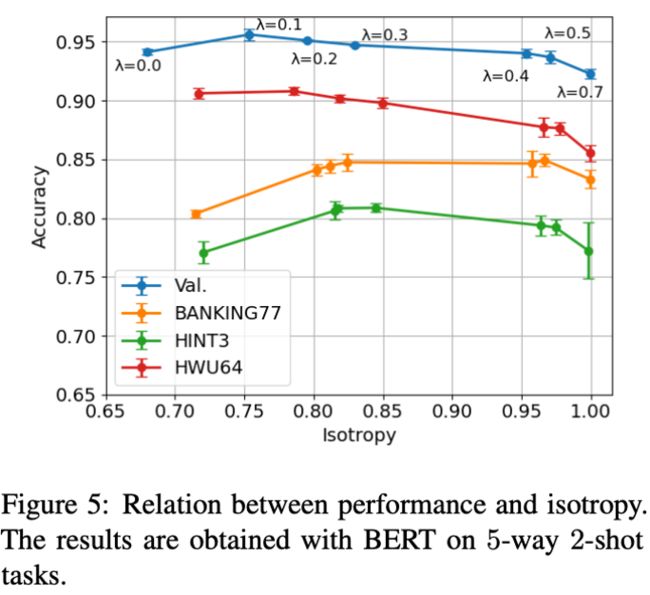
Moderate isotropy is helpful

作者探究了各向同性跟 few-shot intent detection 任务上的性能的关系，其调整 Cor-Reg 的权重得到更高的各向同性，然后测试模型性能，结果如图 5 所示，可以看出中等大小各向同性的模型性能较好。

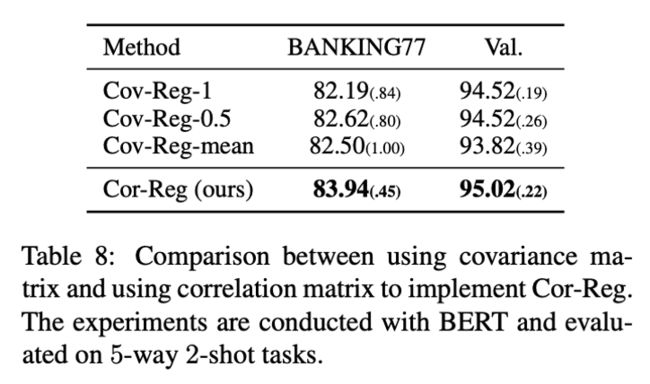
Correlation matrix is better than covariance matrix as regularizer

作者在 Cor-Reg 里用的是相关矩阵而不是协方差矩阵，尽管协方差矩阵比相关矩阵多了方差的信息，但正因为如此，让人难以决定各个方差的尺度。在实验中，作者将相关矩阵换成协方差矩阵，原来的单位矩阵里的非对角线元素设为 0，对角线元素设为 1、0.5 或者协方差矩阵对角线元素的平均值，表示为 Cov-Reg-1、Cov-Reg-0.5、和 Cov- Reg-mean，实验结果如表8所示，可以看到协方差矩阵的几种设置都比相关矩阵要差一些。

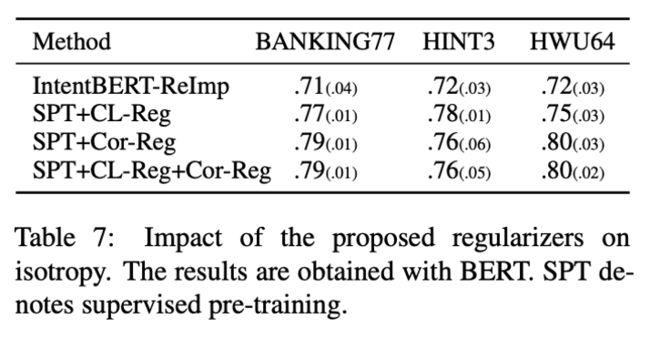
The performance gain is not from the reduction in model variance

L1 和 L2 正则化可以通过减小模型方差来提升性能，而作者将表 7 里的性能提升归因于各向同性的改善。为了探究使用了正则项后性能的提升是来自方差还是各向同性，作者给 L2正 则项设置不同的权重，得到多个结果，但都不及 CL-Reg 和 Cor-Reg，如图 6 所示。

The computational overhead is small

作者统计了同时使用 CL-Reg 和 Cor-Reg 的时候，一个 epoch 里各个计算过程的开销，比例如图 7 所示，可以看到正则项的计算开销占比并不算太大。

总结

这篇论文先分析了 PLM 在意图识别任务上微调后、其特征空间的各向异性，然后提出了分别基于对比学习和相关矩阵的两种正则项，以在微调中增加模型特征空间的各向同性，并且给模型在 few-shot intent detection 任务上的性能带来了很大的提升。因为论文提出的方法是针对 PLM 的，所以也可能用于其他任务的基于 PLM 的模型上。感兴趣的同学可以自行阅读论文原文，欢迎留言讨论。

参考文献

[1] Zhang H, Zhang Y, Zhan L M, et al. Effectiveness of Pre-training for Few-shot Intent Classification[C]//Findings of the Association for Computational Linguistics: EMNLP 2021. 2021: 1114-1120.

[2] Rajaee S, Pilehvar M T. An Isotropy Analysis in the Multilingual BERT Embedding Space[J]. arXiv preprint arXiv:2110.04504, 2021.

[3] Zhou W, Lin B Y, Ren X. IsoBN: fine-tuning BERT with isotropic batch normalization[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021, 35(16): 14621-14629.

[4] Gao T, Yao X, Chen D. SimCSE: Simple Contrastive Learning of Sentence Embeddings[C]//Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. 2021: 6894-6910.

[5] Su J, Cao J, Liu W, et al. Whitening sentence representations for better semantics and faster retrieval[J]. arXiv preprint arXiv:2103.15316, 2021.