机器学习笔记—朴素贝叶斯算法(matlab/python)
原理知道一百遍不如自己动手写一遍,当然,现在基本上不需要自己来写算法的底层code了,各路大神们已经为我等凡夫俗子写好了,直接调用就行。
这里介绍在MATLAB中和Python中应用贝叶斯算法的小例子。
一、 matlab实现朴素贝叶斯算法
先load matlab中自带的数据集
load fisheriris
X = meas(:,3:4);
Y = species;
tabulate(Y)%返回概率表格
接下来用朴素贝叶斯算法进行拟合,大家可以注意下matlab的机器学习算法的命名规则,都是以’fit’开头,中间一个字母’c’或者‘r’,c’代表是分类算法(classification),'r’代表回归算法(regression),后面的字母就是算法的通用名称。
以下是对X、Y进行拟合,指定Y变量中分类的名称分别为’setosa’,‘versicolor’和’virginica’
Mdl = fitcnb(X,Y,'ClassNames',{'setosa','versicolor','virginica'})
Mdl =
ClassificationNaiveBayes
ResponseName: ‘Y’
CategoricalPredictors: []
ClassNames: {‘setosa’ ‘versicolor’ ‘virginica’}
ScoreTransform: ‘none’
NumObservations: 150
DistributionNames: {‘normal’ ‘normal’}
DistributionParameters: {3x2 cell}
这里返回了贝叶斯分类器的各种参数,包含分类名称、数据行数是否归一化等。
在matlab中,默认每一个特征的都符合高斯分布,拟合结果中也计算了每一个特征的均值和方差。
假如我们想看分类为‘setosa’类的X的第一个特征的均值和方差。
setosaIndex = strcmp(Mdl.ClassNames,'setosa');
estimates = Mdl.DistributionParameters{setosaIndex,1}
estimates =
1.4620
0.1737
均值是1.4620,方差是0.1737
接下来我们将拟合结果可视化,让大家更直观地感受拟合效果。
figure 打开一个新的画布
gscatter(X(:,1),X(:,2),Y);%画出散点图
h = gca;
cxlim = h.XLim;%获取x轴坐标
cylim = h.YLim; %获取y轴坐标
hold on
Params = cell2mat(Mdl.DistributionParameters);%获取高斯分布的参数
Mu = Params(2*(1:3)-1,1:2); % 提取均值列
Sigma = zeros(2,2,3);
for j = 1:3
Sigma(:,:,j) = diag(Params(2*j,:)).^2; % Create diagonal covariance matrix
xlim = Mu(j,1) + 4*[1 -1]*sqrt(Sigma(1,1,j));
ylim = Mu(j,2) + 4*[1 -1]*sqrt(Sigma(2,2,j));
ezcontour(@(x1,x2)mvnpdf([x1,x2],Mu(j,:),Sigma(:,:,j)),[xlim ylim])
% 绘制多元正态分布的等高线
end
h.XLim = cxlim;%设置X轴显示范围
h.YLim = cylim;%设置Y轴显示范围
title('Naive Bayes Classifier -- Fisher''s Iris Data')
xlabel('Petal Length (cm)')
ylabel('Petal Width (cm)')
hold off
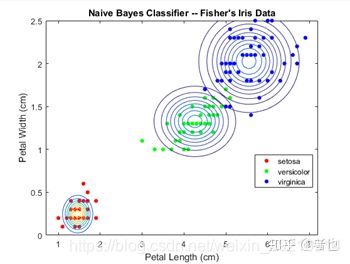
默认情况下,先验类概率分布是根据数据集计算的各类的相对频率分布,在这种情况下,对于每个分类,其相对频率分布均为33%。但是假如你知道在总样本中50%的’ setosa’,20%是’versicolor’,30%’ ViGiCina’。你可以在训练分类器的时候指定先验概率。
prior = [0.5 0.2 0.3];
Mdl = fitcnb(X,Y,'ClassNames',classNames,'Prior',prior)%指定每一类的概率
使用10倍交叉验证估计两个模型的交叉验证误差。
rng(1); % For reproducibility
defaultCVMdl = crossval(defaultPriorMdl);
defaultLoss = kfoldLoss(defaultCVMdl)
CVMdl = crossval(Mdl);
Loss = kfoldLoss(CVMdl)
二、 Python(sklearn实现贝叶斯算法)
1. 利用GaussianNB类建立简单模型
import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1, -1], [-2, -2], [-3, -3],[-4,-4],[-5,-5], [1, 1], [2,2], [3, 3]])
y = np.array([1, 1, 1,1,1, 2, 2, 2])
clf = GaussianNB() #默认priors=None
clf.fit(X,y)
GaussianNB(priors=None)
2. 经过训练集训练后,观察各个属性值
clf.priors #无返回值,因priors=None
clf.set_params(priors=[0.625, 0.375]) #设置priors参数值
GaussianNB(priors=[0.625, 0.375])
clf.priors #返回各类标记对应先验概率组成的列表
clf.class_count_ #获取各类标记对应的训练样本数
clf.sigma_ #获取各个类标记在各个特征上的方差
算法类文章我都会同期更新到个人公众号:宽客塔,欢迎关注~~
这个公众号以前是写金融类消息的,后来因为个人转行,就改为分享机器学习算法知识,也算是边学边写,跟大家共同学习~