功能磁共振成像统计分析中的 GLM 简介

什么是功能磁共振成像？

功能性磁共振成像 (fMRI) 是基于这样一个事实，即当局部神经活动增加时，新陈代谢和血流的增加会导致氧合血红蛋白（血液中携带氧气的红细胞）和脱氧血红蛋白（相同输送氧气后的红细胞）。氧合血红蛋白和脱氧血红蛋白具有不同的磁性（分别为抗磁性和顺磁性），它们以不同方式影响局部磁场。 MRI 扫描仪采集的信号对局部磁场的这些变化很敏感。为了记录功能会话期间的大脑活动，扫描仪被调整以检测这种“血氧水平依赖性”（BOLD）信号。

大脑活动的测量时间跨度为几分钟，在此期间参与者执行一些认知任务，扫描仪采集大脑图像，通常每 2 或 3 秒一次（两次连续图像采集之间的时间称为重复时间，或 TR）。
大脑 MR 图像提供大脑的 3D 图像，可以分解为体素（相当于像素，但为 3 维）。在功能会话期间获取的一系列图像在每个体素中提供了表示 MRI 信号的正实数时间序列，在 TR 处采样。

注意 在使用 fMRI 图像进行有意义的比较之前，必须对其进行处理以确保被比较的体素代表相同的大脑区域，而不管实验中不同受试者的大脑大小和形状及其微架构的变化。该过程称为空间配准或空间归一化。在此过程中，所有大脑图像的体素都被“注册”以对应于大脑的同一区域。通常，图像（它们的体素）被注册到一个标准的“模板”大脑图像（它的体素）。一种常用的标准模板是蒙特利尔神经病学研究所的 MNI152 模板。完成此操作后，体素的坐标与模板在同一空间中，并可用于使用基于同一模板的大脑图谱来估计其大脑位置。如前所述，nilearn 包不执行空间预处理；它只对体素时间序列进行统计分析。对于预处理功能，可参考 Nipype 或 fMRIPrep。

功能磁共振成像数据建模

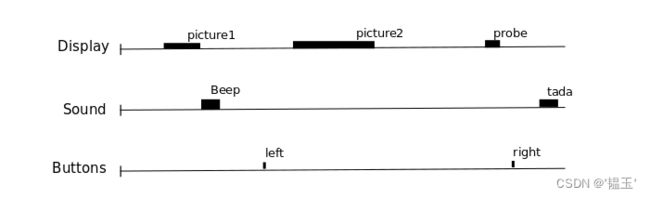
分析时间序列的一种方法是将它们与根据我们对功能会话期间发生的事件的知识构建的模型进行比较。事件可以对应于参与者的动作（例如按下按钮）、感官刺激的呈现（例如声音、图像）或假设的内部过程（例如记忆刺激）。

人们预计参与处理某种类型事件的大脑区域（例如听觉皮层的声音）会显示出与这些事件的时间图相关的激活时间过程。如果 fMRI 信号直接显示神经活动并且不包含任何噪声，我们可以在各种体素中查看它并检测那些符合时间图的体素。

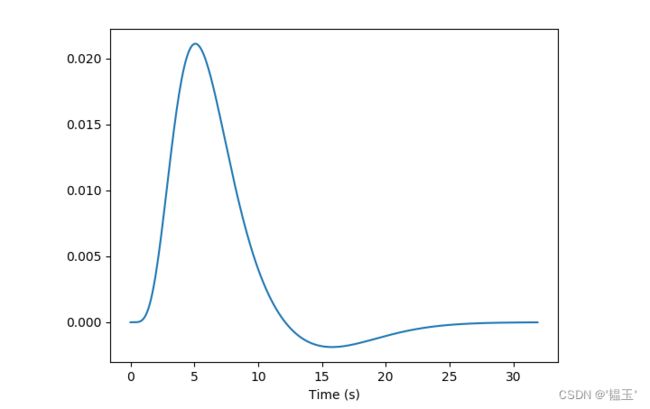
但是我们从之前的测量中知道，BOLD 信号不遵循刺激处理的确切时间过程和潜在的神经活动。 BOLD 反应反映血流量和氧脱氧血红蛋白浓度的变化，共同形成缓慢而持久的血流动力学反应，如下图所示，显示了对冲动事件的反应（例如，向参与者播放的听觉点击）。

 

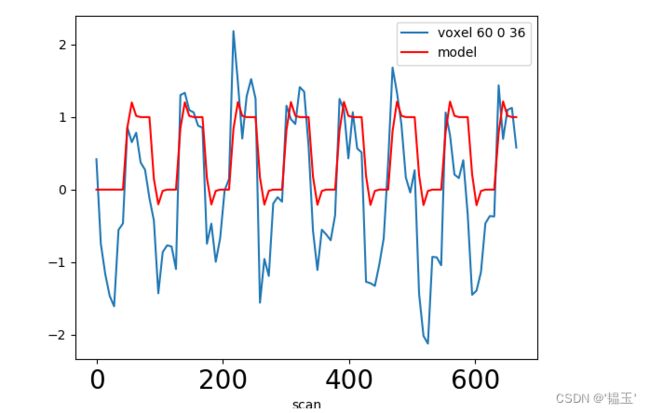
利用我们对血流动力学响应的了解，我们可以根据事件的时间图构建预测的时间进程（该操作称为卷积；简单地说，它测量一个函数图的形状如何影响另一个函数图的形状.。注：它假设 BOLD 响应的线性，在某些情况下可能是错误的假设，比如相邻刺激时间很短）。正是这个预测的时间过程，也称为预测器，与实际的 fMRI 信号进行比较。如果预测变量和信号之间的相关性高于预期的机会水平，则表示体素对事件类型表现出显着响应。 

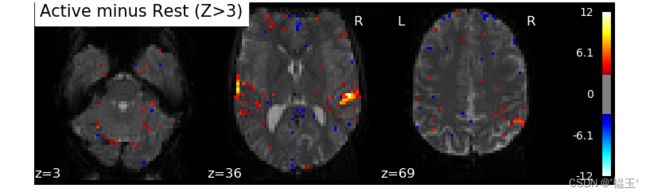
 在每个体素处分别计算相关性，并且可以生成相关性图，以显示每个体素处的相关性值（-1 和 +1 之间的实数）。然而，一般来说，论文中提供的地图报告了每个体素的相关性的显着性，使用 T、Z 或 p 值进行无相关性的零假设检验。例如，下图显示了一个 Z-map，显示了响应听觉事件的体素。大（正或负）值不太可能仅是由于偶然性。对地图进行阈值处理，以便仅对 p 值小于 1/1000 的体素着色。

在大多数 fMRI 实验中，需要几个预测因子来完整描述会话期间发生的事件——例如，实验者可能想要区分与听觉刺激感知和按钮按下相关的大脑活动。为了找到每个预测变量的特定效果，通常使用多元线性回归方法：所有预测变量都作为设计矩阵中的列输入，软件会找到这些列的最适合信号的线性组合。通过该线性组合分配给每个预测器的权重是该预测器对体素响应的贡献的估计。可以使用效果大小图或显示其统计意义的图（在没有效果的零假设下它们不太可能）来绘制这一点 

 简而言之，fMRI 图像的分析包括：

1.根据按类型分组、在特定时间发生并具有特定持续时间的事件来描述范式。
2.为每种类型的事件创建预测因子，通常使用血流动力学响应的卷积。
3.将这些预测器组装到一个设计矩阵中，提供一个线性模型。
4.使用线性回归估计模型的参数，即与每个体素上的每个预测变量相关的权重。
5.显示系数或它们的线性组合，和/或它们的统计意义。

功能磁共振成像统计分析

如上一节所述，fMRI 的基本统计分析在概念上是一种相关性分析，其中确定设计矩阵的列的某种组合（对比度）是否适合给定位置的 fMRI 信号的显着比例。
可以看出，这相当于研究估计的对比度效应是否相对于其确切值的不确定性很大。具体来说，我们计算效果大小估计值及其值的不确定性并将两者相除。结果数字没有物理维度，它是一个统计量，a Student or t-statistic，我们用 t 表示。接下来，基于 t，我们要确定真实效果是否确实大于零。

如果真实效果为零，则 t 不一定为 0：偶然地，数据中的噪声可能部分由感兴趣的对比来解释。但是，如果我们假设噪声是高斯的并且模型是正确指定的，那么我们知道 t 应该遵循具有dof自由度的Student分布，其中 dof 是模型中自由参数的数量：在实践中，观察数（即时间点数），n_scans 减去设计矩阵的建模效果数（即 n_columns 列数）：

dof = n_scans - n_columns

有了这个，我们可以进行统计推断。给定一个预定义的错误率α，我们将观察到的 t 与具有dof自由度的Student分布的 (1-α) 分位数进行比较。如果 t 大于这个数字，我们可以用 p 值 α 拒绝原假设；意思是，如果没有影响，观察到与 t 一样大的影响(effect)的概率将小于 α。

 

Multiple Comparisons

 这里出现的一个众所周知的问题是多重比较：当一个统计测试被重复很多次时，比如每个体素一个，即 n_voxels 次，那么人们可以预期，在没有任何影响的情况下，数量检测数——因为没有效果而导致的错误检测——大约为 n_voxels*。如果 =.001 且 n=10^5，错误检测的数量将约为 100。危险在于人们可能不再信任检测，即 z 的值大于 (1-)-分位数的标准正态分布。

人们可能会想到的第一个想法是取小得多的 ：例如，如果我们取 , 那么预期的错误发现数仅为 0.05 左右，这意味着真正不活跃的体素有 5% 的机会被宣布为活跃。这种对显着性的校正称为 Bonferroni 程序。当不同的测试独立或接近独立时，它是相当准确的，但如果不是，则变得保守。这种方法的问题在于，真正激活的体素可能不会超过相应的阈值，该阈值通常非常高，因为 n_voxels 很大

 第二种可能是选择一个阈值，使得发现中真实发现的比例达到一定比例0

还要注意，超过阈值的体素集通常被收集到连接的组件（也称为集群）中，因此只有大的连接组件被保留，而孤立的超阈值体素被丢弃。基本原理是孤立的体素不太可能代表扩展的大脑区域，并且很可能是噪音。因此，丢弃它们通常可以提高结果的质量和可靠性。