跟我学神经网络1-前向传播
目录
-
- 1. 关键词
- 2. 导读
- 3. 神经网络
-
- 3.1 来源
- 3.2 组成
-
- 3.2.1 神经元
- 3.2.2 激活函数
- 4. 多层感知器
- 5. 前向传播
- 6. 附录
-
- 6.1 中英文对照表
- 6.2 扩展阅读
欢迎关注《汽车软件技术》公众号,回复关键字获取资料。
1. 关键词
神经网络,激活函数,多层感知器,前向传播
2. 导读
本文是《跟我学神经网络》系列文章的第1篇,介绍神经网络的结构和前向传播过程。
《跟我学神经网络》不在大而全,而是给读者一个更感性的认识,特别是一些很难理解的专有名词。当你有兴趣,想要进一步学习,可以参考文末的扩展阅读部分。
3. 神经网络
3.1 来源
神经网络灵感来自于生物大脑,由大量的神经元和突触组成。引入神经网络,旨在解决非线性问题。
3.2 组成
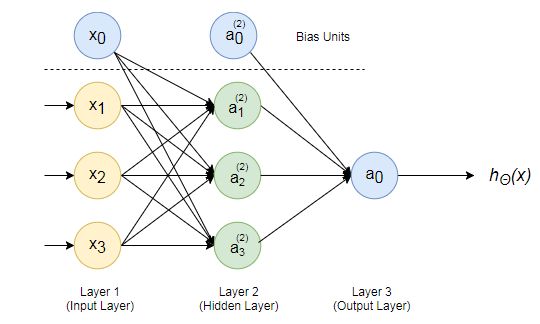
上图是一个典型的3层结构神经网络:输入层、隐含层和输出层。每层都有1个或多个神经元构成,神经元之间由边连接。边对应于权重。
- 输入层:4个神经元,其中x0是偏置单元;
- 隐含层:4个神经元,其中a0是偏置单元;
- 输出层:1个神经元。
3.2.1 神经元
上图是一个典型的神经元,包含:输入、权重、求和、激活函数、输出。公式如下:
y = g ( z ) , z = ∑ j = 1 n x j ω j y=g(z),z=\sum\limits_{j=1}^{n}x_j\omega_j y=g(z),z=j=1∑nxjωj
其中:
- y y y,输出;
- g g g,激活函数;
- z z z,输入加权求和;
- x x x,输入;
- ω \omega ω,权重;
- j j j,第 j j j 个输入;
- n n n,输入总数。
并非每个神经元都包含全部,见下表。
| 神经元 | 构成 |
|---|---|
| 偏置单元 | 输出 |
| 输入层非偏置单元 | 输入、输出 |
| 隐含层非偏置单元 | 全部 |
| 输出层 | 全部 |
其中,偏置单元相当于引入的一个常数项,类似于方程的截距( y = a x + b y=ax+b y=ax+b 中的 b b b)。
3.2.2 激活函数
激活函数可以理解为输入加权求和后,到输出的一个阈值。这也是模仿了生物神经系统,神经脉冲传导需要达到一定的电平。比如常用的 sigmoid 激活函数,公式如下:
g ( z ) = 1 1 + e z g(z)=\frac1{1+e^z} g(z)=1+ez1
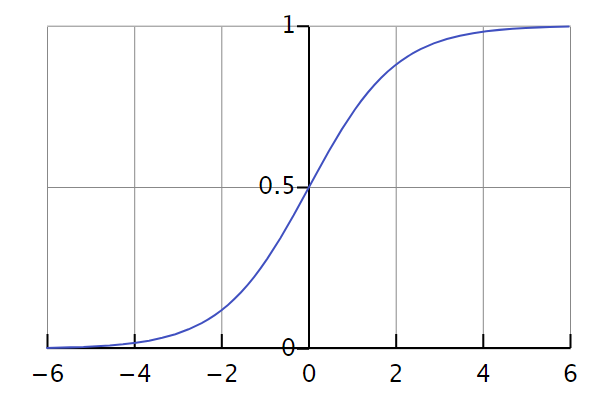
曲线如下:
从图中可以看出,只有当 z z z 超过一定值时,输出才会是1。
4. 多层感知器
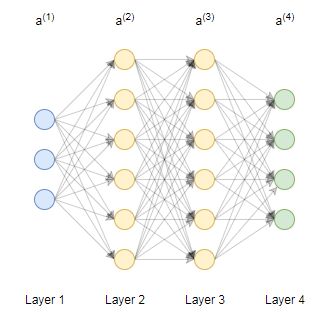
实际问题中通常需要多层、很多神经元构成的神经网络,比如下图中的4层神经网络。
常用的图像识别,输入层神经元的数量和图像的像素数等同。
5. 前向传播
在第2个部分介绍了单个神经元的数据传播,那么对于整个网络呢?数据从输入层传递到输出层,这个过程叫做前向传播。以上面的4层网络为例,写成向量形式,前向传播步骤如下:
a ( 1 ) = x z ( 2 ) = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) + a 0 ( 2 ) z ( 3 ) = Θ ( 2 ) a ( 2 ) a ( 3 ) = g ( z ( 3 ) ) + a 0 ( 3 ) z ( 4 ) = Θ ( 4 ) a ( 4 ) a ( 4 ) = h ( x ) = g ( z ( 3 ) ) \begin{aligned} a^{(1)}&={x}\\ z^{(2)}&=\Theta^{(1)}{a^{(1)}}\\ a^{(2)}&=g(z^{(2)})+a_0^{(2)}\\ z^{(3)}&=\Theta^{(2)}{a^{(2)}}\\ a^{(3)}&=g(z^{(3)})+a_0^{(3)}\\ z^{(4)}&=\Theta^{(4)}{a^{(4)}}\\ a^{(4)}&=h(x)=g(z^{(3)}) \end{aligned} a(1)z(2)a(2)z(3)a(3)z(4)a(4)=x=Θ(1)a(1)=g(z(2))+a0(2)=Θ(2)a(2)=g(z(3))+a0(3)=Θ(4)a(4)=h(x)=g(z(3))
其中:
- x x x,输入;
- Θ ( i ) \Theta^{(i)} Θ(i),第 i i i 层到下一层的权重;
- a 0 ( i ) a_0^{(i)} a0(i),第 i i i 层的偏置单元;
- a ( i ) a^{(i)} a(i),第 i i i 层输出;
- z ( i ) z^{(i)} z(i),第 i i i 层输入加权和;
- h ( x ) h(x) h(x),输入对应的预测值,也就是最终的输出。
神经网络的目的是在已知输入和正确输出数据的情况下,用数据训练模型,得到一组权重参数,使得模型输出和正确输出一致。之后,再利用这个模型,对新的数据进行预测。在前向传播时,很难去求解这组参数,因此引入了反向传播。
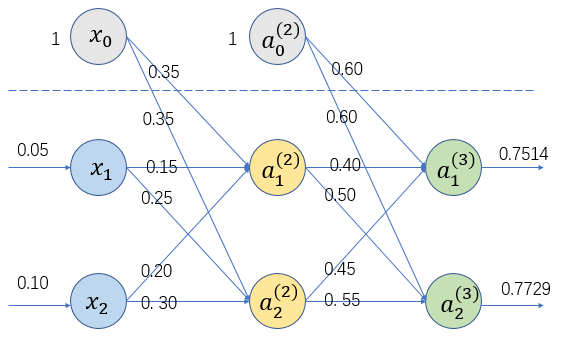
下面通过一个例子,进一步熟悉计算过程,所有参数已列在图上。
输入:
x = [ 0.05 , 0.10 ] T x=[0.05,0.10]^T x=[0.05,0.10]T
隐含层偏置0.35,输出层偏置0.60。
输入层到隐含层权重:
Θ ( 1 ) = ( 0.15 0.20 0.25 0.30 ) \Theta^{(1)}=\left( \begin{matrix} 0.15 & 0.20\\ 0.25 & 0.30\\ \end{matrix} \right) Θ(1)=(0.150.250.200.30)
隐含层到输出层权重:
Θ ( 2 ) = ( 0.40 0.45 0.50 0.55 ) \Theta^{(2)}=\left( \begin{matrix} 0.40 & 0.45\\ 0.50 & 0.55\\ \end{matrix} \right) Θ(2)=(0.400.500.450.55)
可以手动计算,或者运行如下的 Python 代码:
import numpy as np
# 激活函数 sigmoid
def sigmoid(input):
return 1 / (1 + np.exp(-input))
# 层计算
def layer(input, weight, isInputLayer, bias):
output = input
if weight is not None:
output = np.dot(weight, input)
if bias is not None:
output = output + bias
if not isInputLayer:
output = sigmoid(output)
return output
# 输入
x = np.array([0.05, 0.10])
# 输入层偏置单元
x0 = 0.35
# 输入层到隐含层权重
thelta_1 = np.array([[0.15, 0.20],
[0.25, 0.30]])
# 隐含层偏置单元
a_0_2 = 0.6
# 隐含层到输出层权重
thelta_2 = np.array([[0.40, 0.45],
[0.50, 0.55]])
# 输入层
a_1 = layer(x, None, True, None)
print(a_1)
# 隐含层
a_2 = layer(a_1, thelta_1, False, x0)
print(a_2)
# 输出层
a_3 = layer(a_2, thelta_2, False, a_0_2)
print(a_3)
输出结果:
[0.05 0.1 ]
[0.59326999 0.59688438]
[0.75136507 0.77292847]
6. 附录
6.1 中英文对照表
| 英文 | 中文 | 缩写 | 数学符号 |
|---|---|---|---|
| Activation Function | 激活函数(激励函数) | - | g ( z ) g(z) g(z) |
| Artificial Neural Network | 人工神经网络 | ANN | |
| Bias Unit | 偏置单元(截距单元) | - | a 0 ( i ) a_0^{(i)} a0(i) |
| Edge | 边 | - | |
| Forward Propagation | 前向传播 | - | |
| Hidden Layer | 隐含层 | - | |
| Image Recognition | 图像识别 | - | |
| Input Layer | 输入层 | - | |
| Multilayer Perceptron | 多层感知器 | MLP | |
| Neural Network | 神经网络 | NN | |
| Neuron | 神经元 | - | y = g ( z ) , z = ∑ j = 1 n x j ω j y=g(z),z=\sum\limits_{j=1}^{n}x_j\omega_j y=g(z),z=j=1∑nxjωj |
| Output Layer | 输出层 | - | |
| Weight | 权重 | - | 单个值: ω \omega ω,向量/矩阵: Θ \Theta Θ |
6.2 扩展阅读
- 吴恩达机器学习课程(公众号回复“吴恩达”获取视频和笔记)
- 3Blue1Brown-神经网络