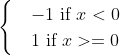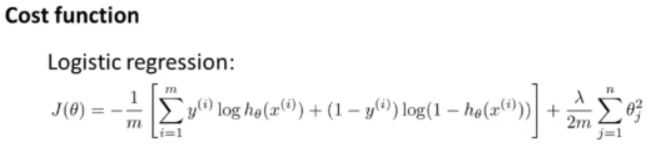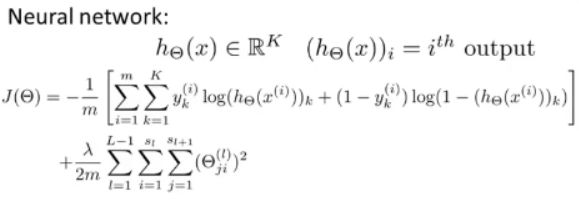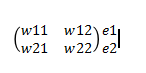神经网络介绍
一、为什么要学习神经网络
因为之前所学的分类算法,比如线性回归、逻辑回归等,都有一个缺点,即:当特征太多时,计算的负荷会很大。
二、模型表示
2.1 概述
神经网络是一种仿生模型。我们先介绍一下生物神经网络:
神经元--可以接收、发射脉冲信号的细胞
树突--接收其他神经元的脉冲信号
轴突-将神经元的输出脉冲传递给其他神经元
突触--发生信息的交换传递
在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变神经元内的点位,如果某个神经元的电位超过了一个阈值,那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。
上述情形抽象为M-P神经元模型。在这个模型中,神经元接收到来自n个其他神经元传递过来的信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”处理以产生神经元的输出。
对下图进行分析:输入可以类比为神经元的树突,加权求和可以类比为细胞体,激活函数类比为轴突,输出值y类比为突触。求和是线性操作,激活函数是非线性的。
一个问题:为什么激活函数是非线性的,能去掉这一部分吗?
一个回答:激活函数之所以是非线性的是为了处理非线性问题,不能去掉,如果去掉了,无论神经网络的层数有多少,也只是一直在进行线性操作。
![]()
2.2 感知机介绍
1、感知机模型(单层神经网络)
感知机是一种二类分类的线性分类模型。感知机的思想很简单,比如我们在一个平台上有很多的男孩女孩,感知机的模型就是尝试找到一条直线,能够把所有的男孩和女孩隔离开。放到三维空间或者更高维的空间,感知机的模型就是尝试找到一个超平面,能够把所有的二元类别隔离开。
用数学的语言来说,如果我们有m个样本,每个样本对应于n维特征和一个二元类别输出,如下:
(![]() ),(
),(![]() )........
)........![]()
我们的目标是找到一个超平面,即![]() ,将正负样本分开,即能够将数据集的正实例点和负实例点正确地划分到这个超平面的两侧。当然显然不是唯一的。
,将正负样本分开,即能够将数据集的正实例点和负实例点正确地划分到这个超平面的两侧。当然显然不是唯一的。
为了简化超平面写法,增加一个特征x0=1,使超平面变为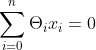 ,进一步向量表示为
,进一步向量表示为![]() 。所以感知机的模型可以定义为:y=sign(
。所以感知机的模型可以定义为:y=sign(![]() ),其中:sign(x)=
),其中:sign(x)=
2、感知机模型损失函数
我们损失函数的优化目标,就是期望使误分类的所有样本,到超平面的距离之和最小。
3、感知机模型损失函数的优化方法
这个损失函数可以用梯度下降法或者拟牛顿法来解决,常用的是梯度下降法。但是用普通的基于所有样本的梯度和的均值的批量梯度下降法(BGD)是行不通的,原因在于我们的损失函数里面有限定,只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降,只能采用随机梯度下降(SGD)或者小批量梯度下降(MBGD)。感知机模型选择的是采用随机梯度下降,这意味着我们每次仅仅需要使用一个误分类的点来更新梯度。
如果我们找不到这么一条直线进行二分类的话怎么办?找不到的话那就意味着类别线性不可分,也就意味着感知机模型不适合你的数据的分类。使用感知机一个最大的前提,就是数据是线性可分的。这严重限制了感知机的使用场景。它的分类竞争对手在面对不可分的情况时,比如支持向量机可以通过核技巧来让数据在高维可分,神经网络可以通过激活函数和增加隐藏层来让数据可分
4、多层感知机MLP(两层神经网络)
两层神经网络包含一个输入层,一个输出层以及一个隐藏层。
注意:多层神经网络就是深度学习了。
2.3 神经网络损失函数
先回顾一下逻辑回归问题中的代价函数:
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),但是在神经网络中,我们可以有多个输出变量,即h(x)是一个维度为k的向量,神经网络的代价函数是:
虽然看起来复杂,但是背后的思想是一样的,希望通过代价函数来观察算法预测的结果与真实情况的误差有多大。不同的是,对于每一行特征,我们利用循环都会给出K个预测,然后再利用循坏在K个预测中选择可能性最高的一个,将其与y中实际数据相比。
含义:表示第i个输出,h(x)是一个k维向量,下标 i 表示选择输出神经网络输出向量中的第 i 个元素。
损失函数第一项:加入神经网络最后一层有四个输出单元,那么这个求和就是K从1到4的每一个逻辑回归算法损失函数之和。
损失函数第二项:类似于在逻辑回归里所用的正则化项,实际上是排除了第0项之后,每一层theta矩阵的和。
2.4 误差逆传播算法(BP)
多层网络的学习能力比单层感知机强得多,欲训练多层网络,简单感知机学习规则显然不够,需要更强大的算法,BP算法就是其中最杰出的算法。BP可以计算出神经网络代价函数的偏导数,进而用来优化神经网络的代价函数。
问:为什么不直接用梯度下降算法直接计算偏导项来更新参数呢?
答:可以利用梯度下降算法直接计算偏导数的形式来更新神经网络的每个参数,但是,在神经网络中,它的参数很多,会导致偏导数的计算量很大很复杂。所以引入了BP算法,将繁杂的导数计算替换为导数的链式法则计算,而链式法则的中间函数提供者是每个神经元的误差。
假设我们的训练集只有一个实例(x1,y1),神经网络是一个四层的。
首先看一下前向传播算法,前向传播算法得到代价函数J,如下:
一个问题:为什么要设置偏置项,即上面的a0
一个回答:是阈值,作用是控制激活的容易程度。(比如宴会上摆成金字塔型的酒杯,然后开始倒酒,显然只有上一层满了之后才会向下层流去,这个酒杯的容量其实就相当于偏置项的作用,设置阈值。)
误差
接下来看一下,我们知道输出的预测值和真实值之间是有误差的(这个误差是怎么来的呢,主要是来源于各个传递通道之间的权重W):
看一个简单的例子(只有输出层和输入层),来计算误差:
假设x1和x2是输入,w1和w2是权重,e是误差,则有x1输入对于误差构成的比例是0.2,x2输入对于误差构成的比例是0.8,这是由权重决定的,权重越大,在误差占比越大。
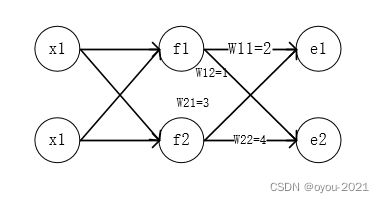
再看一个较复杂的例子(加一个隐藏层且多个输出)
e1,e2分别为0.8和0.5.计算单元误差如下:
上面的计算可以用矩阵形式表示出来,这个分母可以去掉,它的作用是归一化,不影响矩阵计算。那么如何减小误差呢,因为误差的主要来源是各传递的权重,所以问题转换为怎么改变权重,常用思想求偏导。
BP思想
怎么求误差关于权重的偏导呢--链式法则
假设是下面这样一个网络结构,预测输出o,真实输出为t。然后我们采用均方误差,公式是 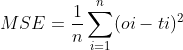
这个中间函数o是什么呢?![]() 补充,sigmoid的求导为f(1-f).
补充,sigmoid的求导为f(1-f).
下面用具体例子说明:
先前向
![]()
下面是反向传播(求网络误差对各个权重参数的梯度)
求误差E对w5的导数
![]()
导数(梯度)已经计算出来了,下面就是反向传播与参数更新过程
![]()
假如求w1,虽然比较复杂,但是思想是一样的
![]()
由于其强大的表示能力,BP神经网络经常遭遇过拟合,其训练误差持续降低,但测试误差却可能上升。有两种策略常用来缓解BP网络的过拟合,第一种策略是“早停”:将数据分为训练集和验证集,训练集用来计算梯度、更新连接权和阈值,验证集用来估计误差,若训练集误差降低但是验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阈值。第二种策略是“正则化”,其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分。
2.4 全局最小和局部极小
神经网络的训练过程可以看做一个参数寻优过程,即在参数过程中,寻找一组最优参数使得损失函数最小。
直观理解:局部极小值是参数空间中的某个点,其邻域点的损失函数值均不小于该点的函数值,全局最小解则是指参数空间中所有点的损失函数值均不小于该点的函数值。
我们在参数寻优股过程中希望找到的是全局最小。基于梯度的搜索使用最为广泛的参数寻优方法。
参考博客 “反向传播算法”过程及公式推导(超直观好懂的Backpropagation)_aift的博客-CSDN博客_反向传播算法
感知机原理小结 - 刘建平Pinard - 博客园