人工智能 - 遗传算法解决TSP(旅行商问题) Python实现
写在最前面
代码非原创!, 代码非原创!, 代码非原创!
代码主体部分来自于B站up主且有视频讲解,我在阅读之后觉得up写得不错,并在原代码的基础上用Echarts完善了最后数据可视化的部分。以下是我对该算法做的图文 + 注释导读,希望对看完视频还有不理解的同学有所帮助。
附上原视频 :【算法】遗传算法解决旅行商(TSP)问题_哔哩哔哩_bilibili
源代码的GitHub地址:https://github.com/zifeiyu0531/ga-tsp
为了更好的阅读,建议先去GitHub仓库clone源代码!!!
一.数据结构分析
为了更好的理解源代码,需对代码中使用到的两个类【individual】和【Ga】有一定的了解
1.individual类
源码如下:
class Individual:
def __init__(self, genes=None):
# 随机生成序列
if genes is None:
genes = [i for i in range(gene_len)]
random.shuffle(genes)
self.genes = genes
self.fitness = self.evaluate_fitness()
# 适应度即以当前序列走完一个闭合曲线的路径之和
def evaluate_fitness(self):
# 计算个体适应度
fitness = 0.0
for i in range(gene_len - 1):
# 起始城市和目标城市
from_idx = self.genes[i]
to_idx = self.genes[i + 1]
fitness += city_dist_mat[from_idx, to_idx]
# 连接首尾【最后一个城市->起点城市】
fitness += city_dist_mat[self.genes[-1], self.genes[0]]
return fitness
导读解析:
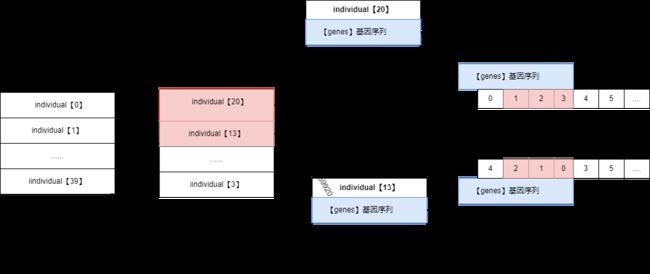
individual类:
代表了每一个迭代【Ga】中的【个体】
每个个体拥有如下【属性/特征】
· 【genes】基因序列: TSP中抽象为一次路线规划
· 【fitness】适应度 :TSP中抽象为按路线规划完一次的路径之和
每个个体拥有如下【方法/能力】
·【evaluate_fitness】计算适应度: 根据个体的genes计算其适应度
举例说明:
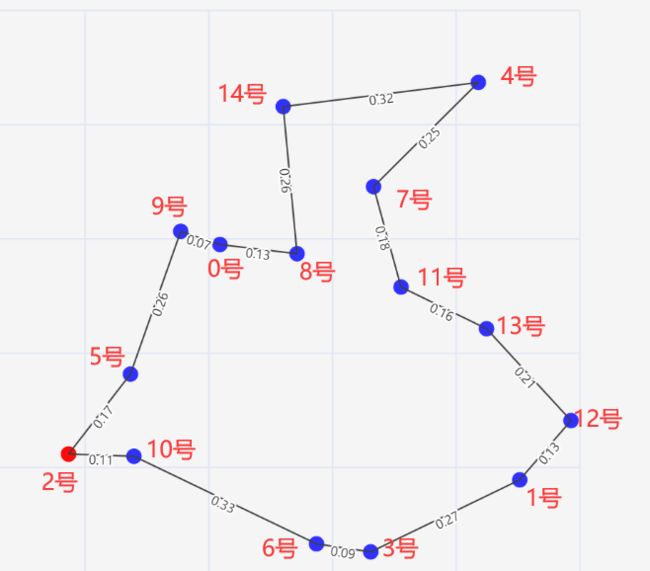
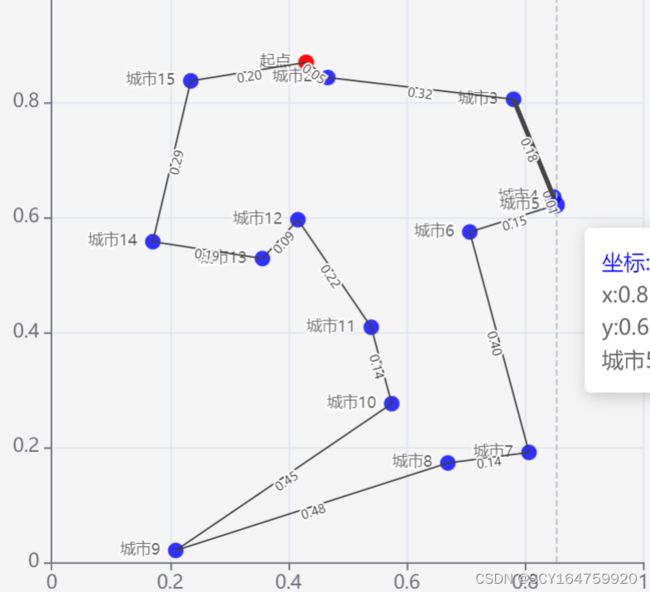
假设现有一个individual,其基因序列【genes】如下:
[2, 5, 9, 0, 8, 14, 4, 7, 11, 13, 12, 1, 3, 6, 10, 2]
其代表从 2号城市出发,依次经过 5号 , 9号,0 号城市..,最终返回一号城市
附上用Echarts绘制的图片便于理解
该个体的fitness即:按照【genes】序列走往图上一圈后,所有线段的距离之和,
具体到图例就是各连线上的【数值】之和:
fitness = 0.17 + 0.26 + 0.0.7 +0.13 + 0.26 + .... +0.11
2.Ga类
源码如下:
类中包含了实现遗传算法的算法具体实现,将在后文中详解,可先了解其
class Ga:
def __init__(self, input_):
global city_dist_mat
city_dist_mat = input_
self.best = None # 每一代的最佳个体
self.individual_list = [] # 每一代的个体列表
self.result_list = [] # 每一代对应的解
self.fitness_list = [] # 每一代对应的适应度
# 进行每代个体之间的交叉 返回生成的新基因list
def cross(self):
# 具体实现省略,后文给出
return new_gen
# 变异 用reverse来模拟变异
def mutate(self, new_gen):
# 具体实现省略, 后文给出
self.individual_list += new_gen
def select(self):
# 具体实现省略, 后文给出
self.individual_list = winners
@staticmethod
def rank(group):
# 冒泡排序 以fitness为依据
for i in range(1, len(group)):
for j in range(0, len(group) - i):
if group[j].fitness > group[j + 1].fitness:
group[j], group[j + 1] = group[j + 1], group[j]
return group
def next_gen(self):
# 交叉
new_gen = self.cross()
# 变异
self.mutate(new_gen)
# 选择
# 选择
self.select() # 有多种算法 轮盘赌 / 锦标赛
# 获得这一代留下的individual_list
for individual in self.individual_list:
# 遍历比较得到该代最好的individual
if individual.fitness < self.best.fitness:
self.best = individual
def train(self):
# 初代种群
self.individual_list = [Individual() for _ in range(individual_num)]
self.best = self.individual_list[0]
for i in range(gen_num):
self.next_gen()
result = copy_list(self.best.genes)
result.append(result[0])
self.result_list.append(result)
self.fitness_list.append(self.best.fitness)
return self.result_list, self.fitness_list, self.individual_list
导读解析:
Ga类
代表了每一次的种群迭代
每个迭代拥有如下【属性/特征】
- 【best】 每一代筛选出来的最优个体【best】
- 最优的判断标准为: 其fitness在该代中最小,即路径之和最短
- 【individual_list】 个体表 其中存放每次迭代过程中存货的个体[individual]
- 【result_list】 每一代筛选出来的最优个体【best】的genes序列将保存在该list中
- 【fitness_list】 每一代筛选出的最优个体【best】的fitness适应度将保存到该list中
每个迭代拥有如下【方法/能力】:
- 【cross】交叉遗传
- 【mutate】随机变异
- 【select】竞争存活
- 【rank】具体模拟”竞争“的算法
- 【next_gen】生成下一个迭代
- 即按一定顺序进行【cross】/【mutate】/【select】
- 【train】模拟整个遗传算法并生成最后结果
- 获取最终结果【result_list】+【fitness_list】
二.主要算法实现
1.cross 交叉遗传
先放图文解析,便于理解。
以某一次的交叉遗传为例
A.打乱individual_List,随机选择两个individual的随机长度的基因序列
假设此次选取了13号和20号个体【长度为3】,【起始位置为:1】的基因序列进行cross
B.错误的Cross
注意:
两个片段直接cross不是简单的交换序列,这样会导致一个individual中存在相同“城市DNA”的问题,如下图所示:
C.正确的Cross
正确的Cross:
两个待交换片段互相提供想要交换的城市DNA编码,然后在各自的DNA序列中进行交换。将原有的individual间的片段交换,转换为individual内片段的交换.
下面以一次实际交换为例进行分析:
D.算法实现
算法的核心是需要记录序列中每个DNA的位置,可采用字典进行记录,每次swap后动态更新字典,即可实现简单的Cross。
# 进行每代个体之间的交叉 返回生成的新基因list
def cross(self):
new_gen = []
# 打乱该代的个体列表
random.shuffle(self.individual_list)
# 选取相邻的两个个体进行交叉
for i in range(0, individual_num - 1, 2):
# 父代基因
genes1 = copy_list(self.individual_list[i].genes)
genes2 = copy_list(self.individual_list[i + 1].genes)
# 随机选择两个父代基因的截断位置进行交叉
# 交换的长度由index2-index1的长度决定
# index1需至少留下一个位置给index2 所以其random的取值为 len - 2
index1 = random.randint(0, gene_len - 2)
index2 = random.randint(index1, gene_len - 1)
# 得到parent基因的原序列字典
pos1_recorder = {value: idx for idx, value in enumerate(genes1)}
pos2_recorder = {value: idx for idx, value in enumerate(genes2)}
# (index1, index2 即为选出的待交换的片段)
for j in range(index1, index2):
# 取出parent基因j位置的值
value1, value2 = genes1[j], genes2[j]
# pos1查找母序列j位置的值在父序列的原位置
# pos2查找父序列j位置的值在母序列的原位置
pos1, pos2 = pos1_recorder[value2], pos2_recorder[value1]
# 根据pos和j交换单个序列模拟cross
genes1[j], genes1[pos1] = genes1[pos1], genes1[j]
genes2[j], genes2[pos2] = genes2[pos2], genes2[j]
# 更新插入数据字典
pos1_recorder[value1], pos1_recorder[value2] = pos1, j
pos2_recorder[value1], pos2_recorder[value2] = j, pos2
# 将生成的新基因append到list中
new_gen.append(Individual(genes1))
new_gen.append(Individual(genes2))
return new_gen
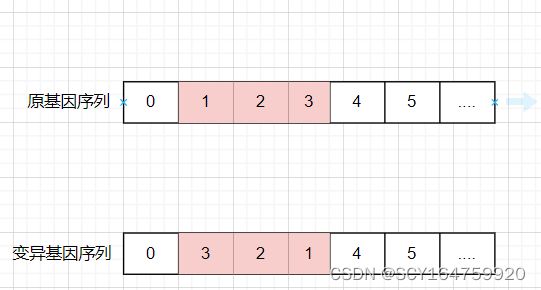
2.mutate 随机变异
变异的方法有很多种,源程序中选取的是【反转reverse基因片段】
即随机选取一定长度的基因片段,将该片段反转后替换原片段。
用下图举一个简单的例子:
源代码:
# 变异 用reverse来模拟变异
def mutate(self, new_gen):
# 从cross得到的新基因序列中遍历个体
for individual in new_gen:
# 根据生成的随机数与【变异概率相比较】
if random.random() < mutate_prob:
# 翻转切片
old_genes = copy_list(individual.genes)
# 随机选取进行mutate的基因片段
index1 = random.randint(0, gene_len - 2)
index2 = random.randint(index1, gene_len - 1)
# 截取基因片段
genes_mutate = old_genes[index1:index2]
# reverse基因片段
genes_mutate.reverse()
# 更新mutate后的individual的genes
individual.genes = old_genes[:index1] + genes_mutate + old_genes[index2:]
# 两代合并
self.individual_list += new_gen3.select 竞争
竞争的目的是筛选出每代保留下的个体,即生成新的individual_list。筛选的方法依据遗传算法的知识可知,有多种可以选择,例如:轮盘赌算法,锦标赛算法。
本次采用锦标赛算法,具体逻辑在这里就不多赘述了。直接贴上源码
def select(self):
# 锦标赛算法筛选此次迭代最终留下的individual
group_num = 10 # 小组数
group_size = 10 # 每小组人数
group_winner = individual_num // group_num # 每小组筛选出的individual【获胜者】
winners = [] # 锦标赛结果
for i in range(group_num):
group = []
for j in range(group_size):
# 随机组成小组
player = random.choice(self.individual_list) # 随机选择参赛者
player = Individual(player.genes) # 抽取参赛者的基因序列
group.append(player)
group = Ga.rank(group) # 对本次锦标赛获胜者按适应度排序
# 取出获胜者
winners += group[:group_winner]
self.individual_list = winners
@staticmethod
def rank(group):
# 冒泡排序 以fitness为依据
for i in range(1, len(group)):
for j in range(0, len(group) - i):
if group[j].fitness > group[j + 1].fitness:
group[j], group[j + 1] = group[j + 1], group[j]
return group4.next_gen 迭代
迭代的函数的作用: 将前面介绍的【cross】+【mutate】+【select】按一定的顺序执行,达到模拟一次遗传算法的过程,以一个流程图该函数的执行顺序.
A.流程图
B.源代码
def next_gen(self):
# 交叉
new_gen = self.cross()
# 变异
self.mutate(new_gen)
# 选择
# 选择
self.select() # 有多种算法 轮盘赌 / 锦标赛
# 获得这一代留下的individual_list
for individual in self.individual_list:
# 遍历比较得到该代最好的individual
if individual.fitness < self.best.fitness:
self.best = individual三.数据可视化
遗传算法执行完后,将得到【result_list】和【fitness_list】两个list,其内容分别为:
·【result_list】:每次迭代过程中保存的最优秀个体【best_genes】的集合,共40个
·【fitness_list】:【result_list】中每个【best_genes】对应的fitness集合,共40个
因此,现在要做的是将【result_list】中的最后一个元素取出作为【result】,因为该list中的最后一元素即最后一次迭代过程中【best_genes】,将其基因序列按坐标形式绘制并依次连接相邻两点,最终将得到路线图,我在up主源代码的基础上稍做了一些变动,既有Python原生实现的方法,也有Vue + Echarts实现的方案。
1.Python实现可视化
基于Python的matplotlib.pyplot库实现,使用前请先自行安装。
每次运行后,生成的图片将自动保存到【项目文件夹下】
只给出绘图部分的代码,替换github代码仓库中main.py中相对应的部分即可
# 绘图
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['KaiTi'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 根据结果绘图
fig = plt.figure()
x = result_pos_list[:, 0].copy().tolist()
y = result_pos_list[:, 1].copy().tolist()
np.savetxt("data.txt",result_pos_list)
# print("x轴", x)
# print("y轴", y)
# [:, 0]表示将二维数组的第一个下标全部取出并保存为一维数组 这里对应每个初始X轴的坐标
plt.plot(x, y, 'o-r',label="路线")
for a, b in zip(x, y): # 添加这个循环显示坐标
a = round(a, 3)
b = round(b, 3)
plt.text(a, b, (a, b), ha='center', va='bottom', fontsize=10)
plt.title(u"路线")
plt.legend()
fig.show()
plt.savefig("./route.png")
plt.clf()
fig = plt.figure()
plt.plot(fitness_list, label="适应度")
plt.title(u"适应度曲线")
plt.legend()
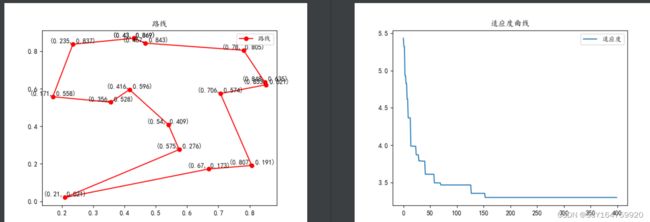
plt.savefig("./fitness.png")实现效果:
观察绘制结果可发现:根据图片不能确定哪一个是起点,也不知道两城市之间的路径长度,若你认为这个图片已经能满足你的需求,则不需要再阅读接下来的部分。
2.Vue2 + Echarts实现可视化
Echarts是一个不错的可视化工具,若有Vue基础的同学可自行尝试以下代码。
实现思路:
【前提】本次实验数据已被保存到了项目文件夹下的data.txt中
使用input框读取data.txt文件
对读取的数据内容进行处理,使其满足绘制Echarts图的要求
导入Echarts包,调用API完成绘图。
A.tempalte部分
B.script部分
C.css部分
D.实现效果: