GAN入门（1）-- 搭建一个简单的GAN网络-生成1010格式规律

        现在，我们来构建一个GAN，用生成器学习创建符合1010格式规律的值。这个任务比生成图像要简单。通过这个任务，我们可以了解GAN的基本代码框架，并实践如何观察训练进程。完成这个简单的任务有助于我们为接下来生成图像的任务做好准备。

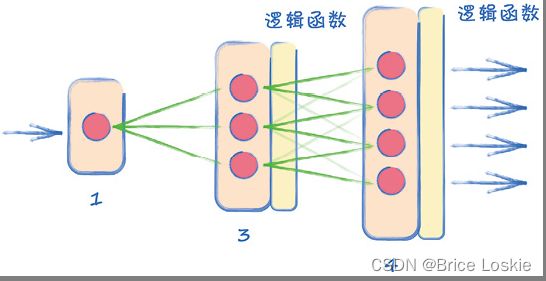
         我们看到的正是GAN的整体架构。真实的数据集被替换成了一个函数，会一直生成1010格式规律的数据。对于这样一个简单的数据源，我们不需要使用PyTorch的torch.utils.data.Dataset对象。生成器是一个神经网络，有4个输出值，我们希望训练它输出1010格式规律的数据。另一方面，鉴别器根据这4个值，试图判断它是来自真实数据源还是来自生成器。

        让我们依次对每个部分进行编码。启动一个新的笔记本，并导入标准库。

import torch 
import torch.nn as nn
import pandas as pd
import matplotlib.pyplot as plt
import random

        真实数据源可以是一个一直返回1010格式规律的数据的函数。

1.构建真实数据源

生成一个只返回1010的函数

def generate_real():
  real_data = torch.FloatTensor([1,0,1,0])
  return real_data

        不过，现实生活中很少有如此精确、恒定的数据。所以，让我们给高低值分别添加一些随机性，让这个函数更加真实。要生成随机数，我们需要导入Python的random模块，再使用random.uniform()函数。

def generate_real():
  real_data = torch.FloatTensor([random.uniform(0.8,1.0),
  random.uniform(0.0,0.2),
  random.uniform(0.8,1.0),
  random.uniform(0.0,0.2),
  ])
  return real_data

        测试一下这个函数，看它是不是能返回一个包含4个值的张量。其中，第1个和第3个值是0.8～1.0的随机数，第2和第4个值是0.0～0.2的随机数。

tensor([0.8858, 0.1156, 0.8412, 0.1627])

2.构建鉴别器

        我们先编辑鉴别器,它是一个继承自nn.Module的神经网络。我们按照PyTorch所需要的方式初始化网络，并创建一个forward()函数。

class Discriminator(nn.Module):
  def __init__(self):  
    super().__init__()
    self.model=nn.Sequential(
      nn.Linear(4,3),
      nn.Sigmoid(),
      nn.Linear(3,1),
      nn.Sigmoid()
    )
    self.loss_function=nn.MSELoss
    self.optmiser = torch.optim.SGD(self.parameter(),lr=0.01)
    self.counter=0
    self.progress=[]

        在以上代码中，我们通过nn.Sequential定义了网络层、一个均方误差损失函数以及一个随机梯度下降优化器。我们也创建了一个计数器（counter）和一个进程记录列表（progress），用于记录训练期间的损失变化。

        网络本身其实很简单。它在输入层有4个节点，因为输入是由4个值组成的。在最后一层，它输出单个值。该值为1表示为真，该值为0则表示为伪。隐藏的中间层有3个节点。它的确是一个非常小的网络!

        通过forward()函数调用上面的模型，输入数据并返回网络输出。

  def forward(self,inputs):
    return self.model(inputs)

训练函数train()

  def train(self,inputs,targets):
    #计算网络的输出
    outputs = self.forward(inputs)
    #计算网络的损失值
    loss = self.loss_function(outputs,targets)
    self.counter += 0
    if(self.counter % 10 == 0):
      self.progress.append(loss.item())
    if(self.counter % 1000==0):
      print("现在是第",self.counter+1,"次")
    self.optimiser.zero_grad()
    loss.backward()
    self.optimiser.step()

        损失值是通过比较输出值和目标值计算得到的。网络中的梯度由这个损失值计算得到，再通过优化器逐步更新可学习参数。我们通过计数器记录了train()函数被调用的次数，每调用10次添加损失值到列表中。

        最后，我们再创建一个plot_progress()函数，用来绘制损失值变化的图形。

  def progress(self):
    df=pd.DataFrame(self.progress,columns=['loss'])
    df.plot(ylim=(0,1.0),figsize=(16,8),alpha=0.1,marker='.',grid="True",ysticks=(0,0.25,0.5))

3. 测试鉴别器

        在任何机器学习架构中，对重要组件的测试都是很必要的。我们先来测试鉴别器。

        由于还没有创建生成器，因此我们无法真正测试与之竞争的鉴别器。目前能做的是，检验鉴别器是否能将真实数据与随机数据区分开。

        这听起来似乎没有什么用，不过它的确有效。它可以告诉我们，鉴别器至少有能力从随机数据中区分出真实数据。如果它做不到这一点，那么它也不太可能完成更艰巨的区分真实数据与看似真实的假数据的任务。所以，这个测试可以筛选出不太可能与生成器竞争的鉴别器。

        让我们创建一个函数来生成随机噪声。

        generate_random（4）会返回一个包含4个0～1的值的张量。读者可以自己试一下调整大小。

        现在让我们用一个训练循环来训练鉴别器，并对以下两种分类提供奖励：

        符合1010格式规律的数据是真实的, 目标输出为1.0；随机生成的数据是伪造的, 目标输出为0.0。

d=Discriminator()
for i in range(10000):
    d.train(generate_real(),torch.FloatTensor([1.0]))
    d.train(generate_random(4),torch.FloatTensor([0.0]))

d.plot_progress()

         训练循环会运行10 000次。鉴别器的train()函数接收来自generate_real()函数的真实数据，以及一个值为1.0的张量作为训练目标。这样做的目的是，鼓励网络对具有1010规律的实际数据尝试输出1.0。同样地，鉴别器的train()函数也会从generate_random()函数中接收随机噪声和目标值0.0，以鼓励它在看到不符合1010格式规律的数据时输出0.0。

        在一个新的单元格内运行训练循环。过程需要差不多10秒。完成之后，我们可以通过损失图了解训练效果。

        损失值先徘徊于0.25左右。之后，随着鉴别器从噪声中区分真实数据的表现越来越好，损失值下降至接近于0。

        在继续之前，让我们给训练后的鉴别器输入一些样本。如果我们的输入符合1010格式规律，我们应该得到一个接近1.0的值；如果我们的输入是随机生成的，输出应该接近0.0。

        让我们回顾一下到目前为止的进度。我们无法证明鉴别器可以与生成器有效地竞争。但能证明的是，鉴别器至少能学会从真实数据集和随机噪声中进行分辨。如果做不到这一点，我们就更不能指望它能与生成器竞争了。

4.构造生成器

        构建一个生成器需要花更多的工夫，让我们一步一步来进行。

        生成器是一个神经网络，而不是一个简单的函数，因为我们希望让它学习。我们希望它的输出能骗过鉴别器。这意味着输出层需要有4个节点，对应实际数据格式。

        生成器的隐藏层应该有多大? 输入层呢? 我们不需要局限于一个特定的大小，不过这个大小应该足以学习。但也不要太大，因为训练很大的网络需要花很长时间。同时，我们需要配合鉴别器的学习速度。因为我们不希望生成器和鉴别器中的任何一个领先另一个太多。基于这些考量，许多人从复制鉴别器的构造入手来设计生成器。

        它的输入层有1个节点，隐含层有3个节点，输出层有4个节点。这就是一个反向鉴别器。

         跟所有的神经网络一样，生成器也需要输入。生成器的输入应该是什么呢? 我们先从最简单的方案做起，即输入一个常数值。我们知道，太大的值会增加训练的难度，而标准化数据会有所帮助。我们暂时设输入值为0.5，如果遇到问题，可以回来修改。

        我们从定义一个生成器类Generator开始，可以直接复制鉴别器类Discriminator的代码并加以修改。

class Generator():
    def __init__(self):
        super().__init__()
        self.model=nn.Sequential(
            nn.Linear(1,3),
            nn.Sigmoid(),
            nn.Linear(3,4),
            nn.Sigmoid()
        )
        self.optimiser = torch.optim.SGD(self.parameter(),lr=0.01)
        self.counter=0
        self.progress=[]
    def forward(inputs):
        return self.model(inputs)

        从代码中可以看出，生成器类和鉴别器类的定义最明显的区别在于神经网络层的定义。

        读者可能已经发现，这里没有使用self.loss_function，因为我们不需要它了。回顾GAN的训练循环，我们使用的唯一的损失函数是根据鉴别器的输出计算的。最后，我们根据由鉴别器损失值计算的误差梯度来更新生成器。

        现在，让我们思考一下生成器的train()函数。生成器的训练与鉴别器的训练稍有不同。对于鉴别器，我们知道目标输出是什么。

        因此，训练生成器也需要鉴别器的损失值。实现这一关系的编码方法有多种。一种简单的方法是将鉴别器传递给生成器的train()函数。这样可以保持训练循环代码的整洁。

class Generator():
    def __init__(self):
        super().__init__()
        self.model=nn.Sequential(
            nn.Linear(1,3),
            nn.Sigmoid(),
            nn.Linear(3,4),
            nn.Sigmoid()
        )
        self.optimiser = torch.optim.SGD(self.parameter(),lr=0.01)
        self.counter=0
        self.progress=[]
    def forward(inputs):
        return self.model(inputs)
    def train(self,d,inputs,targets):
        g_output=self.forward(inputs)
        loss=d.loss_function(d_outputs,targets)
        self.counter+=1
        if(counter%10==0):
            self.progress.append(loss.item())
            pass
        self.optimiser.zero_grad()
        loss.backward()
        self.optimiser.step()
        pass
    pass

        这段代码很容易理解。首先，self.forward(inputs)将输入值inputs传递给生成器自身的神经网络。接着，通过D.forward(g_output)将生成器网络的输出g_ouput传递给鉴别器的神经网络，并输出分类结果d_output。鉴别器损失值由这个d_output和训练目标targets变量计算得出。误差梯度的反向传播由这个损失值触发，在计算图中经过鉴别器回到生成器。

        更新由self.optimiser而不是D.optimiser触发。这样一来，只有生成器的链接权重得到更新，这正是GAN训练循环第3步的目的。

        我们还删除了生成器里train()函数中的计数打印语句，改为在鉴别器的train()中打印。这样可以通过真实的训练数据更准确地反映训练进度。

        最后，我们在生成器类中加入plot_progress()函数

5.检查生成器输出

        同样地，我们推荐独立测试机器学习架构的每个组件是否正常工作。在训练生成器之前，让我们检查一下它的输出是否符合要求。

        在一个新的单元格中，运行以下代码来创建一个新的生成器对象，并输入一个值为0.5的单值张量。

        

g=Generator()
g.forward(torch.FloatTensor([0.5]))

tensor([0.4366, 0.6532, 0.6989, 0.2722], grad_fn=)

 6.训练GAN

%%time 

# create Discriminator and Generator

D = Discriminator()
G = Generator()

image_list = []

# train Discriminator and Generator

for i in range(10000):
    
    # train discriminator on true
    D.train(generate_real(), torch.FloatTensor([1.0]))
    
    # train discriminator on false
    # use detach() so gradients in G are not calculated
    D.train(G.forward(torch.FloatTensor([0.5])).detach(), torch.FloatTensor([0.0]))
    
    # train generator
    G.train(D, torch.FloatTensor([0.5]), torch.FloatTensor([1.0]))
    
    # add image to list every 1000
    if (i % 1000 == 0):
        image_list.append( G.forward(torch.FloatTensor([0.5])).detach().numpy() )

    pass

首先，我们创建了新的鉴别器和生成器对象。接着，运行训练循环10 000次。每次循环都重复训练GAN的3个步骤。

第1步，我们用真实的数据训练鉴别器。

第2步，我们使用一组生成数据来训练鉴别器。对于生成器输出，detach()的作用是将其从计算图中分离出来。通常，对鉴别器损失直接调用backwards()函数会计算整个计算图路径的所有误差梯度。这个路径从鉴别器损失开始，经过鉴别器本身，最后返回生成器。由于我们只希望训练鉴别器，因此不需要计算生成器的梯度。生成器的detach()可以在该点切断计算图。下图更直观地解释了这一点。

为什么要这么做呢？ 即使不这样做，照常计算生成器中的梯度，应该也不会有什么坏处吧? 的确，在我们这个简单的网络中，切断计算图的好处不是很明显。但是，对于更大的网络，这么做可以明显地节省计算成本。

第3步，我们输入鉴别器对象和单值0.5训练生成器。这里没有使用detach()，是因为我们希望误差梯度从鉴别器损失传回生成器。生成器的train()函数只更新生成器的链接权重，因此我们不需要防止鉴别器被更新。

接着，让我们使用 D.plot_progress() 函数看一下鉴别器的训练进展。

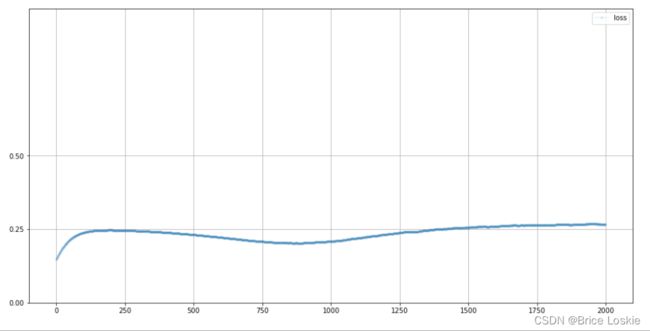
         在此之前，我们认为，随着神经网络在任务中的表现越来越好，我们的训练损失值将接近0。然而，这里的损失值保持在0.25左右。这个数字有什么特别的含义吗?

        当鉴别器不擅长从伪造数据中识别真实数据时，它就无法确定输出0.0还是1.0，索性就输出0.5。因为我们使用了均方误差，所以损失值的结果是0.5的平方，也就是0.25。

        在这里，随着训练的进行，损失值略有下降，但幅度并不大。这说明网络有了一些进步。目前还不清楚，它是在识别真实的1010格式规律方面做得更好，还是在识别生成的伪造数据方面做得更好，或者两方面都很出色。在训练的后期，损失值回升到0.25。这是一个好现象，说明生成器已经学会生成1010格式的数据，从而使鉴别器无法区分。换句话说，鉴别器的输出是0.5，介于0～1。这也正是损失值反弹到0.25的原因。

        让我们再通过G.plot_progress()了解一下生成器的训练进展。

         刚开始，鉴别器在区分真假模式时并不是很确定。在训练进行到一半时，损失值略有增加，这表明生成器在进步，开始可以骗过鉴别器了。在训练后期，我们看到生成器和鉴别器达到平衡。

        通过观察训练过程中的损失值变化来了解训练的进展是一个好习惯。从上面的两个图中，我们看到训练没有完全失败，也没有看到损失值的剧烈振荡，那是学习不稳定的一种表现。

        现在，让我们试验一下训练后的生成器，看看它会生成什么样的数据。这是我们第一次自己生成数据!

G.forward(torch.FloatTensor([0.5]))

tensor([0.9378, 0.0417, 0.9329, 0.0484], grad_fn=)

 我们可以看到，生成器的确输出了一个符合1010格式规律的结果，第1个和第3个值明显高于第2个和第4个值。高数值在0.9左右，低数值在0.05左右。效果相当不错。

        让我们增加一个额外的实验，看看1010格式规律在训练过程中是如何演变的。为此，我们可以在训练循环之前创建一个空列表image_list，每1 000次训练循环记录一次生成器的输出。

import numpy
plt.figure(figsize = (16,8))
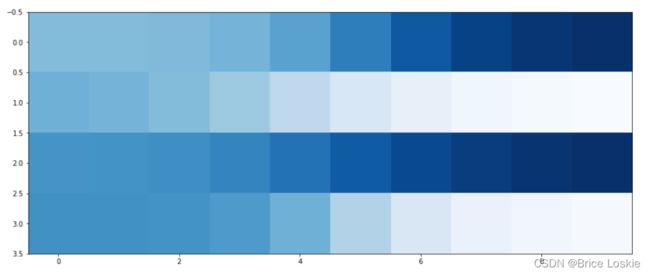
plt.imshow(numpy.array(image_list).T, interpolation='none', cmap='Blues')

         上图非常清楚地显示了生成器是如何随着训练时间而进步的。最初，生成器输出的规律相当模糊。在训练进行到一半时，生成器突然可以生成有点符合1010格式规律的图像了。在余下的训练过程中，该输出规律变得越来越清晰。