【深度学习】GAN生成对抗网络

GAN

论文解读

摘要简介

• 核心要点

1. 提出了一个基于对抗的新生成式模型，它由一个生成器和一个判别器组成
2. 生成器的目标是学习到样本的数据分布，从而能生成样本欺骗判别器;判别器的目标是判断输入样本是生成/真实的概率
3. GAN模型等同于博弈论中的二人零和博弈
4. 对于任意的生成器和判别器，都存在一个独特的全局最优解
5. 在本文中，生成器和判别器都由多层感知机实现，整个网络可以用反向传播算法来训练
6. 通过实验的定性与定量分析显示，GAN具备很大的潜力

• 提出了一种生成式的模型，通过对抗的过程来进行训练。生成式模型是要通过捕捉数据的分布进行训练从而生成数据，而判别式模型要通过对样本进行估计，区分出数据是由生成模型生成出来的还是真实样本里的，得到的是一个概率，概率越接近1，说明样本是真实的概率就越大。
• 生成器的训练目标是最大化判别器错误的概率，让判别器无法区别数据是来自哪里的；判别器的训练目标是尽可能地将样本数据区分出来。这个网络框架就是一个利用minimax算法来找到生成器和判别器的全局最优解。
• 这个全局最优解，生成器会覆盖整个训练数据的分布，判别器则是无论在哪判别的概率都是$\frac{1}{2}$.

研究背景

• 判别式模型

模型学习的是条件概率的分布$P(Y|X)$,也就是为了从属性$X$中预测出标记的类别$Y$
也就是在X发生的前提下，$Y$情况发生的概率

一般来说，判别式模型有其他几个模型，如：线性回归、逻辑回归、KNN、SVM、决策树、条件随机场、Boosting方法

• 生成式模型
  模型学习的是联合概率$P(x,y)$，为了得到属性为$X$且为$Y$类别时候的概率

生成式模型有：朴素贝叶斯、混合高斯模型、隐马尔可夫模型、贝叶斯网络、马尔可夫随机场、深度信念网络、变分自编码器

• 核心理论

  零和博弈：一方的收益必然导致另一方的损失，博弈各方的收益和损失相加总和为0，双方不存在合作。可以理解为零和博弈在意的不是结果，而是中间博弈的过程，在博弈的过程中不同的博弈过程会产生不同的结果。
  minimax：在零和博弈的基础上，为了使己方达到最优解，把目标设置为对方的利益最小化。

生成效果

研究意义

• 使AI具备了图像和视频的创作编辑能力
• 启发了无/弱监督学习的研究
• 应用方面有：图像生成、图像转换、图像编辑

介绍

在GAN中，作者是使用了通过对样本数据集添加随机的噪声生成生成样本数据，再输入到生成器里生成数据。论文作者是通过使用多层感知机来实现生成器和判别器模型，通过反向转播和Dropout算法来进行训练。

论文精读

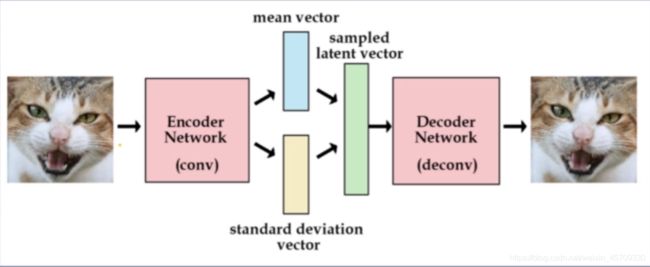
VAE(Variational Auto-Encoder)

VAE主要由三个部分组成

• 编码器
  把数据编码成mean vector 和 standard deviation vector
• 采样
  使用mean vector和standard deviation vector构建的高斯分布中采样得到Latent vector
• 解码器
  从Latent vector中生成数据
  

latent space，就是输入噪声的一个特征空间，也可以理解为一种有效的信息表示。有点像自编码器里的latent represention。
指隐变量$z$的样本空间。“隐变量”可以理解成控制数据$X$生成的“幕后之手”。在统计机器学习中，隐变量生成式模型“生成”数据$X$的背后逻辑是，通过建模联合分布$p_{\theta }(z,X)$ ，再从中采样得到$(z,X)$对。具体操作是，为隐变量选择一个容易采样的分布，如高斯，再通过神经网络建模$p_{\theta }(X|z)$，从而采样得到生成的数据。

使用的损失函数为:

• 对于生成loss

generation loss 是指生成的图片与真实图片之间的差差异程度

$$generation\_loss=mean(square(generated\_img-real\_img))$$

• 对于latent_loss

latent_loss 是指拟合出来的标准高斯分布的拟合程度，因此，我们可以使用KL散度对两个分布之间差异进行度量。KL散度越大，两个分布差别越大。反映的是拟合标准高斯分布的程度，拟合得越好，说明生成的数据更具有普遍性

$$latent\_loss=KL-Divergence(laten{t}_{v}ariable,uni{t}_{g}aussian)$$

• Loss
  $$loss=generatio{n}_{l}oss+laten{t}_{l}oss$$

GAN

• 生成器$G$
  由多层感知机、ReLU、Sigmoid组成

• 判别器$D$
  由多层感知机、Maxout、Dropout组成

价值函数

$$\underset{G}{\min }\underset{D}{\max }V(G,D)=E_{x-p_{data}(x)}[\log D(x)]+E_{z-p_z(z)}[\log (1-D(G(z)))]$$
对于价值函数的目标是
最大化$D$，也就是最大化$D(x)$和$1-D(G(z))$ 目的是为了能够让判别器更能够区分出来哪个是真实的数据，哪个是生成的数据。
对于$D$来说，目标函数可以写成
$$\underset{D}{\max }{E}_{x-p_r}[\log D(x)]+E_{x-p_g}[\log (1-D(x))]$$
其中，$D(x)$是判别模型的输出结果，输出的是一个概率，用来判断图片是真实图片的概率，$p_r$和$p_g$代表真实图像的分布与生成图像的数据分别情况，可以看出，为了能够使$D(x)$更大，就需要最大化判别模型的目标函数。

$E_{x-p_r}[\log D(x)]$是指使得真实数据放入到判别模型$D(x)$输出的计算值和整个式子的值尽可能大
$E_{x-p_g}[\log (1-D(x))]$是指使得造假数据放入到判别模型$D(x)$输出的计算值尽可能小和整个式子的值尽可能大，这样整合下来就会使得目标函数变大，因此在训练的过程中就可以根据目标函数进行梯度提升。（本质还是影响梯度）

对于$G$来说，目标函数为
$$\underset{G}{\min }\underset{D}{\max }{E}_{x-p_r}[\log D(x)]+E_{x-p_g}[\log (1-D(x))]$$
生成模型的目标是使得判别模型无法区分真实图片和生成图片，也就是要让式子尽量小。

训练流程

• 采用了mini-batch梯度下降
• 训练k次判别器
• 训练1次生成器

全局最优解

判别器的最优解
$$D_G^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$$
可以代入$x=0$和$x=1$
$x=0$时，判别器$D$为$1$，说明$x=0$这个数据是来自生成器的
$x=1$时，判别器$D$为$0$，说明$x=1$这个数据是来自真实数据的

生成器的最优解
$$p_g=p_{data}$$也就是生成数据的分布等于真实数据的分布
$$C^{\ast }=-\log (4)$$（价值函数的取值）

补充知识:
信息熵：描述一个概率分布的复杂程度（概率就已经可以看成事件发生了，所以可以用概率的分布描述信息熵，信息熵原本的定义是消除不确定性所需要的信息量，而不确定性事件就是指有一定概率发生的事件，所以描述一个事件的不确定性就可以用概率分布进行描述，而信息熵就是描述了一个为了确定这个不确定性事件所需要的信息量，信息量越大，说明事情的不确定性越大，也就是这件事情越复杂，所以信息熵就是描述一个概率分布的复杂程度的量）
概率分布再理解：概率的分布理解为一个事件是否发生的所有可能性，也就是描述了事件发生与否在数学上的描述。概率可以描述一个事情发生的可能性，概率的分布则是描述所有可能性在坐标轴上的分布。
KL散度：基于分布Q来描述分布P所需的额外信息量，也就是分布Q和分布P之间的差异性，P和Q差不多的非对称性的度量。两个分布之间的差距表示还需要多少的信息分布Q和分布P才可以相等
JS散度：基于KL散度，解决了KL散度的非对称问题。如果两个分布距离较远，没有重叠部分时，KL散度无意义，而JS散度为常数1

生成器的可收敛性

• 凸函数
  局部最优解等于全局最优解
• 上确界
  一个集合的最小上界，类似于最大值
• 次导数
  作一条直线通过点$(x,f(x))$，并且要么接触f，要么在f的下方，这条直线的斜率称为f的次导数
• 次梯度算法
  与梯度下降类似，用次梯度代替梯度，在凸函数上能确保收敛性。

模型优劣势

缺点

• 没有显式表示的$p_g(x)$
• 必须同步训练G和D，可能会发生模式崩溃

优点

• 不使用马尔科夫链，在学习过程中不需要推理
• 可以将多种函数合并到模型中
• 可以表示非常尖锐、甚至退化的分布
• 不是直接使用数据来计算loss更新生成器，而是使用判别器的梯度，所以数据不会直接复制到生成器的参数中

总结

GAN中相互影响的部分是由于判别器是梯度上升，生成器是梯度下降，用判别器的梯度更新生成器

关键点

• 对抗性框架设计
• 价值函数设计
• 全局最优解求解
• GAN的改进方向

创新点

• 使用神经网络来判别两个分布的相似程度
• 把两个相互对抗的loss作为唯一的优化目标

启发

• 从生物智能中挖掘宝藏——博弈与竞争
• 对抗在机器学习的应用，更多的对抗方式
• 深度神经网络可以解决99%的问题
• 评价两个分布的相似性是一个重难点
• 能否结合统计学方法与DL方法的优缺点