机器学习(二)---朴素贝叶斯算法
机器学习(二)—朴素贝叶斯算法
一、 贝叶斯定理
1、准备知识
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。
这个定理解决了现实生活里经常遇到的问题:已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:。
1、条件概率公式
条件概率是指在事件 Y=yY=y 已经发生的条件下,事件 X=xX=x 发生的概率。条件概率可表示为: P(X=x|Y=y)P(X=x|Y=y) 。而条件概率计算公式为:
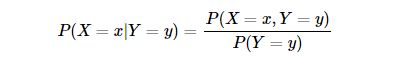
其中 P(X=x,Y=y)P(X=x,Y=y) 是联合概率,也就是两个事件共同发生的概率。而 P(Y=y)以及P(X=x)P(Y=y)以及P(X=x) 是先验概率。
我们用例子来说明一下就是: “某公园男性穿凉鞋的概率为 1212 ”,也就是说“是男性的前提下,穿凉鞋的概率是 1212 ”,此概率为条件概率,即 P(X=x1|Y=ymen)=12P(X=x1|Y=ymen)=12 。同理“女性穿凉鞋的概率为 2323 ” 为条件概率 P(X=x1|Y=ywomen)=12P(X=x1|Y=ywomen)=12 。
2、全概率公式
全概率公式是指:如果事件 Y=y1,Y=y2,…,Y=ynY=y1,Y=y2,…,Y=yn 可构成一个完备事件组,即它们两两互不相容,其和为全集。则对于事件 X=xX=x 有:
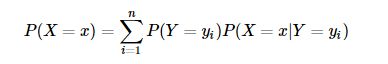
因此对于上面的例子,我们可以根据全概率公式求得:
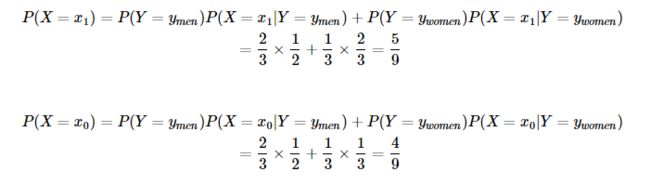
也就是说不考虑性别的情况下,公园中穿脱鞋的概率为56% ,不穿拖鞋的概率为 44% 。
二、代码实现
# coding=utf-8
from numpy import *
#过滤网站的恶意留言 侮辱性:1 非侮辱性:0
#创建一个实验样本
def loadDataSet():
postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1]
return postingList , classVec
#创建一个包含在所有文档中出现的不重复词的列表
def createVocalList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document) #????????
return list(vocabSet)
#将文档词条转换成词向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
#朴素贝叶斯分类器训练函数,从词向量计算概率
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords) #避免一个概率值为0,最后的乘积也为0
p1Num = ones(numWords) #用来统计两类数据中,各词的词频
p0Denom = 2.0 #用于统计0类中的总数
p1Denom = 2.0 #用于统计1类中的总数
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num / p1Denom) # 在类1中,每个次的发生概率
p0Vect = log(p0Num / p0Denom) # 避免下溢出或者浮点数舍入导致的错误 下溢出是由太多很小的数相乘得到的
return p0Vect, p1Vect, pAbusive