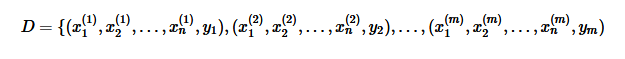机器学习（1）-贝叶斯（朴素贝叶斯，贝叶斯网络）

                                             贝叶斯算法

由于小组内项目需要，出于技术储备，小组每个人学习一个机器学习算法，做成ppt，然后给出训练数据，用python写出代码，并运行看效果，我抽到的是贝叶斯算法，大学的时候学习过，整个组都讲完了，是时候整理一下了～

贝叶斯算法基本概念：

贝叶斯分类算法是统计学的一种分类方法，它是一类利用概率统计知识进行分类的算法。在许多场合，朴素贝叶斯(Naïve Bayes，NB)分类算法可以与决策树和神经网络分类算法相媲美，该算法能运用到大型数据库中，而且方法简单、分类准确率高、速度快。 由于贝叶斯定理假设一个属性值对给定类的影响独立于其它属性的值，而此假设在实际情况中经常是不成立的，因此其分类准确率可能会下降。为此，就衍生出许多降低独立性假设的贝叶斯分类算法，如TAN(tree augmented Bayes network)算法。

有这么一个题目：

先验概率：

假设某公园中一个人是男性为事件 Y=men ,是女性则是 Y=women ；一个人穿凉鞋为事件 X=x1 ，未穿凉鞋为事件 X=x0 。而一个人的性别与是否穿凉鞋这两个事件之间是相互独立的。于是我们可以看到该例子中存在四个先验概率： 

                                                                    P(X=x1)与P(X=x0)                            

                                                              P(Y=ymen)与P(Y=ywomen)

其中 P(Y=ymen)与P(Y=ywomen) 可以根据例子中“该公园中男女比例通常为 2:1 ” 这一以往经验求得：P(Y=ymen)=2/3 以及 P(Y=ywomen)=1/3 。而先验概率 P(X=x1)与P(X=x0) 并不能直接得出，需要根据全概率公式来求解。在学习全概率公式之前，我们先了解一下条件概率。

条件概率：

条件概率是指在事件 Y=y 已经发生的条件下，事件 X=x 发生的概率。条件概率可表示为： P(X=x|Y=y) 。而条件概率计算公式为：                 

                                                          P(X=x|Y=y)=P(X=x,Y=y)/P(Y=y)

其中 P(X=x,Y=y) 是联合概率，也就是两个事件共同发生的概率。而 P(Y=y)以及P(X=x) 是先验概率。

我们用例子来说明一下就是： “某公园男性穿凉鞋的概率为 1/2 ”，也就是说“是男性的前提下，穿凉鞋的概率是 1/2 ”，此概率为条件概率，即 :

                                                             P(X=x1|Y=ymen)=1/2 。

同理“女性穿凉鞋的概率为 2/3 ” 为条件概率 

                                                            P(X=x1|Y=ywomen)=2/3 。

全概率公式:

全概率公式是指：如果事件 Y=y1,Y=y2,...,Y=yn 可构成一个完备事件组，即它们两两互不相容，其和为全集。则对于事件 X=x 有：                                 

                                            

因此对于上面的例子，我们可以根据全概率公式求得：

                    P(X=x1)=P(Y=ymen)P(X=x1|Y=ymen)+P(Y=ywomen)P(X=x1|Y=ywomen)=2/3×1/2+1/3×2/3=5/9

                    P(X=x0)=P(Y=ymen)P(X=x0|Y=ymen)+P(Y=ywomen)P(X=x0|Y=ywomen)=2/3×1/2+1/3×1/3=4/9

也就是说不考虑性别的情况下，公园中穿拖鞋的概率为 5/9 ，不穿拖鞋的概率为 4/9

后验概率:

后验概率是指，某事件 X=x 已经发生，那么该事件是因为事件 Y=y 的而发生的概率。也就是上例中所需要求解的“在知道一个人穿拖鞋的前提下，这个人是男性的概率或者是女性的概率是多少”。后验概率形式化便是：

                                                                    P(Y=ymen|X=x1)

后验概率的计算要以先验概率为基础。后验概率可以根据通过贝叶斯公式，用先验概率和全概率计算出来。

贝叶斯公式：

                                         P(Y=yman|X=x1) = P(X=x1|Y=ymen)*P(Y=ymen)/P(X=x1)

推导过程：

                                               P(Y=yman|X=x1)  = P(Y=yman,X=x1)/P(X=x1)

                                             P(X=x1|Y=yman)  = P(Y=yman,X=x1)/P(Y=yman)

两式可得：

                                       P(Y=yman|X=x1)*P(X=x1) =P(X=x1|Y=yman)*P(Y=yman)

即证明：                        P(Y=yman|X=x1) = P(X=x1|Y=ymen)*P(Y=ymen)/P(X=x1)

以上问题的计算公式如下：           

                                        

而朴素贝叶斯算法正是利用以上信息求解后验概率，并依据后验概率的值来进行分类。  使用上面的例子来进行理解，后验概率为：

                       

                       

也就是说，在知道一个人穿拖鞋的前提下，这个人是男性的概率是 3/5 ,是女性的概率是 2/5 。如果问题是“判断该人是男性还是女性”，此问题就是一个分类问题。由于依据贝叶斯公式计算的后验概率是男性的概率大于是女性的概率，即由于 P(Y=ymen|X=x1)>P(Y=ywomen|X=x1) ，那么我们就可以将其分类为男性（实际在使用朴素贝叶斯进行分类时，不需要求解分母 P(X=x1) ）。到此，我们已经使用例子来讲解了使用朴素贝叶斯进行分类的基本步骤以及简单的原理了。接下来我们将对朴素贝叶斯的原理进行详细地探讨。

朴素贝叶斯的推导

                      

其中 m 表示有 m 个样本， n 表示有 n 个特征。 yi,i=1,2,..,m 表示样本类别，取值为 {C1,C2,...,CK} 

先验概率：P(Y=Ck),k=1,2,...,K

条件概率为（依据条件独立假设）：

                

则后验概率为：

                   

上式为朴素贝叶斯分类的基本公式。于是，朴素贝叶斯分类器可表示为：

                      

由于分母对所有的 Ck 都是相同的，所以： 

                       

问题引出：

但是在实际问题中并不都是这样幸运的，我们能获得的数据可能只有有限数目的样本数据，而先验概率p(wi)和类条件概率p(x|wi)(各类的总体分布)都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。先验概率的估计较简单，1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计。类条件概率的估计（非常难），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度p(x|wi)转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了。

解决方法：极大似然

这是我从百度找了极大似然估计的一个例子

具体使用：

假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？我想很多人立马有答案：70%。这个答案是正确的。可是为什么呢？（常识嘛！这还要问？！）其实，在很多常识的背后，都有相应的理论支持。在上面的问题中，就有最大似然法的支持        我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜色服从同一独立分布。这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的概率是P(Data | M)，这里Data是所有的数据，M是所给出的模型，表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1，第二抽样的结果记为x2，。。。那么Data = (x1,x2,...,x100)。这样， P(Data | M) = P(x1,x2,...,x100|M) = P(x1|M)P(x2|M)...P(x100|M) = p^70(1-p)^30.

那么p在取什么值的时候，P(Data |M)的值最大呢？将p^70(1-p)^30对p求导，并其等于零。 70p^69(1-p)^30-p^70*30(1-p)^29=0。 解方程可以得到p=0.7。

朴素贝叶斯算法过程：

以参数估计为极大似然估计为例： 样本集为：

                             

其中 yi,i=1,2,..,m 表示样本类别，取值为 {C1,C2,...,CK} 。      

（1）计算先验概率：求出样本类别的个数 K 。对于每一个样本 Y=Ck ，计算出 P(Y=Ck) 。其为类别 Ck 在总样本集中的频率。 （2）计算条件概率：将样本集划分成 K 个子样本集，分别对属于 Ck 的子样本集进行计算，计算出其中特征 Xj=aj 的概率： P(Xj=ajl|Y=Ck)。其为该子集中特征取值为 ajl 的样本数与该子集样本数的比值。                                                                         （3）针对待预测样本 xtest ，计算其对于每个类别 Ck 的后验概率：

                                  

概率值最大的类别即为待预测样本的预测类别。   

朴素贝叶斯算法分析：

优点：

（1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。                                                                                                 （2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。                                                                                                                                                                                             （3）对缺失数据不太敏感，算法也比较简单，常用于文本分类

缺点：       

（1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。                                                                                                                                                                     （2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。                                                                                                                                                             （3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。                                    （4）对输入数据的表达形式很敏感。

问题：

    类条件独立性假设——朴素贝叶斯分类基于类条件独立性假设成立，而大多数情况下类条件独立性假设不成立，从而导致误差较大，无法使用朴素贝叶斯分类。

解决：贝叶斯网络 

贝叶斯网络（Bayesian network），又称信念网络（belief network）或是有向无环图模型（directed acyclic graphical model），是一种概率图型模型。  贝叶斯网络又称信度网络，是Bayes方法的扩展，是目前不确定知识表达和推理领域最有效的理论模型之一。从1988年由Pearl提出后，已经成为近几年来研究的热点.。一个贝叶斯网络是一个有向无环图(Directed Acyclic Graph,DAG),由代表变量节点及连接这些节点有向边构成。节点代表随机变量，节点间的有向边代表了节点间的互相关系(由父节点指向其子节点)，用条件概率进行表达关系强度，没有父节点的用先验概率进行信息表达。节点变量可以是任何问题的抽象，如：测试值，观测现象，意见征询等。适用于表达和分析不确定性和概率性的事件，应用于有条件地依赖多种控制因素的决策，可以从不完全、不精确或不确定的知识或信息中做出推理。

数学定义：

令G= (I,E) 表示一个有向无环图（DAG），其中I代表图中所有的节点的集合，而E代表有向连接线段的集合，且令X= (Xi)i∈I为其有向无环图中的某一节点i所代表之随机变量，若节点X的联合概率分布可以表示成：

                                                                             

则称 X 为相对于一有向无环图 G 的贝叶斯网络，其中pa(i)表示节点 i 之“因”。 对任意的随机变量，其联合分布可由各自的局部条件概率分布相乘而得出：

                                              

依照上式，我们可以将一贝叶斯网络的联合概率分布写成： 

                                    

上面两个表示式之差别在于条件概率的部分，在贝叶斯网络中，若已知其“因”变量下，某些节点会与其“因”变量条件独立，只有与“因”变量有关的节点才会有条件概率的存在。

贝叶斯网络通过一个有向无环图来表示一组随机变量跟它们的条件依赖关系。它通过条件概率分布来参数化。每一个结点都通过P(node|Pa(node))来参数化，Pa(node)表示网络中的父节点。它允许在变量的子集间定义类条件独立性，他提供一种因果关系图形模型，可以在其上进行学习。

                                                                    

一个简单的贝叶斯网络，其对应的全概率公式为：    

                                                                 P(a,b,c)=P(c∣a,b)P(b∣a)P(a)

 

                                                               

较复杂的贝叶斯网络，其对应的全概率公式为：

                       P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)

贝叶斯网络的第一种结构形式如下图：

head-to-head

                                                                       

P(a,b,c) = P(a)*P(b)*P(c|a,b)成立，化简后可得：

                                                              

在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立。

tail-to-tail

                                                                 

考虑c未知，跟c已知这两种情况： 

 在c未知的时候，有：P(a,b,c)=P(c)*P(a|c)*P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。 在c已知的时候，有：P(a,b|c)=P(a,b,c)/P(c)，然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知时，a、b独立。所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为tail-to-tail条件独立 。

head-to-tail

贝叶斯网络的第三种结构形式如下图：

                                                                   

还是分c未知跟c已知这两种情况： c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。 c已知时，有：P(a,b|c)=P(a,b,c)/P(c)，且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c)，可化简得到：

                                                                

在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。

 head-to-tail

                                                                         
xi+1的分布状态只和xi有关，和其他变量条件独立。通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）
                                                          

贝叶斯的应用：

医学检验：      

假设人类患某种癌症的概率是0.08%（即平均1万人有8人患这种癌症），现在最先进的技术检测患这种癌的正确率是99%（患癌检测准确概率99%，不患癌检测准确概率也是99%），如果小明检测患这种癌，那么他患这种癌症的概率是多少？      

仅凭直觉判断的话，正确率是99%嘛，那么患癌的概率就是99%，那么可以准备化疗，或者等死了。但是条件概率告诉我们不是这样。  假设A表示小明患癌，B表示检测患癌，那么我们要知道的是P(A|B)，而不是P(B)。根据贝叶斯公式：P(A|B)=[P(B|A)*P(A)]/P(B) P(B|A)表示患癌的前提下，检测患癌的概率，99% P(A)表示小明患癌的概率0.08% P(B)表示随机一个人被检测患癌的概率，根据全概率公式，有两种可能：患癌被检测患癌+没患癌被检测患癌=0.08%*99%+99.92%*1% 带入上面的公式P(A|B)=7.34%。 如果需要确诊，可以再检测一次，检测正确率就变成了99.99%，带入上面的公式： P(A|B)=88.9%   1% * 1% = 0.01%

小结：

朴素贝叶斯：       

简单，易理解，使用有效，排除了噪声与无关变量的影响（类条件独立性假设）。 

贝叶斯网络：      

放宽了变量无关的假设，便于解决复杂的不确定性和关联性问题