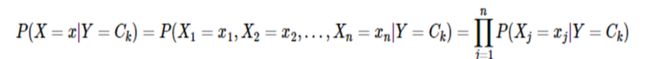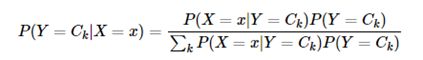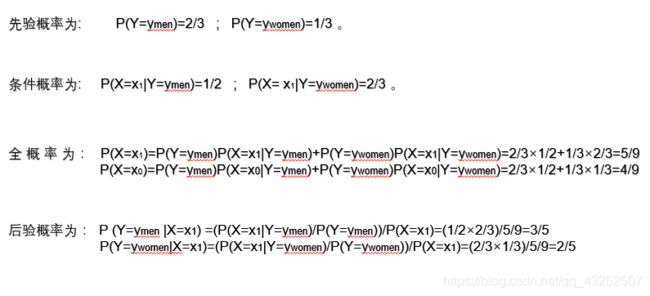数据挖掘十大算法---朴素贝叶斯
一、介绍
朴素贝叶斯:基于贝叶斯定理与特征条件独立假设的分类方法
优点:原理和实现都比较简单;
对小规模的数据表现很好,能处理多分类任务;
对缺失数据不太敏感,常用与文本分类。
缺点: 假设属性之间相互独立,这个假设在实际应用中往往是不成立的;
在属性个数比较多或者属性之间相关性较大时,分类效果不好。
二、概念解释
先验概率:根据以往经验和分析得到的概率。 记为:P(Y = Ci), i = 1, 2, 3, ….K
联合概率:指在多元的概率分布中多个随机变量分别满足各自条件的概率。记为:P(Xi, Yi)
条件概率:在事件 Y=y 已经发生的条件下,事件 X=x 发生的概率。记为:P(X = x | Y = y)
后验概率:某事件 X=x 已经发生,那么该事件是因为事件 Y=y 的而发生的概率。记为:P(Y = y | X = x)
全 概 率:如果事件X1、X2、X3…Xn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Xi)大于0,则对任一事 件Y有 P(Y)=P(Y|X1)P(X1) + P(Y|X2)P(X2) + ... + P(Y|Xn)P(Xn)。
三、相关公式
全 概 率
后验概率
四、实例计算
在夏季,某公园男性穿凉鞋的概率为 1/2 ,女性穿凉鞋的概率为 2/3 ,并且该公园中男女比例通常为 2:1
问题:若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
五、实现---文本分类
import numpy as np
import re
# 下载数据
'''
每个文本文件都是开头为类别信息,之后为文本内容
步骤:
(根据具体数据的形式变动)
1、导入
2、创建两个列表,document为存放每个文本文件,classes存放每个文本的类别信息
3、对导入的文件循环,对文件中的每一行进行空格切分,切分后的结果分别存放到两个列表中返回。
伪代码:
f = open('')
document = []
classes = []
for line in f.readlines():
lineArr = line.strip().split()
classes.append(lineArr[0])
document.append(lineArr[1:])
'''
def loadDataSet():
f = open('testSet.txt')
texts = []
classes = []
for line in f.readlines():
lineArr = line.strip().split()
classes.append(int(lineArr[0]))
texts.append(lineArr[1:])
return texts, classes
# 创建单词表
'''
目的:用于后期将文本中的每个句子转换为向量表示
伪代码:
vocaList = set([])
for i in texts:
vocaList = vocaList | set(i) # 求并集
'''
def getVocaList(texts):
vocaList = set([])
for i in texts:
vocaList = vocaList | set(i)
return list(vocaList) # 转换为列表形式,因为set类型没有索引对象,功能不多
# 将文本转换为向量
'''
目的:计算机可以识别进行运算的语言
注意:1、每个文本中的句子长度不一致问题(得到的向量长度不一致)
伪代码:
textVec = [0] * len(vocaList) * 初始化文本向量(我们用到的数据每个文本只包含一个句子,每个文本向量就是一个句子组成的一维向量
for word in text:
if word 在 单词表中:
该单词在单词表中的位置 映射到 文本向量中对应的位置 该位置置为1
else:
跳过(主要用于测试样本中,如果出现没有遇见过的单词)
'''
def getTextVec(vocaList, text):
textVec = [0] * len(vocaList)
for word in text:
if word in vocaList:
textVec[vocaList.index(word)] = 1
else:
pass
return textVec
# 生成训练矩阵
'''
目的:将每个文本转换为向量表示,形成训练矩阵,方便计算各种概率
'''
def getTrainMatrix(vocaList, texts):
trainMatrix = []
for text in texts:
textVec = getTextVec(vocaList, text)
trainMatrix.append(textVec)
return trainMatrix
# 计算所需要的各种概率
'''
目的:基于训练样本,计算先验概率、条件概率,用于测试样本的后验概率计算
伪代码:
textsNum = 训练样本的个数
wordsNum = 样本特征数,其实也就是单词表的大小。特征在这里就是单词表中的每个单词
pAbusive = 1类样本个数/总样本个数,p(y=1)先验概率
p0num = np.ones(wordsNum) # 初始化向量, 用于存放0类的样本中,单词j出现的次数(注意这个代码中没有考虑词频,如果样本中【有】该单词就为1)
p1num = np.ones(wordsNum) # 同上,1类。单词表中的每个单词在每一类都有存在的可能性,但是不一定在训练样本中有所体现,使用拉普拉斯平滑,避免0概率
p0Denom = p1Denom = 2.0 # 表示0类1类样本的总词数(拉普拉斯平滑) # (nc + mp)/ (n + p),mp =1, 等价样本数量为2,p = 1/2
for i in range(len(textsNum)):
if 第i个类别为1:
累计为1类中每个单词出现的词数 p1Num
累计为1类中出现单词总数 p1Denom
else: (0类)
(同上)
p1CondProb = np.log(p1Num / p1Denom) # 得到的结果是向量形式(p(x0=1|y=1),p(x1=1|y=1),...p(xn=1|y=1))
p0CondProb = np.log(p0Num / p0Denom ) # 取对数,方便计算,条件概率
'''
def trainNB(trainMatrix, trainClasses):
textsNum = len(trainMatrix)
wordsNum = len(trainMatrix[0])
pAbusive = sum(trainClasses) / float(textsNum)
p0Num = np.ones(wordsNum)
p1Num = np.ones(wordsNum)
p1Denom = p0Denom = 2.0
for i in range(textsNum):
if trainClasses[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
p1CondProb = np.log(p1Num / p1Denom)
p0CondProb = np.log(p0Num / p0Denom)
return p0CondProb, p1CondProb, pAbusive
# 测试集分类
def classifyNB(vocaList, test,p0CondProb, p1CondProb,pAbusive):
testArr = re.findall(r'[a-zA-Z0-9]+',test)
testVec = np.array(getTextVec(vocaList,testArr))
p1Prob = sum(testVec * p1CondProb) + np.log(pAbusive)
p0Prob = sum(testVec * p0CondProb) + np.log(1 - pAbusive)
if p1Prob > p0Prob:
return 1
else:
return 0
def testingNB():
texts,labels = loadDataSet()
vocaList = getVocaList(texts)
trainMatrix = getTrainMatrix(vocaList, texts)
p0P, p1P, pA = trainNB(trainMatrix,labels)
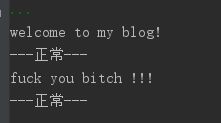
testSet = ['welcome to my blog!',
'fuck you bitch !!!']
for test in testSet:
print(test)
if classifyNB(vocaList,test, p0P, p1P, pA):
print('---垃圾---')
else:
print('---正常---')
testingNB()