Siamese 目标跟踪:Rotation Equivariant Siamese Networks for Tracking(CVPR2021)
论文 Rotation Equivariant Siamese Networks for Tracking
参考文章1 Rotation Equivariant Siamese Networks for Tracking
参考文章2 [论文阅读 2021 CVPR 目标跟踪]Rotation Equivariant Siamese Networks for Tracking
1.Motivation
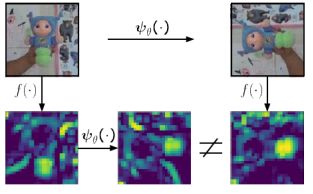
本文重点是处理目标的平面旋转对Siamese跟踪器性能的不利影响。在没有采取有效解决方案的情况下,目标旋转被认为是最困难的跟踪挑战。
- 基于深度学习的跟踪算法中使用了CNN,虽然CNN具有平移不变性,但是没有解决旋转问题。视频中存在旋转目标时,现有的跟踪器会受到严重影响。
- 一般情况下训练模型的时候,会使用图像增广让网络学习何种旋转角度的物体特征,通过对原图进行随机的仿射变换生成更多的训练样本以提高模型的鲁棒性。这篇论文认为采用图像增广的方式让模型学习旋转物体的特征有一些不足。训练数据和计算量大;旋转角度灵活,网络难学习到;当目标被相似物体包围时,更难区分相似物体。
2.Contribution
- RE-SiamNet:将旋转等变性(rotation equivariance)引入现有Siamese跟踪中,使跟踪器从一开始就捕获旋转变化,不需要额外的数据扩充。Rotation equivariant networks在图像分类、边缘检测、图像分割等领域中有广泛研究的应用。
- 引入附加的运动约束改善视频中的时间对应性。
- 新数据集:旋转目标基准(ROB),专用于平面内旋转的序列。
3.Network
(1)Equivariance(等变性)
等变性:要求函数与对称组在其域和共域上作用相同。
f ( ψ g Y ( x ) ) = ψ g Y ( f ( x ) ) g ∈ G , x ∈ X , 等 式 1 f\left( {\psi _g^Y(x)} \right) = \psi _g^Y(f(x)){\rm{ }}g \in G,x \in X {,等式1} f(ψgY(x))=ψgY(f(x))g∈G,x∈X,等式1
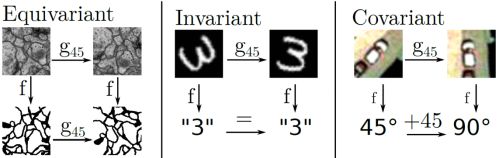
e q u i v a r i a n c e : f ( g ( ⋅ ) ) = g ( f ( ⋅ ) ) equivariance:f(g( \cdot )) = g(f( \cdot )) equivariance:f(g(⋅))=g(f(⋅))
i n v a r i a n c e : f ( g ( ⋅ ) ) = f ( ⋅ ) invariance:f(g( \cdot )) = f( \cdot ) invariance:f(g(⋅))=f(⋅)
c o v a r i a n c e : f ( g ( ⋅ ) ) = g ′ ( f ( ⋅ ) ) covariance:f(g(\cdot ))={{g}^{\prime }}(f(\cdot )) covariance:f(g(⋅))=g′(f(⋅))
(2)Rotation equivariance(旋转等变性)
CNN可以通过可控滤波器(steerable filters)加强旋转等变性。可控滤波器CNN(SFCNN)将权重共享的概念从平移( translation group)扩展到旋转。对于具有可控滤波器的旋转等变性,网络必须对每个滤波器的不同旋转版本进行卷积。在这种情况下,权重共享有助于模型更好的泛化。
可控滤波器:
ψ j k ( r , ϕ ) = τ j ( r ) e i k ϕ , 等 式 2 {\psi _{jk}}(r,\phi ) = {\tau _j}(r){e^{{\text{i}}k\phi }} {,等式2} ψjk(r,ϕ)=τj(r)eikϕ,等式2其中, ϕ ∈ ( π , π ] \phi \in (\pi ,\pi ] ϕ∈(π,π]和 j = 1 , 2 , … , J j = 1,2, \ldots ,J j=1,2,…,J,允许控制基函数的径向部分。 ( r , ϕ ) \left( {r,\phi } \right) (r,ϕ)表示 ( x 1 , x 2 ) ({x_1},{x_2}) (x1,x2)在极坐标中的变化形式, k ∈ Z k \in \mathbb{Z} k∈Z表示角频率。
Circular harmonics可以将 ψ j k {\psi _{jk}} ψjk上的旋转表示为具有复指数的乘法:
ρ θ ψ j k ( x ) = e − i k θ ψ j k ( x ) , 等 式 3 {\rho _\theta }{\psi _{jk}}(x) = {e^{ - {\text{i}}k\theta }}{\psi _{jk}}(x) {,等式3} ρθψjk(x)=e−ikθψjk(x),等式3其中,为清楚起见, ψ j k ( ⋅ ) {\psi _{jk}}\left( \cdot\right) ψjk(⋅)表示为 ψ j k ( x ) {\psi _{jk}}\left( x\right) ψjk(x)。
然后,将每个学习到的滤波器构建为基本滤波器的线性组合:
Ψ ( x ) = ∑ j = 1 J ∑ k = 0 K w j k ψ j k ( x ) , 等 式 4 \Psi (x) = \sum\limits_{j = 1}^J {\sum\limits_{k = 0}^K {{w_{jk}}} } {\psi _{jk}}(x){,等式4} Ψ(x)=j=1∑Jk=0∑Kwjkψjk(x),等式4其中, ψ j k ∈ C {\psi _{jk}} \in C ψjk∈C为权重。
要旋转 θ \theta θ角度,可以通过基本滤波器的相位来控制合成滤波器:
ρ θ Ψ ( x ) = ∑ j = 1 J ∑ k = 0 K w j k e − i k θ ψ j k ( x ) , 等 式 5 {\rho _\theta }\Psi (x) = \sum\limits_{j = 1}^J {\sum\limits_{k = 0}^K {{w_{jk}}} } {e^{ - {\rm{i}}k\theta }}{\psi _{jk}}(x){,等式5} ρθΨ(x)=j=1∑Jk=0∑Kwjke−ikθψjk(x),等式5滤波器的单个方向可以通过取复数的实数部分表示,表示为 R e Ψ ( x ) {\mathop{\rm Re}\nolimits} \Psi (x) ReΨ(x)。
(3)CNN旋转等变性
Learning Steerable Filters for Rotation Equivariant CNNs
实现CNN对平移和任意离散旋转的等变性。使用多个复数滤波器,通过权重相加,得到最后的滤波器。其中,单个原子滤波器是已知的,权重需要学习。卷积时用的是复数滤波器的实数部分。
(4)RE-SiamNet
RE-SiamNet在SiamFC基础上进行修改。
SiamFC基本结构:输入层、卷积层、互相关。
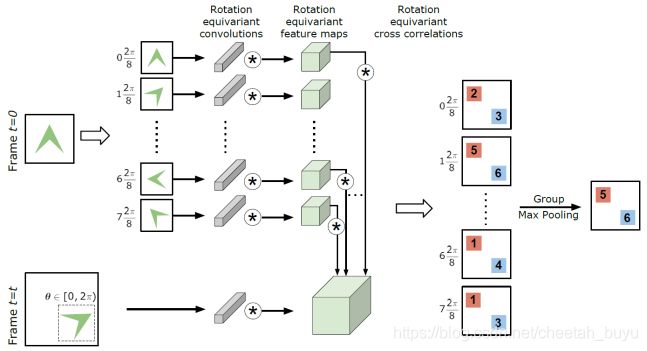
RE-SiamNet则用旋转等边模块替换这些层。引入组最大池化模块(Group Max Pooling),为生成的多个响应图选择最合适的方向进行互相关。
Siamese跟踪器生成响应图 h ( z , x ) h(z,x) h(z,x):
h ( z , x ) = f ( z ) ∗ f ( x ) , 等 式 6 h(z,x) = f(z)*f(x){,等式6} h(z,x)=f(z)∗f(x),等式6其中,z和x分别表示模板图帧候选帧, f ( ⋅ ) f(\cdot) f(⋅)是特征提取, ∗ * ∗表示卷积运算。
Rotation equivariant input(旋转等变输入)
搜索分支:单个搜索图像作为输入
模板分支:模板图像、模板帧的多个旋转体的集合Z,其中 Z = { z 1 , z 2 , … , z Λ } Z = \left\{ {{z_1},{z_2}, \ldots ,{z_\Lambda }} \right\} Z={z1,z2,…,zΛ}
每个输入图像I包括C个通道,每个通道上的图像函数被表示为 I c {I_c} Ic,并且 c ∈ { 1 , 2 , … , C } c\in \{ 1,2, \ldots ,C\} c∈{1,2,…,C} 。通道上 θ \theta θ 旋转的卷积核 ρ θ Ψ c ^ c {\rho _\theta }{\Psi _{\hat cc}} ρθΨc^c,然后将此输入与通道 c ^ \hat c c^上的旋转卷积核 ρ θ Ψ c ^ c {\rho _\theta }{\Psi _{\hat cc}} ρθΨc^c进行卷积,其中, c ^ ∈ { 1 , 2 , … , C ^ } \hat c \in \{ 1,2, \ldots ,\hat C\} c^∈{1,2,…,C^}。 基于等式5,通道 c ^ \hat c c^未经过非线性处理的最终特征:
y c ~ 1 ( x , θ ) = R e ∑ c = 1 C ∑ j = 1 J ∑ k = 0 K j w c ^ c j k e − i k θ ( I c ∗ ψ j k ) ( x ) , 等 式 7 y_{_{{\rm{\tilde c}}}}^1(x,\theta ) = {\mathop{\rm Re}\nolimits} \sum\limits_{c = 1}^C {\sum\limits_{j = 1}^J {\sum\limits_{k = 0}^{{K_j}} {{w_{\hat ccjk}}} } } {e^{ - ik\theta }}\left( {{I_c}*{\psi _{jk}}} \right)(x) {,等式7} yc~1(x,θ)=Rec=1∑Cj=1∑Jk=0∑Kjwc^cjke−ikθ(Ic∗ψjk)(x),等式7然后将滤波器按照等距方向 θ \theta θ旋转变形,该等距方向由集合 Θ = { 0 , Λ , … , 2 π Λ − 1 Λ } \Theta = \left\{ {0,\Lambda , \ldots ,2\pi \frac{{\Lambda - 1}}{\Lambda }} \right\} Θ={0,Λ,…,2πΛΛ−1}表示。然后应用偏置项 β c ^ {\beta _{\hat c}} βc^和非线性σ来获得第一层 ζ c ^ {\zeta _{\hat c}} ζc^处的特征图。
Rotation equivariant convolutions(旋转等变卷积)
由等式7产生的特征图使用group卷积进一步处理,从而在更广泛的一组转换组上推广空间卷积。 与第一层相似,可控滤波器在group上定义为:
y c ^ ( l ) ( x , θ ) = R e ∑ c = 1 C ∑ ϕ ∈ Θ ∑ j , k w c ^ c j k , θ − ϕ e − i k θ ( ζ c ( l − 1 ) ( ⋅ , ϕ ) ∗ ψ j k ) ( x ) , 等 式 8 y_{\hat c}^{(l)}(x,\theta ) = {\mathop{\rm Re}\nolimits} \sum\limits_{c = 1}^C {\sum\limits_{\phi \in \Theta } {\sum\limits_{j,k} {{w_{\hat ccjk,\theta - \phi }}} } } {e^{ - {\rm{i}}k\theta }}(\left. {\zeta _c^{(l - 1)}( \cdot ,\phi )*{\psi _{jk}}} \right)(x) {,等式8} yc^(l)(x,θ)=Rec=1∑Cϕ∈Θ∑j,k∑wc^cjk,θ−ϕe−ikθ(ζc(l−1)(⋅,ϕ)∗ψjk)(x),等式8在等式8中引入了权量张量的附加指标 θ − ϕ \theta - \phi θ−ϕ,便于沿着旋转维度进行群卷积运算。它涉及到通过空间旋转来改变组上的功能。
Rotation equivariant pooling(旋转等变池化)
最后一组卷积层的输出通过在旋转维度上的池化进行进一步处理。与传统的分类任务不同,池化不是沿着空间维度来保持旋转等变性。
Rotation equivariant cross-correlation(旋转等变互相关)
从RE-SiamNet模块的两个子网中,我们获得了两组特征图, { ϕ ( z ) } \{ \phi (z)\} {ϕ(z)}和 ϕ ( x ) \phi (x) ϕ(x),其中, { ϕ ( z ) } \{ \phi (z)\} {ϕ(z)}是包含 Λ \Lambda Λ方向上的特征图的集合。 接下来,对 { ϕ ( z ) } \{ \phi (z)\} {ϕ(z)}和 ϕ ( x ) \phi (x) ϕ(x)进行卷积以获得 { h ^ ( z , x ) } \{ \hat h(z,x)\} {h^(z,x)},这是一组 Λ \Lambda Λ响应图,其中 h i ( z , x ) = ϕ ( z i ) ∗ ϕ ( x ) {h_i}(z,x) = \phi \left( {{z_i}} \right)*\phi (x) hi(z,x)=ϕ(zi)∗ϕ(x)。 接下来,使用全局最大池化操作对 { h ^ ( z , x ) } \{ \hat h(z,x)\} {h^(z,x)}进行处理,以获得最终的输出响应图 h ( Z , x ) h(Z,x) h(Z,x)。 全局池化中的最大值,并选择包含该最大值的特征图。
(5)构建RE-SiamNet 框架
- 通过区分旋转自由度的不同方向来确定跟踪器的精度。基于 Λ \Lambda Λ旋转组,RE-SiamNet将与由 Θ = { ( i − 1 ) ⋅ 360 / Λ } i = 1 Λ \Theta = \{ (i - 1) \cdot 360/\Lambda \} _{i = 1}^\Lambda Θ={(i−1)⋅360/Λ}i=1Λ定义的角度完全相等。
- 根据现有的Siam跟踪器定义非参数编码 ϕ ( . ) \phi (.) ϕ(.)。 根据 ϕ ( . ) \phi (.) ϕ(.)的选择,跟踪器的判别力会有所不同。
- 用等变旋转模块替换所有卷积层 ϕ ( . ) \phi (.) ϕ(.)。
- 代替单个卷积生成 h ( z , x ) h(z,x) h(z,x),执行 Λ \Lambda Λ卷积以生成 Λ \Lambda Λ不同的响应图。
- 对特征图执行全局最大池化以生成 h ( Z , x ) h(Z,x) h(Z,x),然后对其进行处理以定位目标。
请注意,根据跟踪器头部的选择,对 h ( Z , x ) h(Z,x) h(Z,x)的处理操作可能会有所不同。例如,对于诸如SINT和SiamFC之类的跟踪器,前一帧的姿态目标将以不同的比例和宽高比进行拟合,并从中选择最佳。对于诸如SiamRPN和SiamRPN++之类的其他跟踪器,添加了区域建议模块RPN,该模块使用神经网络头部对边框进行回归。在我们的跟踪体系结构中,旋转等变只需要保持到 h ( Z , x ) h(Z,x) h(Z,x),因此可以使用这些方法中的任何一种。
(6)Unsupervised Relative Rotation Estimation(无监督相对旋转估计)
Unsupervised 2D pose estimation(无监督2D姿态估计)
RE-SiamNet可以在完全无人监督的情况下获得目标2D姿态相对变化的估计值。该信息可以从组最大池化步骤的结果中获得。
设 i ∈ { 1 , 2 , … , Γ } i \in \{ 1,2, \ldots ,\Gamma \} i∈{1,2,…,Γ},表示模板图像的方向 Λ \Lambda Λ。
h ( Z , x ) = h ^ ( z i , x ) = g r o u p − m a x p o o l ( { h ( z , x ) } ) , 等 式 9 h(Z,x) = \hat h\left( {{z_i},x} \right) = {\mathop{\rm group}\nolimits} - {\mathop{\rm maxpool}\nolimits} (\{ h(z,x)\} ) {,等式9} h(Z,x)=h^(zi,x)=group−maxpool({h(z,x)}),等式9其中,i是模板图像姿态与其在候选图像中出现的姿态不同的旋转组数。
以旋转角度 θ d i f f {\theta _{diff}} θdiff表示的姿态差为 i ⋅ 360 / Γ i \cdot 360/\Gamma i⋅360/Γ 。建设目标的实际平面内旋转为 θ c {\theta _c} θc,则预测误差度数为 ∣ θ d i f f − θ c ∣ ≤ 360 2 Λ \left| {{\theta _{{\rm{diff }}}} - {\theta _c}} \right| \le \frac{{360}}{{2\Lambda }} ∣θdiff−θc∣≤2Λ360。所以,对于较大的旋转角度 Λ \Lambda Λ,姿态估计的误差较小。

Rotational Motion Consistency(旋转运动一致性)
这个运动约束可改善目标跟踪中的时间对应性。在选择 Λ \Lambda Λ方向 θ o p t ∈ Θ {\theta _{{\rm{opt }}}} \in \Theta θopt∈Θ的过程中实现。设 θ t , o p t = θ t , i {\theta _{t,{\rm{opt}}}} = {\theta _{t,i}} θt,opt=θt,i ,其中, θ t , i {\theta _{t,i}} θt,i表示t帧中的第i个方向。选择下一帧时,不从整个集合 θ \theta θ中选择 θ t + 1 , o p t {\theta _{t + 1,opt}} θt+1,opt,而是施加约束,使 θ t + 1 , o p t ∈ { θ i } {\theta _{t + 1,opt}} \in \left\{ {{\theta _i}} \right\} θt+1,opt∈{θi},其中, i ∈ { i t , o p t − γ , … , i t , o p t − 1 , i t , o p t , i t , o p t + 1 , … , i t , o p t + γ } i \in \left\{ {{i_{t,{\rm{opt}}}} - \gamma , \ldots ,{i_{t,{\rm{opt}}}} - 1,{i_{t,{\rm{ opt }}}},{i_{t,{\rm{opt}}}} + } \right.\left. {1, \ldots ,{i_{t,{\rm{ opt }}}} + \gamma } \right\} i∈{it,opt−γ,…,it,opt−1,it,opt,it,opt+1,…,it,opt+γ}, γ \gamma γ是两个连续帧之间任意方向上允许的方向数的最大变化。这一约束保证了在两个连续帧之间的取向变化不超过 γ \gamma γ组。
(7)Rotating Objects Benchmark(ROB)
最先进的基准测试大多不包含旋转注释。为了评估RE-SiamNets,并在rotation sensitive tracking(旋转敏感跟踪)、unsupervised rotation estimation(无监督旋转估计)和rotation stabilization(旋转稳定)方面实现未来的基准,本文提出ROB(旋转对象基准),由目标对象在平面内大尺度旋转的真实视频序列组成。
Rot-MNIST
图片背景从GOT10K训练集中提取,再加上MNIST数字。每个视频由浮动的MNIST数字和旋转的目标数字组成。平移和旋转运动都由布朗方程控制。训练集包含2500个序列,只显示平移运动,而测试集包含100个序列,包括平移和旋转。训练集和测试集的每个序列都包含100帧。从测试集的3个序列中随机抽样的帧如图5所示。
Rot-OTB00
Rot-OTB100是通过旋转原始OTB100数据集的图像帧构建的数据集。为此,每个序列都是从第一帧开始,每一帧相对于前一帧逆时针旋转0.5度。为了保持数据集结构类似于OTB,我们没有使用旋转的边框,而是使用常规的边框。选择边界框的方式是,使原始边界框的旋转版本(在旋转后获得)紧紧地适合于它。因此,Rot-OTB100是一个与OTB100序列数量完全相同的测试集,除了帧被旋转。
ROB
ROB数据集包括35个视频序列,每个视频序列300~500帧,超过10,000个带注释的帧和15个对象类别,包括广泛的现实场景,如牲畜监测,自行车和飞机。其中目标对象由于摄像机的旋转或对象本身的平面旋转而经历旋转。每帧提供ground truth和方向信息。为了标注方向变化,在第一帧中沿着目标的一个轴绘制一个单箭头,并在其余帧中始终跟随。这允许在任意两帧中计算目标外观之间的方向变化。
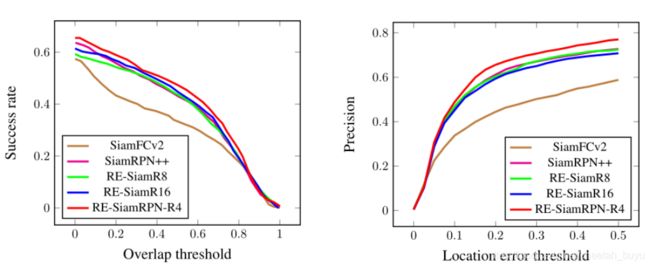
4.Experiments
为了设计RE-SiamNets,我们对现有模型进行了调整,将常规CNN层替换为旋转等变层,并使用组池化对每个输入进行单方向输出特征。这些旋转等变模块是使用e2cnn pytorch库添加的。对于基本的Siamese跟踪器,我们使用SiamFC、它的变体SiamFCv2和SiamRPN++。在这里和以后,我们使用前缀“RE-”来表示跟踪器的旋转等变版本。