数据挖掘——航空公司客户价值分析（分析+建模）

前言

本次建模项目是来自于《python数据分析与挖掘实战》的案例，是介绍航空公司客户价值的分析，书中给出了关于62988个客户的基本信息和在观测窗口内的消费积分等相关信息，其中包含了会员卡号、入会时间、性别、年龄、会员卡级别、在观测窗口内的飞行公里数、飞行时间等44个特征属性，并用到的聚类方法是K-Means方法。

本文是为2019年数学建模做准备，在原文基础上，进行了部分改进，主要步骤如下：

1. 数据探索性分析——数据的分布情况
2. 数据预处理——缺失值和异常值分析与清理
3. 属性规约——构造有价值的属性
4. 数据变换——标准化
5. 构造模型——K-means
6. 引入SSE评价K值
7. 绘制可视化图表

1. 数据探索性分析

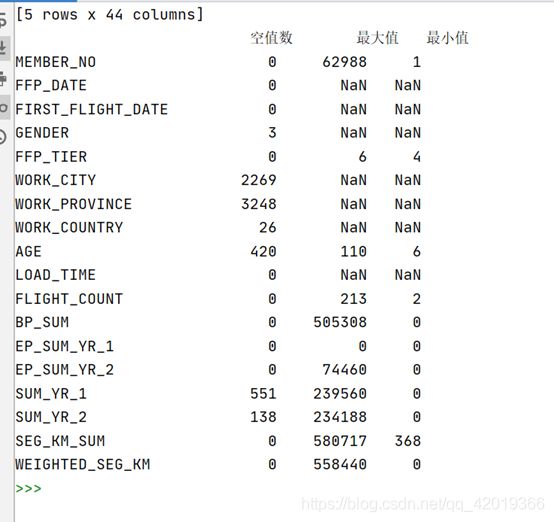
将数据读取到程序中，并查看每个特征属性的相关信息，以便对“脏”数据进行处理：

datafile = "air_data.csv"
data = pd.read_csv(datafile,
encoding="utf-8")
print(data.shape)
print(data.info())

截取部分输出图如下

#包括对数据的基本描述，percentiles参数是指定计算多少的分为数表(如1/4分位数、中位数等)
#describe() 函数可以查看数据的基本情况，
explore = data.describe(percentiles = [], include = 'all').T #转置后方便查阅
#describe()函数自动计算非空值数，需要手动计算空值数
explore['null'] = len(data) - explore['count']
explore = explore[['null', 'max', 'min']]
explore.columns = [u'空值数', u'最大值', u'最小值']  #表头重命名
print(explore)

plt.rcParams['font.sans-serif'] = ['SimHei']  #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  #用来正常显示负号#探索客户的基本信息分布情况
#客户信息类别
#提取会员入会年份
ffp = data['FFP_DATE'].apply(lambda x:datetime.strptime(x, '%Y/%m/%d'))
ffp_year = ffp.map(lambda x : x.year)
print(ffp_year)
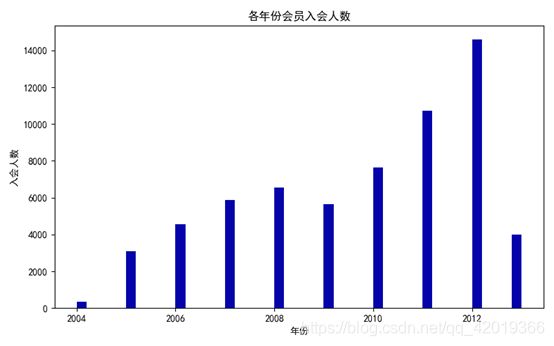
#绘制各年份会员入会人数直方图
fig = plt.figure(figsize=(8, 5))  #设置画布大小
plt.hist(ffp_year, bins='auto', color='#0504aa')
plt.xlabel('年份')
plt.ylabel('入会人数')
plt.title('各年份会员入会人数')
plt.show()
plt.close()

#提取会员不同性别人数
male = pd.value_counts(data['GENDER'])['男']
female = pd.value_counts(data['GENDER'])['女']
#绘制会员性别比例饼图
fig = plt.figure(figsize=(7, 4))  #设置画布大小
plt.pie([male, female], labels=['男', '女'], colors=['lightskyblue', 'lightcoral'], autopct='%1.1f%%')
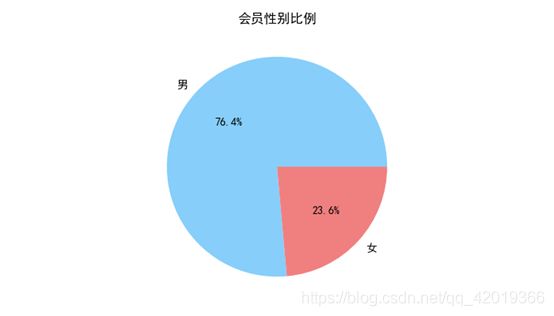
plt.title('会员性别比例')
plt.show()
plt.close()

#提取不同级别会员的人数
lv_four = pd.value_counts(data['FFP_TIER'])[4]
lv_five = pd.value_counts(data['FFP_TIER'])[5]
lv_six = pd.value_counts(data['FFP_TIER'])[6]
#绘制会员各级别人数条形图
fig = plt.figure(figsize=(8,5))  #设置画布大小
plt.bar(range(3), [lv_four, lv_five, lv_six], width=0.4, alpha=0.8, color='skyblue')
#left：x轴的位置序列，一般采用arange函数产生一个序列；
#height：y轴的数值序列，也就是柱形图的高度，一般就是我们需要展示的数据；
#alpha：透明度
#width：为柱形图的宽度，一般这是为0.8即可；
#color或facecolor：柱形图填充的颜色；
plt.xticks([index for index in range(3)], ['4', '5', '6'])
plt.xlabel('会员等级')
plt.ylabel('会员人数')
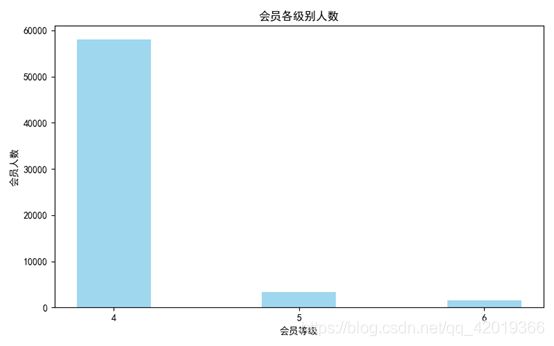
plt.title('会员各级别人数')
plt.show()
plt.close()

#提取会员年龄
age = data['AGE'].dropna()
age = age.astype('int64')
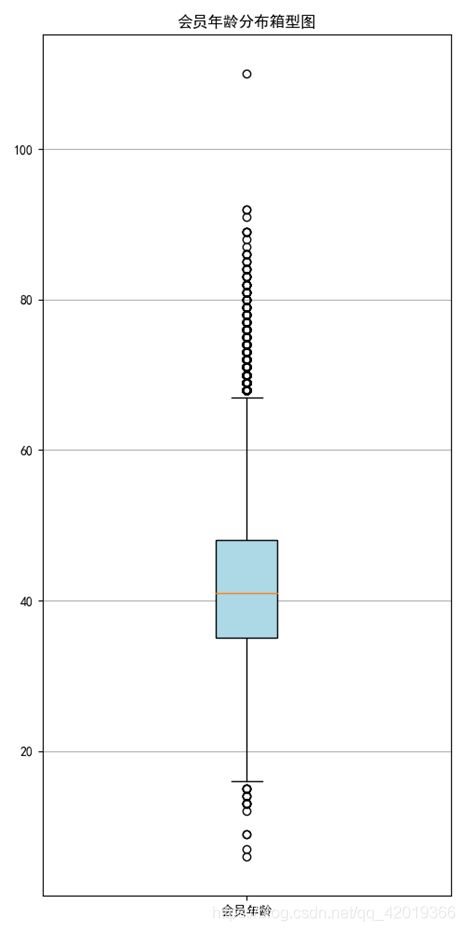
#绘制会员年龄分布箱型图
fig = plt.figure(figsize=(5,10))
plt.boxplot(age, patch_artist=True, labels=['会员年龄'], boxprops={'facecolor': 'lightblue'}) #设置填充颜色
plt.title('会员年龄分布箱型图')
#显示y坐标轴的底线
plt.grid(axis='y')
plt.show()
plt.close()

#3相关性分析
#提取属性并合并为新的数据集
data_corr = data.loc[:,['FFP_TIER', 'FLIGHT_COUNT', 'LAST_TO_END', 'SEG_KM_SUM', 'EXCHANGE_COUNT', 'Points_Sum']]
age1 = data['AGE'].fillna(0)
data_corr['AGE'] = age1.astype('int64')
data_corr['ffp_year'] = ffp_year

#计算相关性矩阵
dt_corr = data_corr.corr(method='pearson')
print('相关性矩阵为：\n', dt_corr)

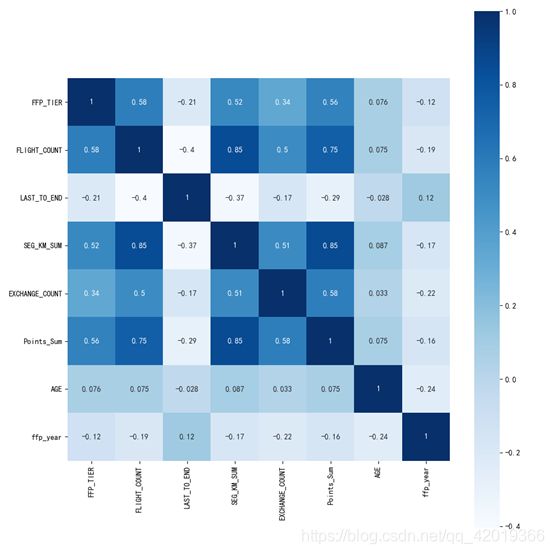
#绘制热力图
plt.subplots(figsize=(10, 10))  #设置画面大小
## data:数据 square:是否是正方形 vmax:最大值 vmin:最小值 robust:排除极端值影响
sns.heatmap(dt_corr, annot=True, vmax=1, square=True, cmap='Blues')
plt.show()
plt.close()

通过探索性分析可以发现：用户入会人数最多的年份是2012年左右，性别以男性为主占比达76.4%，会员等级以VIP4为主，年龄主要分布于40岁上下。因此，对于航空行业的客户而言，其画像主要以40岁且较频繁出差的男性为主。同时根据相关性分析可知： “Points_Sum", “FLIGHT_COUNT”, “SEG_KM_SUM”,“EXCHANGE_COUNT”互为强相关属性。
因此我们可以初步认定，航空公司会员客户以工作出差为主，因此以出差的频率和周期为切入点，是一个很好的选择。

2. 数据预处理

在探索性分析之后，我们对数据具有一个初步判断。在此基础之上，我们进行数据清洗工作。
通过观测可知，数据集中存在异常数据：票价为0，但飞行公里大于0。所占比例较小，这里直接删去处理。

data = data[data["SUM_YR_1"].notnull() & data["SUM_YR_2"].notnull()]
index1 = data["SUM_YR_1"] != 0
index2 = data["SUM_YR_2"] != 0
index3 = (data["SEG_KM_SUM"] == 0) & (data["avg_discount"] == 0)
data = data[index1 | index2| index3]
print(data.shape)

删除后剩余的样本值是62044个，可见异常样本的比例不足1.5%。

3. 属性规约——构造有价值的属性

原始数据集的特征属性太多，而且各属性不具有降维的特征，这里并没有完全按照书中的做法选取特征，而是根据前文探索性分析所发现的切入点：出差频率与周期。因此主要分为三个层面：公司盈利、客户价值和客户需求。

因此，本实验最终选取的特征是第一年总票价、第二年总票价、观测窗口总飞行公里数、飞行次数、平均乘机时间间隔、观察窗口内最大乘机间隔、入会时间、观测窗口的结束时间、平均折扣率共8个特征。

1. 第一年总票价、第二年总票价、观测窗口总飞行公里数是要计算平均飞行每公里的票价，因为对于航空公司来说并不是票价越高，行公里数越长越能创造利润，相反而是那些近距离的高等舱的客户创造更大的利益。

2. 总飞行公里数、飞行次数也都是评价一个客户价值的重要的指标。

3. 入会时间可以看出客户是不是老用户及忠诚度。

4. 通过平均乘机时间间隔、观察窗口内最大乘机间隔可以判断客户的乘机频率和周期是否具有一定规律性。

5. 平均折扣率可以反映出客户给公司带来的利益，毕竟来说越是高价值的客户享用的折扣率越高

选择属性

filter_data = data[[ "FFP_DATE", "LOAD_TIME", "FLIGHT_COUNT", "SUM_YR_1", "SUM_YR_2", "SEG_KM_SUM", "AVG_INTERVAL" , "MAX_INTERVAL", "avg_discount"]]
filter_data[0:5]

构建特征

data["LOAD_TIME"] = pd.to_datetime(data["LOAD_TIME"])
data["FFP_DATE"] = pd.to_datetime(data["FFP_DATE"])
data["入会时间"] = data["LOAD_TIME"] - data["FFP_DATE"]
data["平均每公里票价"] = (data["SUM_YR_1"] + data["SUM_YR_2"]) / data["SEG_KM_SUM"]
data["时间间隔差值"] = data["MAX_INTERVAL"] - data["AVG_INTERVAL"]
deal_data = data.rename(
    columns = {"FLIGHT_COUNT" : "飞行次数", "SEG_KM_SUM" : "总里程", "avg_discount" : "平均折扣率"},
    inplace = False
)

filter_data = deal_data[["入会时间", "飞行次数", "平均每公里票价", "总里程", "时间间隔差值", "平均折扣率"]]
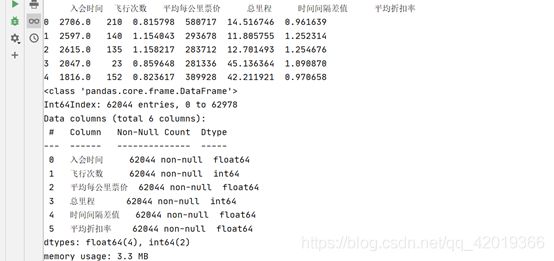
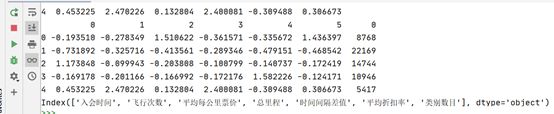
print(filter_data[0:5])
filter_data['入会时间'] = filter_data['入会时间'].astype(np.int64)/(60*60*24*10**9)
print(filter_data[0:5])
print(filter_data.info())

4. 数据变换——标准化

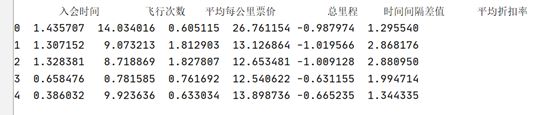
由于不同的属性相差范围较大，这里进行标准化处理。

filter_zscore_data = (filter_data -filter_data.mean(axis=0))/(filter_data.std(axis=0))
filter_zscore_data[0:5]

5. 构建模型

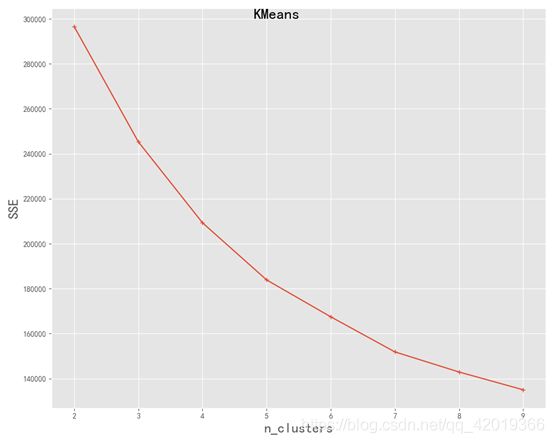
对于K-Means方法，k的取值是一个难点。本实验采用计算SSE的方法，尝试找到最好的K数值。编写函数如下：

def distEclud(vecA, vecB):
    """
    计算两个向量的欧式距离的平方，并返回
    """
    return np.sum(np.power(vecA- vecB, 2))

def test_Kmeans_nclusters(data_train):
    """
    计算不同的k值时，SSE的大小变化
    """
    data_train = data_train.values
    nums = range(2, 10)
    SSE = []
    for num in nums:
        sse = 0
        kmodel = KMeans(n_clusters=num, n_jobs=4)
        kmodel.fit(data_train)
        # 簇中心
        cluster_ceter_list = kmodel.cluster_centers_
        # 个样本属于的簇序号列表
        cluster_list= kmodel.labels_.tolist()
        for index in range(len(data)):
            cluster_num = cluster_list[index]
            sse += distEclud(data_train[index, :], cluster_ceter_list[cluster_num])
        print("簇数是",num, "时； SSE是",sse)
        SSE.append(sse)
    return nums,SSE
nums, SSE = test_Kmeans_nclusters(filter_zscore_data)
#输出结果
簇数是 2 时； SSE是 296588.1808562679
簇数是 3 时； SSE是 245318.74245294172
簇数是 4 时； SSE是 209301.99322383406
簇数是 5 时； SSE是 183887.43155015737
簇数是 6 时； SSE是 167466.5070077715
簇数是 7 时； SSE是 151869.94302542473

绘制SSE图

#画图，通过观察SSE与k的取值尝试找出合适的k值
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['font.size'] = 12.0
plt.rcParams['axes.unicode_minus'] = False

# 使用ggplot的绘图风格
plt.style.use('ggplot')

## 绘图观测SSE与簇个数的关系
fig=plt.figure(figsize=(10, 8))
ax=fig.add_subplot(1,1,1)
ax.plot(nums,SSE,marker="+")
ax.set_xlabel("n_clusters", fontsize=18)
ax.set_ylabel("SSE", fontsize=18)
fig.suptitle("KMeans", fontsize=20)
plt.show()

观察图像，并没有的所谓的“折”点出现，是随k值的增大逐渐减小的，这里选取当k分别取4， 5， 6时进行，最后通过筛选选择k=5：

绘制可视化图表

kmodel = KMeans(n_clusters=4, n_jobs=4)
kmodel.fit(filter_zscore_data)

# 简单打印结果
r1 = pd.Series(kmodel.labels_).value_counts()  # 统计各个类别的数目
r2 = pd.DataFrame(kmodel.cluster_centers_)  # 找出聚类中心

# 所有簇中心坐标值中最大值和最小值
max = r2.values.max()
min = r2.values.min()
r = pd.concat([r2, r1], axis=1)  # 横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(filter_zscore_data.columns) + [u'类别数目']  # 重命名表头

# 绘图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, polar=True)
center_num = r.values
feature = ["入会时间", "飞行次数", "平均每公里票价", "总里程", "时间间隔差值", "平均折扣率"]
N = len(feature)

for i, v in enumerate(center_num):
    # 设置雷达图的角度，用于平分切开一个圆面
    angles = np.linspace(0, 2 * np.pi, N, endpoint=False)
    # 为了使雷达图一圈封闭起来，需要下面的步骤
    center = np.concatenate((v[:-1], [v[0]]))
    angles = np.concatenate((angles, [angles[0]]))
    # 绘制折线图
    ax.plot(angles, center, 'o-', linewidth=2, label="第%d簇人群,%d人" % (i + 1, v[-1]))
    # 填充颜色
    ax.fill(angles, center, alpha=0.25)
    # 添加每个特征的标签
    ax.set_thetagrids(angles * 180 / np.pi, feature, fontsize=15)
    # 设置雷达图的范围
    ax.set_ylim(min - 0.1, max + 0.1)
    # 添加标题
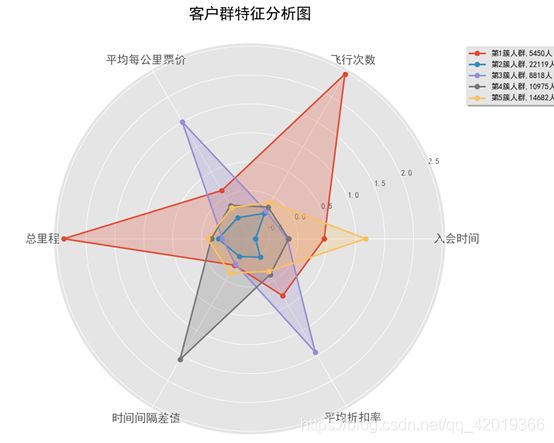
    plt.title('客户群特征分析图', fontsize=20)
    # 添加网格线
    ax.grid(True)
    # 设置图例
    plt.legend(loc='upper right', bbox_to_anchor=(1.3, 1.0), ncol=1, fancybox=True, shadow=True)
# 显示图形
plt.show()

1. 第一簇人群，5443人，总里程和飞行次数都是最多的，而且平均每公里票价也较高，属于重点维护对象；
2. 第二簇人群，22119人，各方面的数据都是比较低的，属于一般或低价值用户；
3. 第三簇人群，8818人，；最大的特点就是平均每公里票价和平均折扣率都是最高的，属于乘坐高等舱的商务人员，应该重点维护，也需要重点发展，另外应该积极采取相关的优惠政策是他们的乘坐次数增加；
4. 第四簇人群，10957人，最大的特点是时间间隔差值最大，分析可能是“季节周期型客户”，一年中在某个时间段需要多次乘坐飞机进行旅行，其他的时间则出行的不多，这类客户我们需要在维护的前提下，进行一定的发展；
5. 第五簇人群，14682人，最大的特点就是入会的时间较长，属于老客户按理说平均折扣率应该较高才对，但是观察窗口的平均折扣率较低，且总里程和总次数都不高，分析属于即将流失的客户，需要进行回访并争取维护。