房价预测:EDA+ElasticNet+Xgboost
房屋的价格取决于很多因素,就拿美国的房屋来说(咱中国情况特殊)房屋的价格取决于所在的区域,房屋的面积,卧室的数量,卫生间的数量,院子的大小,地下室的面积,车库的数量等等很多变量。在众多的变量中房屋所在区域应该对房屋价格影响最大,但是相同区域的房价,也会因为其他变量的不同而有所差异。今天我们就拿kaggle中的一个案例来分析一下房屋价格和其他变量之间存在的关系,并通过可视化的方式来呈现出这种关系,接着我们要使用ElasticNet和xgboost来创建几个回归模型对价格进行预测,最后我们要评估这些模型的性能,并从中找出表现最好的模型。通过对这个案例数据的分析,可以让大家掌握一些基本的统计学的基础知识如正太分布,均值、标准差、理论分位图(QQ图)、相关系数等知识,这对应想从事数据分析工作的朋友来说有很大的帮助。
EDA(探索性数据分析)
你可以从这里下载我们的数据,然后加载我们所需要的一些包
%matplotlib inline
import numpy as np
import pandas as pd
from scipy import stats
from scipy.stats import norm, skew
from sklearn import preprocessing
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import ElasticNetCV, ElasticNet
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import StratifiedKFold
from xgboost import XGBRegressor, plot_importance
import matplotlib.pyplot as plt
import seaborn as sns
def ignore_warn(*args, **kwargs):
pass
import warnings
warnings.warn = ignore_warn
pd.set_option('display.float_format', lambda x: '{:.3f}'.format(x))如果有发现某些包没有安装,那请在jupyter notebook中使用 !pip install xxx 进行安装。加载完所需要的包以后,我们导入我们的数据:
df = pd.read_csv('./data/house/train.csv')
print(df.shape)
df.head()总共有1460条记录,共有81列,其中SalePrice是我们的目标变量,除去SalePrice和Id这两列以外,其余79个变量都是我们的特征变量,这些特征变量的含义在这我就不一一说明了(因为实在太多),大家可以查看kaggle中的Data Description。接下来我们要做数据清洗的工作,因为有很多字段有空值,我们必须要清洗掉这些数据,首先我们要查询一下数据中的空值情况:
(df.isnull().sum() / len(df)).sort_values(ascending=False)[:20]我们查看了前20个包含空值最多的变量(字段),其中PoolQC、MiscFeature、Alley、Fence这4个变量所包含空值的比例都在90%和80%以上,它们包含了大量的空值。所以我们要删除这些变量,同时为了便于后续的分析,我们还要同时删除Id字段。
df.drop(['PoolQC', 'MiscFeature', 'Alley', 'Fence', 'Id'], axis=1, inplace=True)目标变量
SalePrice是我们的目标变量,也是最后我们要预测的变量,所以我们要对它进行深入分析,首先我们要查看SalePrice的数据分布情况。
sns.distplot(df['SalePrice'] , fit=norm);
#得到均值和标准差
(mu, sigma) = norm.fit(df['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
plt.ylabel('Frequency')
plt.title('Sale Price distribution')
#画QQ图
fig = plt.figure()
res = stats.probplot(df['SalePrice'], plot=plt)
plt.show();上面那个图是SalePrice的数据分布图(直方图),同时我们用正太分布对它进行拟合,并得到了两个参数均值(μ)和标准差(σ),用肉眼就能看出SalePrice出现右偏(右侧有长尾),严重偏离正态分布。底下的是QQ图(理论分位数图),它的主要作用是判断样本是否近似于某种类型的分布,如果图中的蓝色点偏离了红线,说明数据不服从正太分布(如果蓝点紧紧围绕红线,那就是服从正态分布)。
纠偏
当发现SalePrice呈现偏斜的分布以后,我们要对它进行纠偏,我们要数据进行对数化处理,这类似与机器学习中的归一化处理的概念,是一种数据标准化处理的方法。
sns.distplot(np.log1p(df['SalePrice']) , fit=norm);
# 纠偏,对数化处理。
(mu, sigma) = norm.fit(np.log1p(df['SalePrice']))
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
#纠偏后再化分布图
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
plt.ylabel('Frequency')
plt.title('log(Sale Price+1) distribution')
#画QQ图
fig = plt.figure()
res = stats.probplot(np.log1p(df['SalePrice']), plot=plt)
plt.show();经过纠偏处理以后SalePrice基本服从正太分布。
特征变量之间的相关性研究
接下来我们要研究的是除SalePrice以外的所有特征变量之间的相关性,我们要画一个所有特征变量(数字型的)之间的相关系数矩阵的热力图:
pd.set_option('precision',2)
plt.figure(figsize=(10, 8))
sns.heatmap(df.drop(['SalePrice'],axis=1).corr(), square=True)
plt.suptitle("Pearson Correlation Heatmap")
plt.show();皮尔森相关系数用来表示两个变量之间存在关联关系的强弱程度(即一个变量发生变化则另外一个变量也随之发生变化),相关系数的取值范围是[-1,1],其中-1表示完全负相关,1表示完全正相关,0表示不相关,在上面的相关系数矩阵中的热图中,色块的颜色越浅(如主对角线呈现白色)表示越呈现正相关越强,颜色越深表示越呈现负相关越强。如上图中YearBuilt和OverallCond这两个变量对应的色块是黑色的,说明有非常强的负相关,YearBuilt表示房屋的建造年份,OverallCond表示总体评级,也是就是房龄越长,总体评级越低。
目标变量和特征变量之间的相关性研究
我们完成了特征变量之间的相关性研究以后,接下来我们要进行目标变量SalePrice与我们的特征变量之间的相关性研究。
corr_with_sale_price = df.corr()["SalePrice"].sort_values(ascending=False)
plt.figure(figsize=(14,6))
corr_with_sale_price.drop("SalePrice").plot.bar()
plt.show();我们看到大部分变量与目标变量呈现正相关,有少部分变量呈现负相关。其中OverallQual与目标变量的相关性最大接近80%,我查询了一下OverallQual表示"整体材料和成品质量",这符合常理,房屋的材料和质量越好,房屋的价格应该越高。KitchenAbvGr与目标变量呈现最强的负相关,经过查询KitchenAbvGr表示地面厨房数量,也就是说地面厨房数量越多,房屋价格越低,这是否意味着地面厨房数量越多,房屋的有效使用面积就越小,所以房价就越低?咱没有住过美国的那种独栋别墅,所以只能瞎猜了。下面我们查看一下与目标变量相关性最强的特征变量OverallQual的箱体图
var = 'OverallQual'
data = pd.concat([df['SalePrice'], df[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000)可以看到随着OverallQual:"整体材料和成品质量"的数值的提高,价格的中位数明显上升,显示出很强的正相关性。
接下来我们查看几个变量的散点图:
#多变量散点图
sns.pairplot(df[['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars']])
plt.show();你可以找出哪几个变量之间是正相关的吗?它们的相关性与之前的相关系数矩阵热图是否一致?
数据清洗
上面我们完成了对数据的分析工作,接下来我们要开始清洗数据,以便为后续的模型训练做好准备工作,数据清洗需要完成以下一些工作:
- 对目标变量和特征变量进行纠偏(对数化处理)
- 对分类型变量进行one-hot编码
- 用特征变量的均值来填充空值
- 创建训练集和测试集
print("数据清洗前的特征变量的数量为:",len(df.columns)-1)
#对目标变量进行对数化纠偏
df["SalePrice"] = np.log1p(df["SalePrice"])
#对数值型特征变量进行对数化处理:1.过滤出数值型变量,2.计算偏度,3.对偏度大于0.75的数据进行对数化纠偏
#1.过滤出数值型变量
numeric_feats = df.dtypes[df.dtypes != "object"].index
#2.计算偏度
skewed_feats = df[numeric_feats].apply(lambda x: skew(x.dropna())) #compute skewness
skewed_feats = skewed_feats[skewed_feats > 0.75]
skewed_feats = skewed_feats.index
#3.对偏度大于0.75的数据进行对数化纠偏
df[skewed_feats] = np.log1p(df[skewed_feats])
#4.对分类型变量进行one-hot编码,分类型变量会被横向展开为多个变量
df = pd.get_dummies(df)
#用均值填充空值
df = df.fillna(df.mean())
print("数据清洗后的特征变量的数量为:",len(df.columns)-1)
#创建训练集和测试集
X, y = df.drop(['SalePrice'], axis = 1), df['SalePrice']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)特征变量的数量,由原来的75个,变成了现在的275个,这是因为我们对分类型变量做了one-hot编码(pd.get_dummies),经过这样处理以后,原来的分类型变量会被横向展开为多个变量,因此特征变量的总数会增加很多。偏度skew是指偏离正太分布的程度,对于正态分布数据,偏度应约为0.,偏度值> 0意味着数据分布呈现右偏,偏度值<0意味着数据分布呈现左偏。 在统计学上,函数skewtest可用于确定偏度值是否足够接近0(正太分布)。这里我们只对偏度值大于0.75的数据进行纠偏,偏度<0.75的数据是可以容忍的,现实中是不存在100%满足正太分布的数据。所以数据呈现轻微的偏斜是可以容忍的。
回归模型
ElasticNet(弹性网络)
- Ridge(岭回归)和Lasso(套索回归)都是常用的正则化的线性回归模型。它们分别使用L2和L1正则化。
- ElasticNet是Ridge(岭回归)和Lasso(套索回归)混合体,它同时使用L2和L1正则化,这种组合允许学习稀疏模型,其中包含了较少的像Lasso回归一样的非零权重,同时仍然保持Ridge的正则化特性。
- 当存在多个彼此相互关联的特征变量时ElasticNet非常有用。
- Skearn的ElasticNetCV类可用于通过交叉验证设置参数alpha(α)和l1_ratio(ρ)。
- ElasticNetCV:通过交叉验证选择最佳模型。
下面我们使用Skearn的ElasticNetCV来预测一下我们的目标变量,看看它效果如何。首先我们要对模型进行训练,并拟合出最佳的参数alpha和l1_ratio。
cv_model = ElasticNetCV(l1_ratio=[.1, .5, .7, .9, .95, .99, 1], eps=1e-3, n_alphas=100, fit_intercept=True,
normalize=True, precompute='auto', max_iter=2000, tol=0.0001, cv=6,
copy_X=True, verbose=0, n_jobs=-1, positive=False, random_state=0)
cv_model.fit(X_train, y_train)
print('最佳 alpha: %.8f'%cv_model.alpha_)
print('最佳 l1_ratio: %.3f'%cv_model.l1_ratio_)
print('迭代次数 %d'%cv_model.n_iter_)下面我们要在训练集和测试集上进行预测和评估,我们使用R^2和RMSE作为评估指标:
y_train_pred = cv_model.predict(X_train)
y_pred = cv_model.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred))
train_mse = mean_squared_error(y_train_pred, y_train)
test_mse = mean_squared_error(y_pred, y_test)
train_rmse = np.sqrt(train_mse)
test_rmse = np.sqrt(test_mse)
print('Train RMSE: %.4f' % train_rmse)
print('Test RMSE: %.4f' % test_rmse)这里的RMSE实际上是RMSLE(Root Mean Squared Logarithmic Error),因为我们的目标变量已经被对数化处理了。 这是一篇很好的文章,解释了RMSE和RMSLE之间的区别。
提取重要特征
训练完ElasticNetCV后我们可以从中提取对模型来说最重要的特征,也就是特征变量权重最大和最小的变量,我们取最大,最小各30个特征变量:
feature_importance = pd.Series(index = X_train.columns, data = cv_model.coef_)
n_selected_features = (feature_importance>0).sum()
print('{0:d} features, reduction of {1:2.2f}%'.format(
n_selected_features,(1-n_selected_features/len(feature_importance))*100))
feature_importance.sort_values().tail(30).plot(kind = 'bar', figsize = (12,5));我们看到特征变量GrLivArea的权重最大,GrLivArea表示“房屋地面以上面积”,可见房屋面积越大,房价也越高,这符合常理。下面我们再来看看权重值最小的30个变量:
feature_importance.sort_values().head(30).plot(kind = 'bar', figsize = (12,5));我们看到特征变量Condition2_PosN的权重最小,Condition2是个分类型变量,其中PosN表示“靠近停车场”。这是否意味着停车场附近会有噪声从而影响房价?
因为ElasticNet是Ridge(岭回归)和Lasso(套索回归)混合体,它同时使用L2和L1正则化,这种组合允许学习稀疏模型,那么我们看看有多少特征变量的权重为零,权重为零意味着这些特征对模型来说是无关紧要的。
feature_importance = pd.Series(index = X_train.columns, data = np.abs(cv_model.coef_))
zero_weight_features = (feature_importance==0).sum()
print('{0:d} 个权重为零的特征, 所在比例为 of {1:2.2f}%'.format(
zero_weight_features,(zero_weight_features/len(feature_importance))*100))![]()
可见有一半以上(58.91%)的特征对模型来说是无关紧要的,它们将被抛弃。
Xgboost
XGBoost全名叫(eXtreme Gradient Boosting)极端梯度提升,经常被用在一些Kaggle竞赛中,其效果显著。它是大规模并行boosted tree的工具,它是目前最快最好的开源boosted tree工具包,大家可以参考这篇博客。
下面我们创建基于4个不同参数的Xgboost模型,看看它们效果如何:
#使用默认参数
xgb_model1 = XGBRegressor()
xgb_model1.fit(X_train, y_train, verbose=False)
y_train_pred1 = xgb_model1.predict(X_train)
y_pred1 = xgb_model1.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred1, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred1))
train_mse1 = mean_squared_error(y_train_pred1, y_train)
test_mse1 = mean_squared_error(y_pred1, y_test)
train_rmse1 = np.sqrt(train_mse1)
test_rmse1 = np.sqrt(test_mse1)
print('Train RMSE: %.4f' % train_rmse1)
print('Test RMSE: %.4f' % test_rmse1)
xgb_model2 = XGBRegressor(n_estimators=1000)
xgb_model2.fit(X_train, y_train, early_stopping_rounds=5,
eval_set=[(X_test, y_test)], verbose=False)
y_train_pred2 = xgb_model2.predict(X_train)
y_pred2 = xgb_model2.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred2, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred2))
train_mse2 = mean_squared_error(y_train_pred2, y_train)
test_mse2 = mean_squared_error(y_pred2, y_test)
train_rmse2 = np.sqrt(train_mse2)
test_rmse2 = np.sqrt(test_mse2)
print('Train RMSE: %.4f' % train_rmse2)
print('Test RMSE: %.4f' % test_rmse2)
xgb_model3 = XGBRegressor(n_estimators=1000, learning_rate=0.05)
xgb_model3.fit(X_train, y_train, early_stopping_rounds=5,
eval_set=[(X_test, y_test)], verbose=False)
y_train_pred3 = xgb_model3.predict(X_train)
y_pred3 = xgb_model3.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred3, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred3))
train_mse3 = mean_squared_error(y_train_pred3, y_train)
test_mse3 = mean_squared_error(y_pred3, y_test)
train_rmse3 = np.sqrt(train_mse3)
test_rmse3 = np.sqrt(test_mse3)
print('Train RMSE: %.4f' % train_rmse3)
print('Test RMSE: %.4f' % test_rmse3)xgb_model4 = XGBRegressor(n_estimators=100, learning_rate=0.08, gamma=0, subsample=0.75,
colsample_bytree=1, max_depth=7, n_jobs=-1)
xgb_model4.fit(X_train,y_train)
y_train_pred4 = xgb_model4.predict(X_train)
y_pred4 = xgb_model4.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred4, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred4))
train_mse4 = mean_squared_error(y_train_pred4, y_train)
test_mse4 = mean_squared_error(y_pred4, y_test)
train_rmse4 = np.sqrt(train_mse4)
test_rmse4 = np.sqrt(test_mse4)
print('Train RMSE: %.4f' % train_rmse4)
print('Test RMSE: %.4f' % test_rmse4)我们可以看到第四个模型在测试集上的R^2成绩最好。并且我们采样默认参数的第一个XGboost模型的表现都要优于ElasticNet。
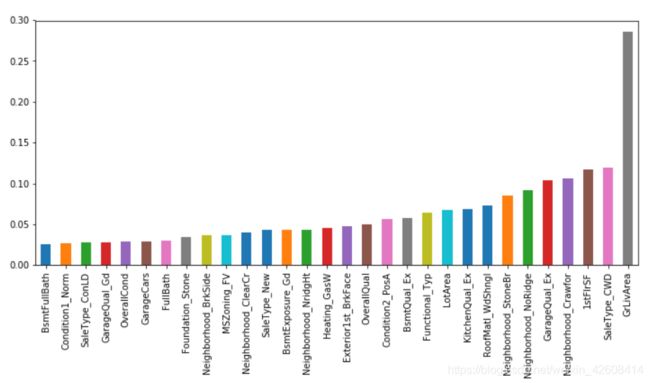
接下来我们查看一下最优模型xgb_model4 最重要的前30个特征变量
dic = xgb_model4.get_booster().get_fscore()
feature_importance = pd.DataFrame.from_dict(dic, orient='index', columns=['fscore'])
print('xgboost的特征数量:',len(feature_importance))
feature_importance_plot = feature_importance.sort_values(by="fscore" , ascending=False)[:30]
feature_importance_plot.plot(kind = 'bar', figsize = (12,5))
xgboost的特征数量是201个,可见也有一部分不重要的特征被舍弃了,其中最重要的前5个特征变量是LotArea、LotFrontage、MSSubClass、BsmtUnSF、TotalBsmtSF,它们都不在ElasticNet的前5个重要特征中,看来xgboost的重要特征的认定方法和ElasticNet完全不一样。
下面我们只取这201个特征,再用我们之前的最优模型xgb_model4再进行一下训练和预测,看看模型表现如何:
train_x=df[feature_importance.index]
train_y=df['SalePrice']
X_train, X_test, y_train, y_test = train_test_split(train_x, train_y, test_size = 0.2, random_state = 0)
xgb_model4.fit(X_train,y_train)
y_train_pred4 = xgb_model4.predict(X_train)
y_pred4 = xgb_model4.predict(X_test)
print('Train r2 score: ', r2_score(y_train_pred4, y_train))
print('Test r2 score: ', r2_score(y_test, y_pred4))
train_mse4 = mean_squared_error(y_train_pred4, y_train)
test_mse4 = mean_squared_error(y_pred4, y_test)
train_rmse4 = np.sqrt(train_mse4)
test_rmse4 = np.sqrt(test_mse4)
print('Train RMSE: %.4f' % train_rmse4)
print('Test RMSE: %.4f' % test_rmse4)最后我们发现,xgb_model4在测试集上的成绩提高到了0.9,又有一点小小的进步。
完整代码在这里下载