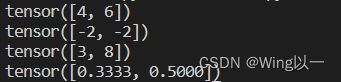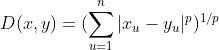【深度学习】1.张量tensor(下)
目录
五、张量的广播
六、张量的科学运算
1、逐点运算
2、规约运算
3、比较运算
七、张量的科学运算之线性代数
1、矩阵的形变及特殊矩阵的构造方法
2、矩阵的基本运算
3、矩阵的线性代数运算
4、矩阵分解运算
五、张量的广播
张量的广播特性允许不同形状的张量之间进行计算。一个或者多个张量通过隐式转化,转化为相同形状的两个张量,完成计算。
- 同形状张量计算
- 标量和任意形状的张量
- 相同维度、不同形状的张量之间计算:不同形状(在一个分量上取值不同),但该分量上取值为1即可广播。(多个分量上取值均不相同,但都有存在1的情况,也可以广播。例(1,3)(3,1))
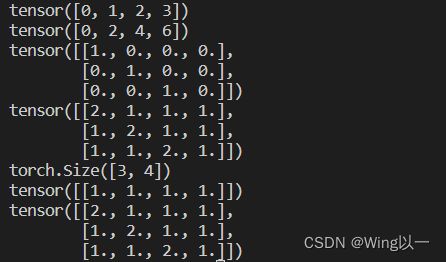
t1=torch.arange(4)
print(t1)
print(t1+t1)
t2=torch.eye(3,4)
print(t2)
print(t2+1)
print(t2.shape)
t21=torch.ones(1,4)
print(t21)
print(t21+t2)通过三维来推导,如何判断高维张量是否可以广播?
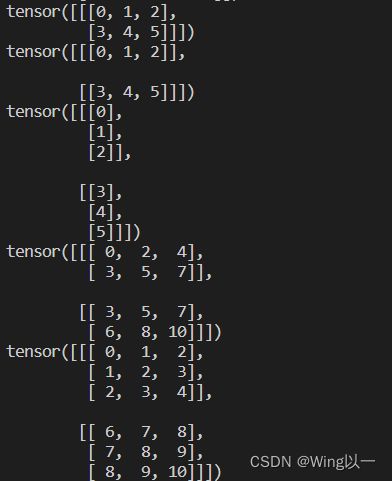
t3=torch.arange(6).reshape(1,2,3)
t4=torch.arange(6).reshape(2,1,3)
t5=torch.arange(6).reshape(2,3,1)
print(t3)
print(t4)
print(t5)
print(t3+t4)
print(t4+t5)- 不同维度的张量广播计算
低维张量升维(将更高维度方向填充为1),来同高维张量进行广播计算。
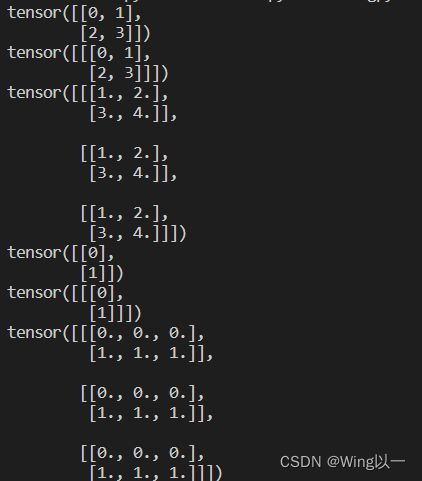
t1=torch.arange(4).reshape(2,2)
print(t1)
print(t1.reshape(1,2,2))
t2=torch.ones(3,2,2)
print(t1+t2)
t3=torch.arange(2).reshape(2,1)
print(t3)
print(t3.reshape(1,2,1))
t4=torch.zeros(3,2,3)
print(t3+t4)六、张量的科学运算
数学运算的分类:
- 逐点运算(Pointwise Ops)
- 规约运算(Reduction Ops)
- 比较运算(Comparison Ops)
- 谱运算(Spectral Ops)
- BLAS和LAPACK运算:线性代数程序集和线性代数包
- 其它运算
1、逐点运算
- 基本数学运算
| 函数 | 描述 |
| torch.add(t1,t2 ) | t1、t2两个张量逐个元素相加,等效于t1+t2 |
| torch.sub(t1,t2) | t1、t2两个张量逐个元素相减,等效于t1-t2 |
| torch.mul(t1,t2) | t1、t2两个张量逐个元素相乘,等效于t1*t2 |
| torch.true_divide(t1,t2) | t1、t2两个张量逐个元素相除,等效于t1/t2 |
t1=torch.tensor([1,2])
t2=torch.tensor([3,4])
print(torch.add(t1,t2))
print(torch.sub(t1,t2))
print(torch.mul(t1,t2))
print(torch.true_divide(t1,t2))- 数值调整函数
| 函数 | 描述 |
| torch.abs(t) | 返回绝对值 |
| torch.ceil(t) | 向上取整 |
| torch.floor(t) | 向下取整 |
| torch.round(t) | 四舍五入取整 |
| torch.neg(t) | 返回相反的数 |
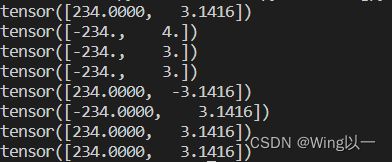
t1=torch.tensor([-234,3.1415926])
print(torch.abs(t1))
print(torch.ceil(t1))
print(torch.floor(t1))
print(torch.round(t1))
print(torch.neg(t1))
print(t1) #以上操作并不改变t1本身
print(torch.abs_(t1))
print(t1) #以上操作后加_可直接对t1做调整- 常用科学计算
| 数学运算函数 | 数学公式 | 描述 |
| 幂运算 | ||
| torch.exp(t) | 返回以e为底、t中元素为幂的张量 | |
| torch.expm1(t) | 对张量中的所有元素计算exp(x) - 1 | |
| torch.exp2(t) | 逐个元素计算2的t次方 | |
| torch.pow(t,n) | 返回t的n次幂 | |
| torch.sqrt(t) | 返回t的平方根 | |
| torch.square(t) | 返回输入的元素平方 | |
| 对数运算 | ||
| torch.log10(t) | 返回以10为底的t的对数 | |
| torch.log(t) | 返回以e为底的t的对数 | |
| torch.log2(t) | 返回以2为底的t的对数 | |
| torch.log1p(t) | 返回一个加1的自然对数的输入数组 | |
| 三角函数运算 | ||
| torch.sin(t) | 三角正弦 | |
| torch.cos(t) | 余弦 | |
| torch.tan(t) | 逐元素计算切线 | |
tensor的大部分科学计算只能作用于tensor对象。
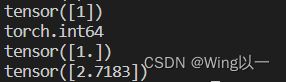
print(torch.pow(torch.tensor(2),2))tensor的大部分科学运算具有一定的静态性。(输出为浮点型张量的函数一般要求输入也为浮点型张量,而非整形张量)
t=torch.arange(1,2)
print(t)
print(t.dtype)
t1=t.float()
print(t1)
print(torch.exp(t1))torch.log1p(t) 与torch.expm1(t),这一对函数是互相为解的。
- 排序运算:sort
t=torch.tensor([1,4,5,3,2])
print(torch.sort(t))
print(torch.sort(t,descending=True))2、规约运算
- 统计分析函数
| 函数 | 描述 |
| torch.mean(t) | 返回张量均值 |
| torch.var(t) | 返回张量方差 |
| torch.std(t) | 返回张量标准差 |
| torch.var_mean(t) | 返回张量方差和均值 |
| torch.std_mean(t) | 返回张量标准差和均值 |
| torch.max(t) | 返回张量最大值 |
| torch.argmax(t) | 返回张量最大值索引 |
| torch.min(t) | 返回张量最小值 |
| torch.argmin(t) | 返回张量最小值索引 |
| torch.median(t) | 返回张量中位数 |
| torch.sum(t) | 返回张量求和结果 |
| torch.logsumexp(t) | 返回张量各元素求和结果,适用于数据量较小的情况 |
| torch.prod(t) | 返回张量累乘结果 |
| torch.dist(t1, t2) | 计算两个张量的闵式距离,可使用不同范式 |
| torch.topk(t) | 返回t中最大的k个值对应的指标 |
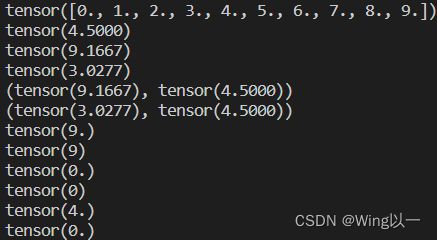
t=torch.arange(10).float()
print(t)
print(torch.mean(t))
print(torch.var(t))
print(torch.std(t))
print(torch.var_mean(t))
print(torch.std_mean(t))
print(torch.max(t))
print(torch.argmax(t))
print(torch.min(t))
print(torch.argmin(t))
print(torch.median(t))
print(torch.prod(t))dist计算明可夫斯基距离
t1=torch.tensor([1.0,2,3])
t2=torch.tensor([4,5.0,6])
print(torch.dist(t1,t2,2)) #p=2计算欧式距离
print(torch.dist(t1,t2,1)) #p=1计算街道距离- 规约运算的维度
对于高维张量,可以指定某维度进行规约运算。
t1=torch.arange(24).float().reshape(2,3,4)
print(t1)
print(torch.sum(t1,dim=0)) #两个矩阵对应位置元素相加求和
print(torch.sum(t1,dim=1)) #两个矩阵分别按列求和
print(torch.sum(t1,dim=2)) #两个矩阵分布按行求和- 二维张量的排序
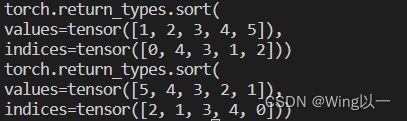
t23=torch.randn(2,3)
print(t23)
print(torch.sort(t23))
print(torch.sort(t23,dim=1,descending=True)) #按行降序排序3、比较运算
| 函数 |
描述 |
| torch.eq(t1, t2) | 比较t1、t2各元素是否相等,等效== |
| torch.equal(t1, t2) | 判断两个张量是否是相同的张量 |
| torch.gt(t1, t2) | 比较t1各元素是否大于t2各元素,等效> |
| torch.lt(t1, t2) | 比较t1各元素是否小于t2各元素,等效< |
| torch.ge(t1, t2) | 比较t1各元素是否大于或等于t2各元素,等效>= |
| torch.le(t1, t2) | 比较t1各元素是否小于等于t2各元素,等效<= |
| torch.ne(t1, t2) | 比较t1、t2各元素是否不相同,等效!= |
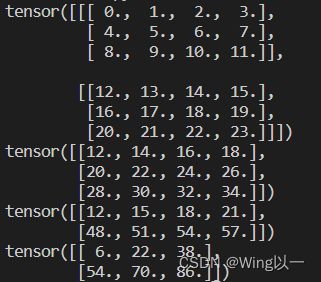
t1=torch.tensor([1.0,2,3])
t2=torch.tensor([1,2.0,4])
print(torch.eq(t1,t2))
print(torch.equal(t1,t2))
print(torch.gt(t1,t2))
print(torch.lt(t1,t2))
print(torch.ge(t1,t2))
print(torch.le(t1,t2))
print(torch.ne(t1,t2))七、张量的科学运算之线性代数
BLAS(Basic Linear Algeria Subprograms)和LAPACK(Linear Algeria Package)模块提供了完整的线性代数基本方法,简单分类,具体包括:
- 矩阵的形变及特殊矩阵的构造方法:包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等;
- 矩阵的基本运算:包括矩阵乘法、向量内积、矩阵和向量的乘法等,当然,此处还包含了高维张量的基本运算,将着重探讨矩阵的基本运算拓展至三维张量中的基本方法;
- 矩阵的线性代数运算:包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等;
- 矩阵分解运算:特征分解、奇异值分解和SVD分解等。
1、矩阵的形变及特殊矩阵的构造方法
| 函数 | 描述 |
| torch.t(t) | t转置 |
| torch.eye(n) | 创建包含n个分量的单位矩阵 |
| torch.diag(t) | 以t中各元素,创建对角矩阵 |
| torch.triu(t) | 取矩阵t中的上三角矩阵 |
| torch.tril(t) | 取矩阵t中的下三角矩阵 |
t1=torch.arange(2,8).reshape(2,3).float()
print(t1)
print(torch.t(t1))
print(torch.diag(t1))
print(torch.triu(t1))
print(torch.tril(t1))2、矩阵的基本运算
| 函数 | 描述 |
| torch.dot(t1, t2) | 计算t1、t2张量内积(仅一维) |
| torch.mm(t1, t2) | 矩阵乘法 |
| torch.mv(t1, t2) | 矩阵乘向量 |
| torch.bmm(t1, t2) | 批量矩阵乘法 |
| torch.addmm(t, t1, t2) | 矩阵相乘后相加 |
| torch.addbmm(t, t1, t2) | 批量矩阵相乘后相加 |
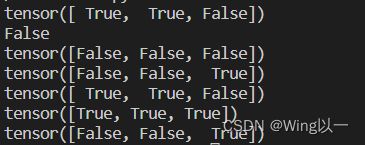
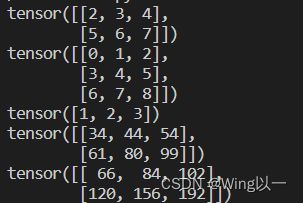
t1=torch.arange(2,8).reshape(2,3)
print(t1)
t2=torch.arange(9).reshape(3,3)
print(t2)
print(torch.mm(t1,t2)) #矩阵乘法m*n和n*l的矩阵
t3=torch.arange(1,4)
print(t3)
print(torch.mv(t1,t3)) #矩阵和向量相乘(矩阵列数与向量元素个数相同)
print(torch.mm(t1,t3.reshape(3,1)).flatten()) #可以看作先将向量转化为列向量后再相乘
线性回归的求解,通常情况下需将向量转化为列向量,再进行计算。在pytorch里,我们均可以使用mv函数来完成。
t1=torch.arange(2,8).reshape(2,3)
print(t1)
t2=torch.arange(9).reshape(3,3)
print(t2)
t3=torch.arange(1,4)
print(t3)
print(torch.addmm(t3,t1,t2))
print(torch.addmm(t3, t1, t2, beta = 0, alpha = 2))addmm函数结构:addmm(input, mat1, mat2, beta=1, alpha=1)
输出结果:beta * input + alpha * (mat1 * mat2)
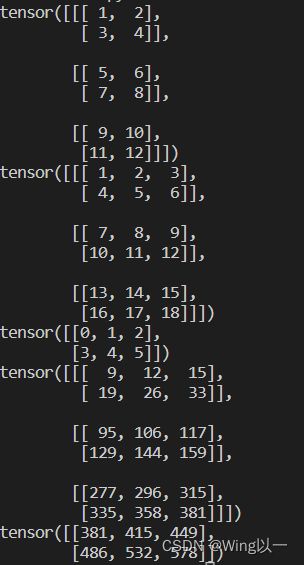
t3=torch.arange(1,13).reshape(3,2,2)
print(t3)
t4=torch.arange(1,19).reshape(3,2,3)
print(t4)
t = torch.arange(6).reshape(2, 3)
print(t)
print(torch.bmm(t3,t4)) #包含的矩阵个数要相同,内部满足矩阵乘法m*n和n*l
print(torch.addbmm(t, t3, t4)) #批量矩阵相乘后相加
3、矩阵的线性代数运算
| 函数 | 描述 |
| torch.trace(A) | 矩阵的迹 |
| matrix_rank(A) | 矩阵的秩 |
| torch.det(A) | 计算矩阵A的行列式 |
| torch.inverse(A) | 矩阵求逆 |
| torch.lstsq(A,B) | 最小二乘法 |
t=torch.tensor([[1.0,2,3],[3,4,5],[2,4,6]])
print(t)
print(torch.trace(t))
print(torch.matrix_rank(t))
print(torch.det(t)) #行列式计算要求二维张量行列数一致(为正方形)用矩阵求解齐次线性方程组
Ax=B的求解,![]()
A=torch.tensor([[1.0,1],[3,1]])
B=torch.tensor([4.0,10])
x=torch.mv(torch.inverse(A),B)
print(x)![]()
最终的线性方程为![]()
4、矩阵分解运算
矩阵的分解也是矩阵运算中的常规计算,矩阵分解也有很多种类,常见的例如QR分解、LU分解、特征分解、SVD分解等。
- 特征分解
特征分解中的矩阵分解形式如下:
![]() 其中,
其中,![]() 和
和![]() 互为逆矩阵,并且
互为逆矩阵,并且![]() 的列就是
的列就是![]() 的特征值所对应的特征向量,而
的特征值所对应的特征向量,而![]() 为矩阵
为矩阵![]() 的特征值按照降序排列组成的对角矩阵。
的特征值按照降序排列组成的对角矩阵。
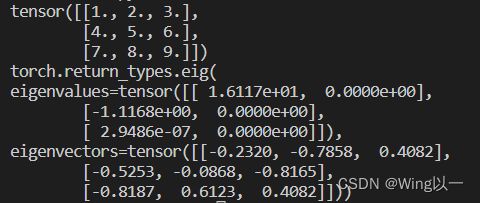
A = torch.arange(1, 10).reshape(3, 3).float()
print(A)
print(torch.eig(A,eigenvectors=True))eigenvalues表示特征值向量,即A矩阵分解后的Λ矩阵的对角线元素值,并按照又大到小依次排列,eigenvectors表示A矩阵分解后的Q矩阵。
特征值,可简单理解为对应列在矩阵中的信息权重,如果该列能够简单线性变换来表示其他列,则说明该列信息权重较大,反之则较小。(此例中,前两个向量信息权重较大)
由于特征分解只能作用于方阵,而大多数实际情况下矩阵行列数未必相等,此时要进行类似的操作就需要采用和特征值分解思想类似的奇异值分解(SVD)。
- 奇异值分解
奇异值分解是特征值分解在奇异矩阵上的推广形式,它将一个维度为m×n的奇异矩阵A分解成三个部分 : ![]()
其中U、V是两个正交矩阵,其中的每一行(每一列)分别被称为左奇异向量和右奇异向量,他们和∑中对角线上的奇异值相对应,通常情况下我们只需要保留前k个奇异向量和奇异值即可,其中U是m×k矩阵,V是n×k矩阵,∑是k×k的方阵,从而达到减少存储空间的效果,即:
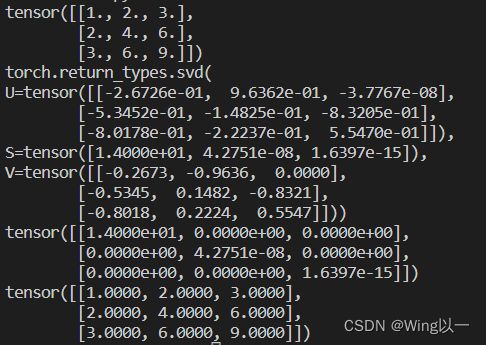
A = torch.tensor([[1.,2,3],[2.,4,6],[3,6,9]])
print(A)
print(torch.svd(A))
'''验证SVD'''
AU, AS, AV = torch.svd(A)
print(torch.diag(AS))
print(torch.mm(torch.mm(AU,torch.diag(AS)),AV.t()))可根据svd输出结果对C进行降维,此时C可只保留第一列(后面的奇异值过小),即k=1 。