Towards Class-Oriented Poisoning Attacks Against Neural Networks 论文笔记

#论文笔记#

1. 论文信息

论文名称	Towards Class-Oriented Poisoning Attacks Against Neural Networks
作者	Bingyin Zhao
会议/出版社	WACV 2022
pdf	在线pdf
代码	无

基于类别的 availability attacks，不同于原本的 availability attacks 只考虑降低模型的整体准确率，本文还考虑了降低特定类的准确率或迫使模型将其他类都预测为目标类。

2. introduction

本文提出了面向类别的 availability attacks，通过梯度优化的方法生成 posion data。使用该 posion data 训练出的模型在特定类别上的准确率发生异常。

• availability attacks 的优化目标，bi-level optimization problem

  $\underset{{\mathcal{D}}_p}{\mathrm{argmax}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{\text{val }}}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y,{\theta }^{\ast }\right]$
  S.t. ${\theta }^{\ast }\in \underset{{\theta }^{\ast }\in \Theta }{\mathrm{argmin}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{tr}\cup {\mathcal{D}}_p}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y,\theta \right]$,

• 威胁模型

  • 攻击者知道，算法结构，超参数以及训练数据集
  • 攻击者可以对训练数据集注入有毒数据并且修改标签

3. method

两种攻击方式：

Class-Oriented availability attacks 可以为两种：

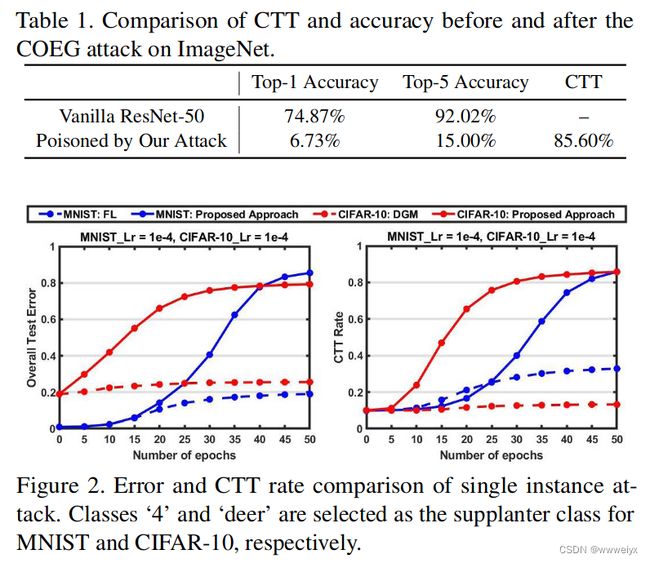
COEG class-oriented error-generic

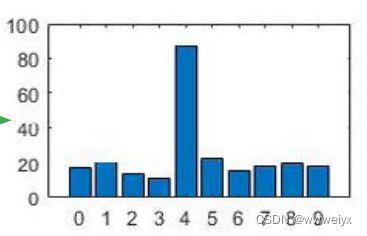
目标：让模型将所有的输入都分类成目标类（supplanter class）

目标函数：$\underset{{\mathcal{D}}_p}{\mathrm{argmax}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{\text{val }}}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y,{\theta }^{\ast }\right]$
s.t. ${\theta }^{\ast }\in \underset{{\theta }^{\ast }\in \Theta }{\mathrm{argmin}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{tr}\cup {\mathcal{D}}_p}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y_s,\theta \right]$,

$y_s$ 表示目标类

COES class-oriented error-specific

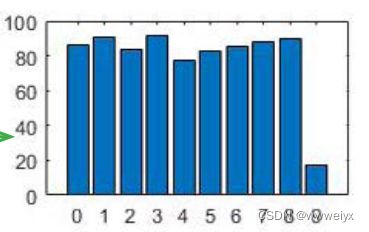
目标：降低 victim classes 的准确率，保持 non-victim classes(其他类) 的准确率不变

目标函数：$\underset{{\mathcal{D}}_p}{\mathrm{argmax}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{val}}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y_v,{\theta }^{\ast }\right]$
s.t. ${\theta }^{\ast }\in \underset{{\theta }^{\ast }\in \Theta }{\mathrm{argmin}}{\sum }_{(\mathbf{x},y)\in {\mathcal{D}}_{tr\cup {\mathcal{D}}_p}}L\left[{\mathcal{F}}_{{\theta }^{\ast }}(\mathbf{x}),y_{\bar{v}},\theta \right]$,

$y_v$ 表示 victim classes，$y_{\bar{v}}$ 表示 non-victim classes

两种攻击方式的训练方法

• COEG Attack

  目标函数：

  • $L=\lambda \cdot L_{f_{y_s}}-L_{f_{y_o}}$
  • $L_{f_{y_s}}=f_{y_s}(\mathbf{x})$
  • $f_{y_k}$ as the corresponding logit to the categorical label $y_k$
  • $f_{y_o}(\mathbf{x})$ is the logit output of the groundtruth class

  poisoned image $x_p$

  ${\mathbf{x}}_{\mathbf{p}}={\mathbf{x}}_{\mathbf{o}}-ϵ\cdot \mathrm{sign}\left({\nabla }_{{\mathbf{x}}_o}\left(\lambda \cdot L_{f_{y_s}}-L_{f_{y_o}}\right)\right)$

  算法流程
  

• COES Attack

  COES 既要降低目标类的准确率，又要保持其他类的准确率。

  加毒的过程分为：

  1. 在每一类中选取相同的数量的图片
  2. 通过算法2提升或者减少每幅图像与 label 信息对应的特征信息
  3. 改变目标类的标签

  目标函数：

  $L=\{\begin{array}{ll}\lambda \cdot L_{f_{y_s}}-L_{f_{y_o}},& \text{ if }{x}_o\in {\mathcal{C}}_v\\ L_{f_{y_o}},& \text{ otherwise }\end{array}$

  poisoned image $x_p$

  $\{\begin{array}{ll}{x}_o-ϵ\cdot \mathrm{sign}\left({\nabla }_{x_o}\left(\lambda \cdot L_{f_{y_s}}-L_{f_{y_o}}\right)\right),& \text{ if }{x}_o\in {\mathcal{C}}_v\\ x_o+ϵ\cdot \mathrm{sign}\left({\nabla }_{x_o}\left(L_{f_{y_o}}\right)\right),& \text{ otherwise }\end{array}$

  算法2：

4. experiments

评价指标：

• Change-to-Target (CTT)：其他类被分到目标类的比例
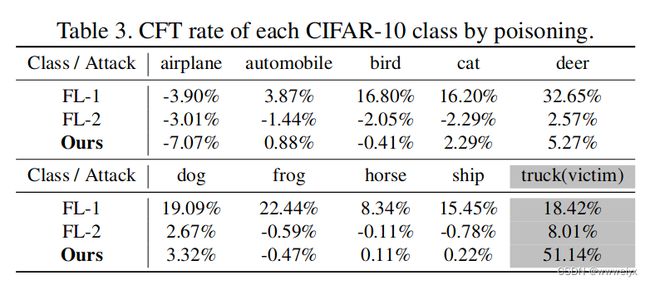
• Change-from-Target (CFT) ：目标类被错误分类的比例

数据集一
MNIST

数据集二
CIFAR-10

数据集三
ImageNet-ILSVRC2012

• COEG 在三个数据集上的实验结果：
  

• COES 在 cifar10 上的实验结果：