零基础讲解PCA降维算法原理推导

降维是一种对特征进行压缩的过程，能将特征中的重复冗余特征删除，保留少数最有效的特征。本文从0开始讲解PCA线性降维的推导过程。
注：虽说是零基础，但完整推导必备知识点有拉格朗日乘子法，简单的矩阵求导，矩阵特征分解，若不会也没关系，知道大概怎么一回事就行。

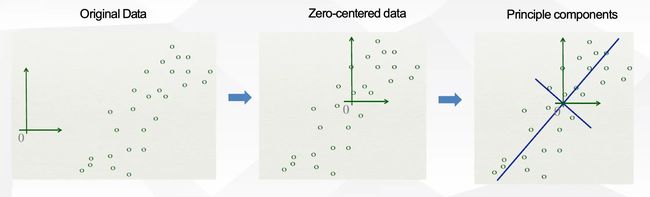
PCA降维的直观理解

原始数据为$X=(x_1,x_2,\cdots ,x_n)\in {\mathbb{R}}^{D\times N}$，$D$是样本的维度，$N$是样本的数量。

我们目的是通过PCA降低样本维度，得到新的低维数据点$X=(z_1,z_2,\cdots ,z_N)\in {\mathbb{R}}^{D^{\prime }\times N}$，其中$D^{\prime }\ll D$。

PCA算法的直观解释：

• 通过PCA算法，可以得到1个新的坐标系，包含$D^{\prime }$个标准正交（单位且正交）的坐标轴$W=(w_1,w_2,\cdots ,w_{D^{\prime }})$
• 将原始数据映射到新的坐标系$W$中，那么每个数据的维度都是$D^{\prime }$了

因此PCA算法的关键问题就是如何寻找一个新的坐标轴，能保证映射后的数据与原始数据尽量的接近，尽量少的丢失信息，而且尽量要把维度降低下来。

当然，少丢失信息和维度降低肯定不能两全，维度越低丢失的信息就一定会更多，维度越高丢失的信息就越少，因此需要在这二者中进行一个权衡。

下面就开始推导如何得到这个新的坐标轴$W$。

目标函数：最小化重建误差

任何机器学习算法都有损失函数，PCA也有一个损失函数，这个损失函数描述了降维后的数据还原回降维前的数据时，与降维前数据之间的误差，因此也叫重建误差。

之前我们说了，我们目标是求一个标准正交的坐标轴$W$，那么就有$w_i^T{w}_j=0(i\ne j)$，$w_i^T{w}_i=1(或||w_i||=1)$。

那么PCA编码（降维）的过程就是将原始数据映射到这个新的坐标轴中，第$i$个低维数据$z_i$的计算公式为$z_i=W^T{x}_i$，其中的第$j$个分量为$z_{i,j}=W_j^T{x}_i$，新坐标系中每个坐标轴可以得到低维数据的一个分量，$D^{\prime }$个坐标轴得到$D^{\prime }$个分量。可以参考同济线代课本关于这部分的知识：

解码过程就是把上述过程反过来，通过低维数据坐标以及坐标轴，得到原始的数据。由于坐标轴$W$是标准正交的，因此$W^{-1}=W^T$，很容易得到重建数据为${\hat{x}}_i={\sum }_{i=1}^{D^{\prime }}{z}_{i,j}{w}_i=W{z}_i$（也可以根据上图中的公式直接得到）。

那么我们的目标就是将重建误差最小化：
$$\underset{W\in {\mathbb{R}}^{D\times D^{\prime }}}{\min }\sum _{i=1}^N{\Vert x_i-W{z}_i\Vert }_2^2$$
$||a-b|{|}_2^2$表示L2距离的平方，待求的参数是坐标轴$W$。

将上述公式继续化简：
$$\begin{array}{rl}\sum _{i=1}^N{\Vert x_i-W{z}_i\Vert }^2& =\sum _{i=1}^N(x_i-W{z}_i{)}^T(x_i-W{z}_i)\\ & =\sum _{i=1}^N(x_i^T{x}_i-x_i^T(W{z}_i)-(W{z}_i{)}^T{x}_i+z_i^T{W}^{T}W{z}_i)\\ & =\sum _{i=1}^N(z_i^T{z}_i-2z_i^T{W}^T{x}_i+const)\\ & =-\sum _{i=1}^N{z}_i^T{z}_i+const\end{array}$$
解释一下上述公式，${\Vert x_i-W{z}_i\Vert }^2$是向量的模长的平方，也就是每个元素平方的乘积，第一步就是转化成向量的形式，第二步先把转置放进去，然后乘法分配律乘开来，第三步中用到了$W^{T}W=E$，且$x_i^T(W{z}_i)$是个常数，转置也是常数，所以合并起来就是2，然后$x_i^T{x}_i$是个与优化目标无关的常数，因此不用管。最后一步用到了$z_i=W^T{x}_i$。

经过上述步骤化简，我们得到了最终的优化目标：
$$-\sum _{i=1}^N{z}_i^T{z}_i$$
我们要让上述值最小，也就是让下式最大：
$$\sum _{i=1}^N{z}_i^T{z}_i$$
$z_i^T{z}_i$是降维后第$i$个数据的方差（假定样本已经中心化了），那么对PCA可以进一步直观的理解为：

• 寻找一个新的坐标轴，让原始数据投影到这个新的坐标轴后，数据（第一个维度）的方差最大
• 如果能找到，继续寻找下一个与之前坐标轴正交的坐标轴，同时也要使数据（第二个维度）的方差最大（因为每个坐标轴是不相关的，除了相互正交，各自不影响）
• 如果能找到一些这样的坐标轴（方向向量），我们就称它们为主成分，通过这些主成分我们能精确的描述原始数据

目标函数的计算

我们目前要求解的是一个最优的$W$：
$$\underset{W}{\max }\sum _{i=1}^N{z}_i^T{z}_i=\underset{W}{\max }tr(Z{Z}^T)=\underset{W}{\max }tr(W^{T}X{X}^{T}W)$$
$tr(X)$表示矩阵$X$的迹，也就是对角线元素求和，可以拿笔画一画，二者是一致的。再另$S=X{X}^T$，上式转化为：
$$\underset{W}{\max }tr(W^{T}SW)$$
寻找一个$W\in {\mathbb{R}}^{D\times D^{\prime }}$，使得上式成立，不过要注意，还有一个约束条件：$s.t.W^{T}W=I$，矩阵$W$是坐标系，要求单位且正交。

带约束的优化问题，使用拉格朗日乘子法。

由于目标函数是求迹的最大值，对角线元素的最大值，我们可以分解为对每个对角线元素求最大值，因为每个对角线上的每个元素只与一个$w$有关，而各个$w$除了正交都是不相关的，因此可以单独考虑。

坐标系中的第一个方向向量$w_1$，目标函数为$J=tr(w_1^{T}S{w}_1)=w_{1}S{w}_1$，约束为$w_1^T{w}_1=1$，引入拉格朗日函数

• $L={\mathbf{w}}_1^T\mathbf{S}{\mathbf{w}}_1-{\lambda }_1\left({\mathbf{w}}_1^T{\mathbf{w}}_1-1\right)$
• $\frac{\partial L}{\partial {\mathbf{w}}_1}=2\mathbf{S}{\mathbf{w}}_1-2{\lambda }_1{\mathbf{w}}_1=0$，
• 那么$\mathbf{S}{\mathbf{w}}_1={\lambda }_1{\mathbf{w}}_1$，即${\mathbf{w}}_1$是$\mathbf{S}$的特征向量。
• 目标函数$J={\mathbf{w}}_1^T\mathbf{S}{\mathbf{w}}_1={\mathbf{w}}_1^T{\lambda }_1{\mathbf{w}}_1={\lambda }_1$

然后考虑第二个方向向量$w_2$，按照上述算法同样计算，能得到$w_2$也是$S$的特征向量，目标函数为$J={\lambda }_1+{\lambda }_2$。

依次计算下去，每个坐标轴都是$S$的特征向量，定义$w_d$是$S$的第$d$大特征向量，目标函数为$J={\sum }_i{\lambda }_i$。

原本我们还需要考虑每个投影坐标轴之间相互正交，现在求出来的坐标轴就是特征向量，一个可逆矩阵的特征向量必定正交，因此我们此时无需再考虑那个条件。（$S$矩阵不一定可逆，因此有基于SVD的PCA）

至此，我们求出了最优的投影坐标轴，并且得到了每个坐标轴所包含的信息量（该坐标轴对应的特征值大小），选的坐标轴越多，所包含的信息越多，维度也越高，选的坐标越少，所包含的信息也越少，维度也越低。

PCA算法流程

输入：$X=(x_1,x_2,\cdots ,x_N)$，低维度空间的维度：$D^{\prime }$

算法流程：

• 计算数据的平均值：$\overline{x}=\frac{1}{N}{\sum }_{j=1}^N{x}_j$

• 数据中心化：$x_i=x_i-\overline{x}$（为了保证变化后的$z_i$是中心化的，上述推导用到了$z_i$是中心化的数据）

• 计算协方差矩阵：$S=X{X}^T$

• 对$S$做特征分解

• 得到最大的$D^{\prime }$个特征值对应的特征向量：$w_1,w_2,\cdots ,w_{D^{\prime }}$

输出：$W=(w_1,w_2,\cdots ,w_{D^{\prime }})$

基于SVD的PCA

在上述PCA算法中，我们要计算协方差矩阵$S=X{X}^T\in {\mathbb{R}}^{D\times D}$，若原始维度就有$10^4$，那这个矩阵有$10^8$个元素，运算量十分巨大。而且还要求$S$是可逆矩阵，虽然可能90%的情况下$S$都会是可逆的，但如果这个矩阵就是不可逆，那我们就没法通过上述方法进行降维了。

此时我们需要用到奇异值分解（SVD）方法，SVD的有一些实现能快速获得矩阵的最大$D$个特征值对应的特征向量，与我们的原始目的一致。

这一部分就不详细讲，有兴趣的可以去看看怎么分解，与降维的关系已经不大了。

基于SVD的PCA算法流程

输入：$X=(x_1,x_2,\cdots ,x_N)$，低维度空间的维度：$D^{\prime }$

算法流程：

• 计算数据的平均值：$\overline{x}=\frac{1}{N}{\sum }_{j=1}^N{x}_j$
• 奇异值分解$\mathbf{X}={\mathbf{U}}_{D\times D}{\mathbf{\Sigma }}_{D\times N}{\mathbf{V}}_{N\times N}^{\mathrm{T}}$
• $D^{\prime }$个奇异值对应的左奇异向量：$u_1,u_2,\cdots ,u_{D^{\prime }}$

输出：$U=(u_1,u_2,\cdots ,u_{D^{\prime }})$

PCA算法中参数的指定

之前推到中看到每个坐标轴方向对应的特征值实际上能表示包含的信息量，因此可以通过这个特征值判断所选择的参数保留了多少原始信息，然后通过一个重建阈值来选择最小的降维维度：
$$\sum _{d=1}^{D^{\prime }}{\lambda }_d/\sum _{d=1}^D{\lambda }_d\ge t(\mathrm{e}.\mathrm{g}.\text{ 方差的85\%) }$$
PCA中保留的信息量一般随着维度增加上升的非常快，因此一般都能降到很低维。

非线性降维KPCA

PCA进阶之KPCA可以看下一篇文章
KPCA非线性降维原理推导