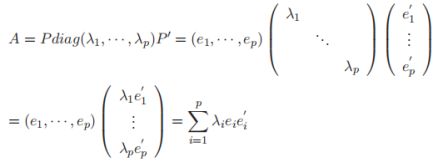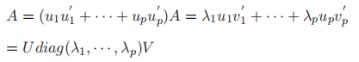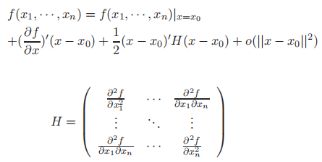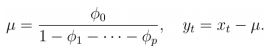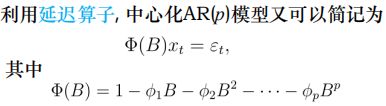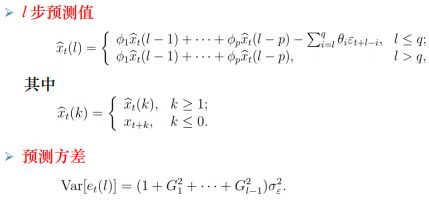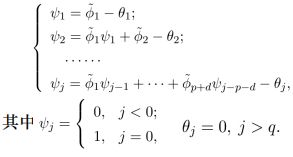【应用统计】【课程笔记】 线性代数、概率统计、多元回归、时间序列

本文为《应用统计方法》复习笔记，用于总结知识点和框架，分为线性代数、概率统计、多元回归和时间序列等，仅供参考和交流，参考书籍为《高等计量经济学》。

博客推荐：

• AI算法工程师手册 华校专：数学学习、统计基础、深度学习

• 我是8位的：单变量微积分、多变量微积分、线性代数、概率

---

第一部分 线性代数

几何解释总结

1、a在b上的投影、随机变量y在随机变量x上的投影。

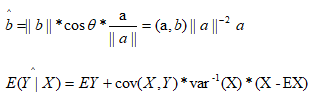
2、相关系数 = 夹角余弦（L2空间）
3、正交分解定理：
估计量（在空间上的投影）、残差（平面外一点到平面的距离）
4、行列式：面积/体积（平行四边形的面积、平行六面体的体积）
$Jaccobi$行列式：面积的比值（$dxdy—>dudv$）
5、正交阵：旋转
6、投影阵：βx为y在子空间$S(1,x)$上的线性投影。

第一章 线性空间

一、欧氏空间、线性空间、内积空间

欧氏空间、线性空间（由一组向量生成的线性空间）、内积空间（定义内积和运算）[1]

二、线性空间的基、维数、秩

基（基向量）、维数（线性无关线性向量组中向量个数）、秩（极大线性无关向量组）

第二章 矩阵基本知识

一、矩阵运算

1、转置：AB的转置，等于B的转置乘以A的转置。
2、逆运算：AB的逆，等于B的逆乘以A的逆。
3、转置+逆：A的转置的逆，等于A的逆的转置。

二、分块矩阵运算

几个重要公式：
1、小尾巴公式要诀：先是自己，然后减去：顺时针转，对角线取逆
2、小尾巴取逆公式要诀：先是自己的逆，然后加上：顺时针转，从自己的逆开始到自己的逆结束，遇到同对角线取逆还加小尾巴
3、$A^{-1}$取逆公式要诀：左上右下对角线：自己取逆加小尾巴，右上左下对角线：左乘同行取逆，右乘同列取逆，只保留一个小尾巴（相等），再加负号

三、矩阵的数字特征

1、$Jacobian$行列式
几何解释[2]：代表$xy$平面上的面积微元与uv平面上的面积微元的比值。

2、行列式的性质：$|A||B|=|AB|$
对角块行列式乘积：$|A|=|A_{11}||A_{22.1}|$

3、特征根和特征向量[3]
（1）定义（几何解释）[4]：①对于给定矩阵A，寻找一个常数λ和非零向量x，使得向量x被矩阵A作用后所得的向量Ax与原向量x平行，并且满足Ax=λx。②如果把矩阵看作是运动，那么特征值就是运动的速度，特征向量就是运动的方向。
（2）施密特正交化：求单位正交特征向量。

第三章 几类特殊矩阵

一、特征值分解（谱分解）

1、主成分分析（PCA）[4]：（1）最大化投影后数据的方差(让数据更分散)；（2）最小化投影造成的损失。
2、特征值分解、单位正交化实现主成分分析[5]：（1）通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量；（2）选择特征值最大（即方差最大）的k个特征所对应的特征向量组成的矩阵，即将数据矩阵转换到新的空间当中，实现数据特征的降维。
补充：方差分解、特征值分解、因子旋转实现因子分析

二、奇异值分解（SVD）

数学解释[6]：求解3个矩阵的过程，即求解特征值和特征向量的过程。

三、Hessian矩阵、泰勒公式展开

$Hessian$矩阵：二阶偏导[7]

四、投影阵

若矩阵A既是对称矩阵，又是幂等矩阵，则称A为投影矩阵。

第四章 二次型

对于二次型矩阵[8]，都是对称矩阵，所以特征值分解[9]总可以得到正交矩阵与对角阵。

第五章 矩阵的特殊运算和矩阵微商

一、矩阵拉直

二、矩阵叉积

三、矩阵微商

1、一个变量对一个向量求导：梯度
2、一个矩阵对一个向量求导：先把矩阵拉直，再转置

---

第二部分 概率统计

第一章 随机变量和随机向量的数字特征

一、映射 傅里叶变换 拉普拉斯变换

函数：数->数 泛函：函数->数 集函：集合->函数

二、二项分布、泊松分布、均匀分布、正态分布

三、直方图

做数据分析，要把频数图改成直方图，且数据不要放在分组线上

四、随机向量的分布及随机向量函数的分布

1、联合分布、边缘分布、条件分布
2、中位数
①中位数具有稳健性。
②方差和标准差：不对称用中位数，对称用均值。

五、随机向量的数字特征

1、相关系数和相关系数矩：
（1）$Pearson$相关系数
（2）$Kendall-\tau$（秩相关系数）
2、鞅：
已知过去某一时刻s以及之前所有时刻的观测值，若某一时刻t的观测值的条件期望等于过去某一时刻s的观测值，则称这一随机过程是鞅。
例：若价格随机过程$P(t+1)$满足下述条件，则称为鞅过程：
$E(P(t+1)\mid P(t),P(t-1),......)=P(t)$
3、条件期望
条件期望平滑公式

第二章 估计和检验

数据所在总体的分布类型已知，但其中若干参数未知，要用数据对参数进行统计推断（估计或检验）。

一、点估计

极大似然估计、矩估计
EM算法、MCMC

二、区间估计

正态总体均值的区间估计

三、假设检验

例：次品率、次品率、原假设
把希望的结论放在备择假设上，通过拒绝原假设证明结论。

第三章 大数定律和中心极限定理

一、大数定理

二、中心极限定理

线性插值方法

第四章 数理统计回顾

一、几个基本概念及重要统计量的分布

1、总体、样本、统计量（完全由样本确定的函数）
2、三大统计量分布：卡方分布、t-分布、F-分布
（1）n个互相独立且服从标准正态分布的随机变量平方和服从自由度为n的卡方分布
3、常用分布：
伯努利、二项、泊松、几何分布
正态、指数、均匀分布

第五章 一元线性回归

一、回归函数：线性、多元线性、多项式回归

二、一元线性回归的两种假定

（1）$Gauss-Markov$假定
（2）正态假定

三、回归方程

1、预测在$x_0$，y平均值取值的区间估计（不+e）、y取值区间估计（+e）
2、解释
（1）回归方程有一定的解释范围
（2）截距有时可以解释
（3）斜率的意义

---

第三部分 多元统计

第一章 预备知识

一、主要研究内容

1、多元统计数据的统计推断
参数估计/假设检验

2、简化数据结构（降维问题）
主成分分析/因子分析/对应分析

3、分类和判别
聚类分析/判别分析

4、变量间的相互关系
相互依赖关系：回归分析
变量间的相互关系：典型相关分析
两组变量之间的相互依赖关系：偏最小二乘回归分析

5、多元统计分析的理论基础
统计量->抽样分布理论

二、概率统计基本概念

1、随机变量及其分布/常用分布/数字特征/极限定理
随机变量：随机变量是⼀个取值随机会⽽变化的变量，即⽤定量分析⼯具来研究对应事件及其对应的概率。

2、总体与样本/样本二重性/统计量/参数估计/假设检验
3、随机向量/随机向量的分布及密度函数/边缘密度和条件密度/随机向量的独立性
4、随机向量的期望（均值向量）/期望的线性性质/协方差阵/相关系数阵
5、数据矩阵X（n*p）是p维随机向量$（X1，...，Xp）$的n次实现

6、先验、后验、似然[1]
贝叶斯统计模型：prior、posterior 和 likelihood。posterior=likelihood*prior.

三、数据的图形表示

1、箱形图
最大值、最小值、中位数、上下四分位数
内限：Q1-1.5IQR,Q3+1.5IQR（内限以外：异常值）
外限：Q1-3IQR,Q3+3IQR

2、条形图（分开排列）
简单/分类/堆积条形图

3、直方图（连续排列）

四、多元正态分布

1、性质：二维随机变量边缘分布和条件分布依然是正态分布

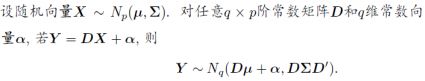
性质3-5：分块矩阵

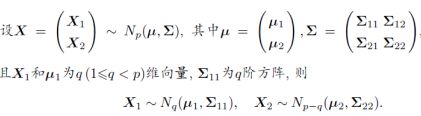
⭐性质6：给定X2时X1的条件分布是q元正态的（二元联合分布均值和方差）

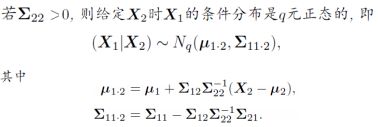
2、常用统计量
（1）样本均值
（2）样本离差阵/样本协方差阵

3、多元正态总体参数的假设检验
（1）均值向量的检验
• t统计量（协方差阵已知/未知）
• F分布
（2）置信椭球
• 类似置信区间

4、正态性检验
（1）图示法
• 直方图+正态密度曲线
• P-P图：变量和理论分布的累积概率
• Q-Q图：变量和理论分布的分位数
• 一致：围绕在一条直线附近
（2）非参数检验
• 基于假设检验问题：服从某特定分布
• K-S检验（大样本）：以样本数的累积频数分布与特定理论分布比较
• S-W检验（小样本）：以顺序统计量为标准

第二章 回归分析

一、预备知识

1、回归方程的检验
相关系数检验/F检验/T检验/残差检验

2、一元线性回归的矩阵形式
未知参数的最小二乘估计

3、多重线性回归模型（经典）
（1）参数估计
（2）问题
• 不再具有直观性
• 变量选择
• 逐步回归法
• 共线性
• 不满秩
• 调整R平方

二、含定性自变量的回归分析

虚拟变量（哑变量）

三、Logistic回归

1、目标：以事件发生的概率p为因变量（单调）
（1）概率与自变量之间关系非线性
（2）p(0,1)
（3）当p接近0，1时，p对自变量的变化不敏感

2、过程：导数f’§非负，且在0和1附近有很大的值
（1）$f^{\prime }(p)=1/p(1-p)$
（2）$f(p)=Inp/(1-p)$
（3）$p=1/1+e^{-z}$

3、公式
$logit(p)=Inp/(1-p)=\beta X$
$p/(1-p)：odds$

4、说明
（1）误差服从0-1分布（伯努利分布）
（2）回归参数估计采用极大似然估计，需要迭代

5、检验
（1）对回归系数的显著性检验：Wald统计量
• 改进方法：增大样本量
（2）对回归方程的显著性拟合优度检验

6、分类：阈值选择
（1）朴素选择：d=0.5
（2）先验选择：d=样本中因变量为1的比例
（3）最优阈值：犯第一类错误最小的原则

第三章 主成分分析

一、思想：方差（信息）

1、几何解释：由原变量$（X_1,X_2,..,X_p)$构成的坐标系旋转得到，代表数据变异最大的方向
正交变换：做旋转（正交阵：AA’=I）

2、代数解释：原来p个变量（单位特征向量）线性组合

二、主成分定义

1、方差大、不相关、个数少

2、ai为单位长度的系数向量：$a_i{a}_i^{\prime }=1$
存在合适的$a_1$使得$Var(Y_1)$最大

3、$a_i$为${\lambda }_i$对应的单位正交特征向量
主成分只与协方差阵有关，与具体分布无关

三、因子载荷

1、每个主成分$Y_i$和变量$X_i$的相关系数
$cov(Y_i,X_j)={\lambda }_i{a}_{ji}$
求$corr(Y_i，X_i)$

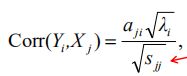
四、从协方差阵出发

1、求法：求出协方差阵的特征值及其对应的单位特征向量
特征值按由大到小排序

2、主成分的基本性质

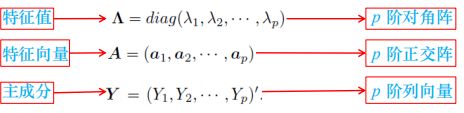
（1）第i个主成分的方差是协方差阵的第i大特征值
（2）总体的总方差等于各主成分的总方差
（3）不同主成分之间是不相关的
（4）总方差等于协方差阵的主对角线元之和

3、贡献率：${\lambda }_i/\Sigma {\lambda }_i$

五、从相关系数阵出发

1、求法：求相关阵R的特征值及其对应的单位特征向量
2、标准化：取值范围不同、量纲不同（不具有可比性）

3、性质
（1）标准后总体的总方差是p
（2）主成分的贡献率：$\lambda i/p$

4、步骤
（1）对数据进行标准化，求相关阵
（2）变量之间的相关性判定
①KMO统计量：用于比较变量间简单相关系数和偏相关系数
• k>0.7效果较好
②Bartlett球形检测：原假设是原变量的相关矩阵是单位阵
• p值接近0，适合主成分分析
（3）计算相关阵的特征值与单位特征向量
（4）确定主成分的个数
（5）主成分的表达式
（6）对主成分进行命名并给予适当解释
辅助其他方法
• 综合评价或排序、聚类分析、判别分析、因子分析
• 主成分回归
• 解决多重共线性问题

第四章 因子分析

• 课程链接：《数据科学》第二章 因子分析

一、主成分分析与因子分析区别

1、主成分分析：把主成分表示成各变量的线性组合；
因子分析：把各变量表示成各因子的线性组合
2、主成分分析：变量变换；
因子分析：构造因子模型，用潜在的假想变量和随机影响变量
3、主成分分析：解释各变量的总方差；
因子分析：重点在于解释各变量之间的协方差
4、主成分分析不需要假设；
因子分析需要假设公共因子存在（公共因子/特殊因子不相关）
5、主成分分析中，Σ或ρ给定，主成分是独特的；因子分析中因子不是独特的，可旋转得不同因子

二、正交因子模型：用潜在变量去解释可观测原始变量

1、X：可观测的p维随机向量，均值向量u，协方差阵
2、F：不可观测的m维随机向量（公共因子）
3、ε：与F不相关，协方差阵是对角阵D（特殊因子）
4、因子载荷矩阵A：变量与公共因子之间的相关系数

三、性质

1、正交因子模型的协方差结构
（1）随机向量X的协方差阵Σ
（2）随机向量X与公共因子F的协方差阵A

2、变量X方差=共性方差（A每行的平方和）+剩余方差

3、贡献：A每列的平方和，表示第j个公共因子$F_j$对X所有分量的总影响

4、公共因子的不唯一性

四、主要步骤

1、估计因子载荷：提取公共因子
（1）因载荷矩阵的估计：主成分法
• 从样本相关阵R出发，特征值为λ（p个）
• 谱分解（p个）
• 只取前面的m个
• 得到：A和D，即主成分解（估计）
（2）公共因子数的确定：m

2、进行因子旋转：正交旋转
（1）目的：“简单结构原则”，不利于解释
（2）原理：将因子载荷矩阵右乘一正交矩阵，不改变因子模型的协方差结构，所以不改变协方差阵或相关阵的估计，不改变共性方差和特殊方差的估计
• 线性代数：正交变换对应坐标轴的旋转
• 正交阵的性质
• 矩阵本身可以看成向量的向量
• 性质1：保证向量长度不变
• 性质2：保证向量夹角不变
（3）应用
• 奇异值分解
• 谱分解
（4）步骤
• 初始因子载荷矩阵A，二阶正交矩阵Г（含角度）
• 角度确定：尽量分散（迭代，收敛到最优解）
• 因子旋转的方法：最大方差法
• 无论怎么旋转，共性方差保持不变
• 考虑每组数的相对方差，求一个合适的m阶正交阵Γ使得总相对方差V达到最大

3、计算因子得分（对不可观测随机向量F的取值估计）
（1）回归法
（2）加权最小二乘法

---

第四部分 时间序列分析

• 课程关联：《金融风险管理》第四章 金融时间序列

第一章 时间序列分析简介

一、时间序列定义

1、随机序列{$X_t$}：按时间顺序排列的一组随机变量
2、观察值序列$（x_1,...,x_n）$：随机序列中n个有序观察值

二、时间序列分析方法——描述性、统计

1、描述性时序分析
2、统计时序分析
（1）频域分析方法（谱分析）
• 原理：分解成若干不同频率的周期波动
• Fourier分析
• 最大熵谱估计
（2）时域分析方法
• 原理：惯性-相关关系-统计规律
3、分析步骤：观察数据特征、选择合适模型、确定模型口径、检验优化模型、推断预测

三、时间序列特征及分析方法——确定性/随机性分析

1、长期趋势
2、季节变动
3、循环波动：非固定周期的反复循环波动
4、随机波动：噪声，平稳序列
1、2、3=>非平稳时间序列=>分析方法：随机性分析、确定性分析

确定性分析
定义：某一确定性因素对序列的影响，推断各种确定因素之间的相互作用关系和对序列的综合影响
• 典型分解式法：$X_t=m_t$（趋势项）$+s_t$（季节项）$+Y_t$（平稳随机噪声项）
• 差分法：对数据反复作用差分因子，直至平稳
• 趋势分析
①趋势拟合法：把时间作为自变量。易受到异常点的影响，自动忽略短期变化（季节性变化），对仅有趋势和随机波动的时间序列表现才比较好
②平滑法（滑动平均法、指数平滑法）：修匀技术，削弱短期随机波动，显示出长期趋势变化。

随机性分析
• 随机时间序列模型：仅用过去值和随机扰动项建立模型
• 发展过程：基础-核心-完善
①基础阶段
AR模型：自回归
MA模型：滑动平均
ARMA模型

②核心阶段
ARIMA模型：又称Box-Jenkins模型，求和自回归滑动/自回归差分滑动
• 单变量，同方差场合的线性模型

③完善阶段
异方差
• ARCH模型/GARCH模型
多方差
• 协整理论
非线性

四、时间序列的预处理——平稳性和纯随机性

基本描述：有限维分布函数：时间序列{Xt}的概率分布
均值函数：$\mu$
方差函数：${\sigma }^2$
自协方差函数：$\gamma （t,s）$
自相关函数：$\rho （t,s）$

1、平稳性检验（处理方法：差分、Box-Cox变换）
（1）图方法
• 时序图
①常数值附近随机波动
②波动范围有界、无明显趋势及周期特征
• 自相关图：平稳序列通常具有短期相关性，平稳序列的自相关系数会逐渐衰减到0

（2）单位根检验
• ADF检验：主要适用于方差齐性场合
• PP检验：适用于异方差场合 的平稳性检验

2、纯随机性检验
纯随机性：$\gamma （k）=0$（纯随机性是相关信息是否提取充分的一个判断标准）
• 白噪声序列
• 方差齐性：$Var（X_t）=\gamma （0）$
方法：
①原假设H0为具有纯随机性，检验统计量：Q统计量、LB统计量（修正后的Q统计量）
②游程检验
• 检验单样本变量值是否随机
• 原理：中心极限定理

3、异常值处理
插补
平均值修正

4、缺失值处理
插补

第二章 预备知识

一、差分运算

1、p阶差分：消除趋势影响
${\Delta }^p{x}_t={\Delta }^{p-1}{x}_t-{\Delta }^{p-1}{x}_{t-1}$
2、k步差分：消除周期性影响
$x_t-x_{t-k}$

二、延迟算子

1、差分与延迟算子
$\Delta =1-B$
$B=X_{t-1}/X_t$

2、线性趋势用一阶差分，抛物线用二阶差分，周期为s的季节差分
$Y_t=（1-B）X_t=X_t-X_{t-1}$
$Y_t=（1-B{）}^2\ast X_t=X_t-2X_{t-1}+X_{t-2}$

三、线性差分方程

1、Samuelson经典模型

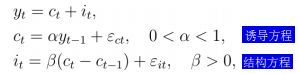
诱导方程：将当期变量值表示成该变量滞后值，其它内生变量滞后值，外生变量的当期值和过去值以及扰动项的函数。
结构方程：表明了两个当期内生变量$c_t$和$i_t$之间满足某个约束条件或系统结构。

2、齐次线性差分方程的解
（1）目标方程、特征方程

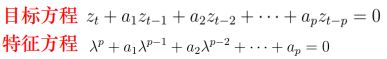
• 一元p次方程，p个非零根：特征根λ
（2）不同场合下的通解
• 不相等实数根场合
• 有相等实数根场合
• 复根场合

3、非齐次线性差分方程的解
通解+特解

4、⭐求特殊解的一些例子
• 常数
• 线性特解
• 二阶、三阶、…、p阶

一阶差分方程

延迟算子：泰勒展开“1-aB”可以看作“1-x”

四、判断平稳/非平稳

1、主要思想
（1）决定过程特性的统计规律不随时间而改变
（2）分类
严平稳
• 随机向量平移任意时间后保持分布不变
• 和时间起点无关
宽平稳
• 二阶矩存在
• 均值函数为常数
• 协方差函数只与时间差有关$\gamma （r,s）=\gamma （r+t,s+t）$

2、平稳时间序列的统计性质
（1）常数均值
（2）自协方差函数和自相关函数只依赖于时间的平移长度而与时间的起止点无关
延迟k自协方差函数：$\gamma （k）=\gamma （t，t+k）$
延迟k自相关系数：$\rho （k）=\gamma （k）/\gamma （0）$

（3）自相关系数主要性质
规范性
对称性：$\rho （k）=\rho （-k）$
非负定
非唯一性：自相关系数不能决定序列

3、简单例子（判断）
（1）白噪声序列（平稳）：无序列相关性
由一列两两不相关的随机变量，且均值方差为常数
建模没有意义，因为不相关，得到期望、方差即可
（2）随机游走（非平稳）
设{Xt}是一列均值为0，方差为常数的独立同分布的随机变量序列，$Y_t=Y_{t-1}+X_t$，称Yt为随机游走序列
（3）滑动平均（平稳）
设$X_t$同上，$Y_t=（X_{t-1}+X_t）/2$
均值为0，协方差只依赖时间长度

4、平稳时间序列的参数估计
均值、协方差函数、方差、自相关系数（同一般意义上）

第三章 ARMA模型

一、AR（p）模型

1、中心化

2、AR（p）平稳性判断
（1）特征根判别（一般情形）：特征根和自回归系数多项式的根成倒数的性质
• 充要条件：p个特征根都在单位圆内
• 自回归系数多项式的根都在单位圆外
（2）平稳域判别（低阶情形）
• 参数向量Φ只能为p维欧式空间的一个子集
低阶AR模型的平稳域

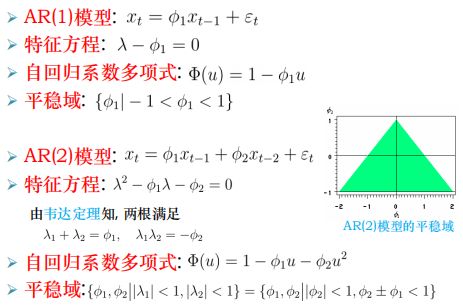
3、⭐Green函数
中心化AR（p）模型：$\Phi （B）x_t={\epsilon }_t$
传递形式：$\Phi （B）G（B）{\epsilon }_t={\epsilon }_t$（待定系数法）

4、平稳AR模型的统计性质
（1）均值u:中心化
（2）方差

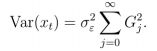
• 无须考虑交叉项
• 方差函数有界且为常数

（3）自协方差函数
• 递推公式

（4）自相关函数：拖尾性、指数衰减
• 递推公式

• AR（1）、AR（2）

（5）偏自相关系数
• 定义：在给定中间k-1个随机变量$x_{t-1},x_{t-2},...,x_{t-k+1}$的条件下，剔除中间k-1个随机变量的干扰之后，$x_{t-k}$对$x_t$影响的相关程度。
• AR(1)、AR(2)、p阶截尾

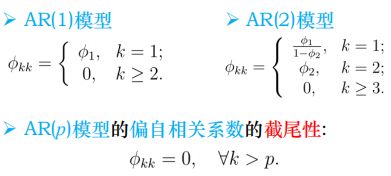
• 公式（Yule-Walker方程）：Cramer法则[1]，求${ф}_{kk}$

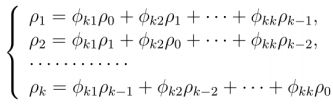
二、MA（q）模型

1、移动平均系数多项式：$\Theta （B）$

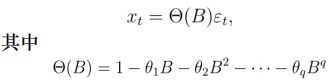
2、统计性质

（1）常数均值
（2）常数方差
（3）自相关函数：q阶截尾（自协方差函数：q阶截尾）
（4）偏自相关系数：拖尾性
例：MA(1)、MA(2)自相关函数

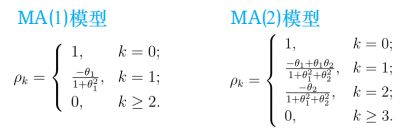
MA(1)偏自相关系数

3、可逆性（自相关系数对应模型不唯一，因此引入可逆性条件确保唯一性）
一个MA模型能表示成收敛的AR模型形式，称为可逆模型。

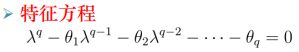
（1）充要条件：特征根都在单位圆内，等价于移动平均系数多项式的根都在单位圆外
（2）MA模型的可逆性和AR模型的平稳性是完全对偶的

4、逆转函数{I…}

三、ARMA（p，q）模型

1、中心化平稳可逆的ARMA模型
平稳性和可逆性
传递形式和逆转形式

2、统计性质
均值
自协方差函数
自相关系数：拖尾性

偏自相关系数：拖尾性

3、平稳时间序列的建模

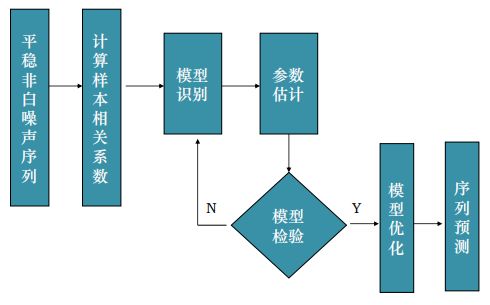
（1）平稳非白噪声序列
（2）计算样本相关系数
（3）模式识别
• 理论
• 根据自相关系数和偏自相关的拖尾性或截尾性
AR：拖尾+截尾，MA：截尾+拖尾，ARMA：拖尾+拖尾

• 经验定阶方法
• n→∞，样本自相关系数和偏自相关系数渐进正态性
• 从而，利用2倍标准差范围来辅助判断

（4）参数估计（p+q+2个参数）

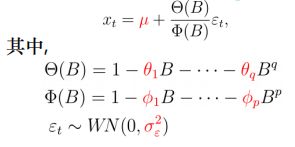
• 矩估计（均值）
• 极大似然估计
• 最小二乘估计

（5）模型检验
• 模型的显著性检验：残差序列为白噪声序列，说明信息提取充分
• 参数的显著性检验：显著非零（t统计量）

（6）模型优化
①AIC准则（最小信息量准则）
指导思想：对拟合精度和未知参数个数进行平衡，使AIC函数达到最小的模型被认为是最优的

不足：样本容量n很大时表现比较差=>改进：BIC准则（贝叶斯）
②SC准则
• 改进：将未知参数个数的惩罚权重由常数2变成In n

（7）序列预测——线性最小方差预测
①依据：$x_t$是历史数据$x_{t-1}、x_{t-2}...$的线性函数

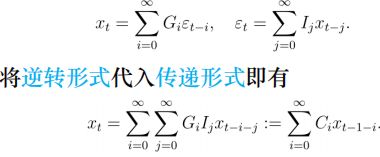
• 线性预测和误差
• 第l步预测
• 预测误差

②预测原则：预测方差最小原则
• 预测方差只与预测步长l有关（条件无偏最小方差估计）

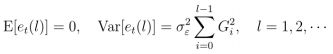
• 置信区间

③动态预测与静态预测
动态预测
• 根据估计区间，进行多步向前预测，每一步都是采用前面的预测值来计算新的预测值，只适用于样本外预测
• 总结：样本外的多部预测

静态预测
• 滚动的进行向前一步预测，即每预测一次用真实值代替预测值，加入到估计区间，再进行向前一步预测，只适用于样本内或向前一步样本外预测。
• 总结：样本内模型的拟合值（估计值）或向前一步预测

第四章 非平稳时间序列

一、ARIMA（p，d，q）：差分和ARIMA

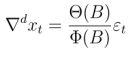
2、判断为ARMA还是ARIMA模型：是否能写成$（1-B）x_t$的形式

二、非平稳时间序列建模步骤

（d阶）单整序列：（d次）差分
1、差分提取线性/曲线趋势
2、差分提取固定周期信息
3、过差分：α信息（一阶差分）、β信息（二阶差分）

三、其他模型——疏系数模型、简单季节模型

1、疏系数模型：系数一部分为0
2、简单季节模型
（1）加法季节模型
时间序列中的季节效应和其他效应之间是加法关系
（2）乘积季节模型（更常见）
时间序列的季节效应、长期趋势和随机效应之间存在复杂的交互影响关系

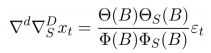
例题

1、AR模型
• 预测值、利用Green函数计算预测方差

2、MA模型（只能预测q步之内的序列）
• 未来预测值和计算预测方差

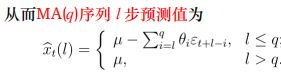
3、ARMA预测

4、ARIMA模型
预测：
（1）原则：最小均方误差
（2）方法：递推
（3）广义自相关函数