python pca主成分分析

主成分分析算法（PCA）是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留住较多的原数据点的特性。

具体原理：PCA：详细解释主成分分析_lanyuelvyun的博客-CSDN博客_pca 

Python机器学习笔记：主成分分析（PCA）算法 - 战争热诚 - 博客园 (cnblogs.com)

import numpy as np
import cv2

def pca(X):
    """
主成分分析的步骤：
1 去除平均值
2 计算协方差矩阵
3 计算协方差矩阵的特征值和特征向量
4 将特征值排序
5 计算方差贡献率
    输入：矩阵X，存储训练数据，每一行为一条数据
    """
    # 获取维数
    num_data ,dim = X.shape
    # print(num_data,dim)
    # 数据中心化（减去每一维的均值）
    """
    这里每一行代表的是一个样本，列数代表的是样本的特征。pca的目标是减少列数
    # hh=X[:,0]
    # a=np.mean(hh)
    # print(a)
    """
    #求样本的均值
    mean_X = X.mean(axis = 0)
    #去中心化
    X = X -mean_X
    #协方差矩阵
    # M1 = np.dot(X.T, X)
    M = np.cov(X, rowvar=0)
    # 特征值和特征向量
    W,V = np.linalg.eig(np.mat(M))
    a=np.argsort(-W)  ##返回的是元素值从小到大排序后的索引值的数组
    #计算主成分贡献率和累计贡献率
    sum_lambda=np.sum(W)  #特征值的和
    for i in range(len(a)):
        f=np.divide(W[a[:i]],sum_lambda)#计算每个特征值的贡献率
        sum=f.sum()
        if sum>0.97:
            count=i
            break
    # print(a[:count])
    print('原来的维数',len(a))
    print('降维后的维数',count)
    V1=V[:,a[:count]]
    #降维后的数据
    Y=X*V1
    ##
    y=Y*V1.T+mean_X
    return Y,y

img=cv2.imread('img1.png',0)
# img=cv2.resize(img,(5,6))
img1,img2=pca(img)

def pca(X, topNfeat = 3):
    mean_X = np.mean(X, axis=0) # 竖着求平均值，数据格式是m×n
    mean_removed = X - mean_X  # 0均值化  m×n维
    M = np.cov(mean_removed, rowvar=0)  # 每一列作为一个独立变量求协方差  n×n维
    W, V = np.linalg.eig(np.mat(M)) # 求特征值和特征向量  eigVects是n×n维
    eigValInd = np.argsort(-W)  # 特征值由大到小排序，eigValInd十个arrary数组 1×n维
    eigValInd = eigValInd[:topNfeat]  # 选取前topNfeat个特征值的序号  1×r维
    redEigVects = V[:, eigValInd] # 把符合条件的几列特征筛选出来组成P  n×r维
    lowDDataMat = mean_removed * redEigVects  # 矩阵点乘筛选的特征向量矩阵  m×r维 公式Y=X*P
    reconMat = (lowDDataMat * redEigVects.T) + mean_X  # 转换新空间的数据  m×n维
    return lowDDataMat, reconMat

总的代码

import numpy as np
import cv2
from sklearn.decomposition import PCA
def pca(X):
    """
主成分分析的步骤：
1 去除平均值
2 计算协方差矩阵
3 计算协方差矩阵的特征值和特征向量
4 将特征值排序
5 计算方差贡献率
    输入：矩阵X，存储训练数据，每一行为一条数据
    """
    # 获取维数
    num_data ,dim = X.shape
    # print(num_data,dim)
    # 数据中心化（减去每一维的均值）
    """
    这里每一行代表的是一个样本，列数代表的是样本的特征。pca的目标是减少列数
    # hh=X[:,0]
    # a=np.mean(hh)
    # print(a)
    """
    #求样本的均值
    mean_X = X.mean(axis = 0)
    #去中心化
    X = X -mean_X
    #协方差矩阵
    # M1 = np.dot(X.T, X)
    M = np.cov(X, rowvar=0)
    # 特征值和特征向量
    W,V = np.linalg.eig(np.mat(M))
    a=np.argsort(-W)  ##返回的是元素值从小到大排序后的索引值的数组
    #计算主成分贡献率和累计贡献率
    sum_lambda=np.sum(W)  #特征值的和
    for i in range(len(a)):
        f=np.divide(W[a[:i]],sum_lambda)#计算每个特征值的贡献率
        sum=f.sum()
        if sum>0.97:
            count=i
            break
    # print(a[:count])
    print('原来的维数',len(a))
    print('降维后的维数',count)
    V1=V[:,a[:count]]
    #降维后的数据
    Y=X*V1
    ##
    y=Y*V1.T+mean_X
    return Y,y

def pca1(X, topNfeat = 5):
    mean_X = np.mean(X, axis=0) # 竖着求平均值，数据格式是m×n
    mean_removed = X - mean_X  # 0均值化  m×n维
    M = np.cov(mean_removed, rowvar=0)  # 每一列作为一个独立变量求协方差  n×n维
    W, V = np.linalg.eig(np.mat(M)) # 求特征值和特征向量  eigVects是n×n维
    eigValInd = np.argsort(-W)  # 特征值由大到小排序，eigValInd十个arrary数组 1×n维
    eigValInd = eigValInd[:topNfeat]  # 选取前topNfeat个特征值的序号  1×r维
    redEigVects = V[:, eigValInd] # 把符合条件的几列特征筛选出来组成P  n×r维
    lowDDataMat = mean_removed * redEigVects  # 矩阵点乘筛选的特征向量矩阵  m×r维 公式Y=X*P
    reconMat = (lowDDataMat * redEigVects.T) + mean_X  # 转换新空间的数据  m×n维
    return lowDDataMat, reconMat

img=cv2.imread('img1.png',0)
img=cv2.resize(img,(8,8))
img1,img2=pca(img)
img3,img4=pca1(img)

pca=PCA(n_components=5)
pca.fit(img)
img5=pca.transform(img)
##打印各个主成分的方差值占总方差值的比例，即方差贡献率
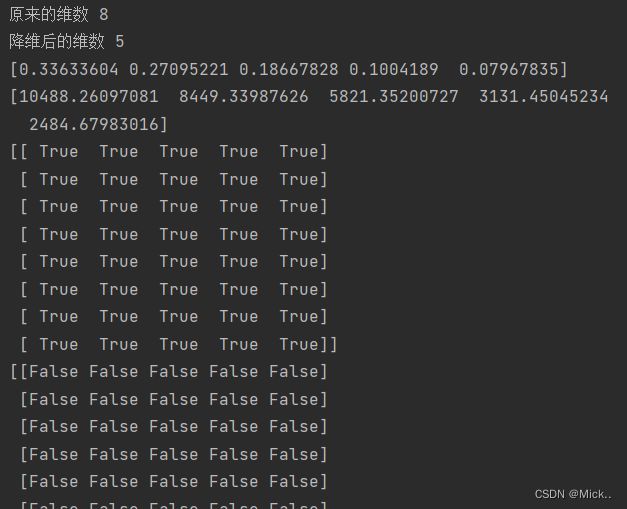
print(pca.explained_variance_ratio_)
#打印降维后的各个主成分的方差值
print(pca.explained_variance_)
print(img1==img3)
print(img1==img5)
print(img2==img4)

 

参考文献

PCA：详细解释主成分分析_lanyuelvyun的博客-CSDN博客_pca

计算机视觉：基于Numpy的图像处理技术（二）：图像主成分分析（PCA）_天海一直在的博客-CSDN博客

机器学习实战之PCA - 卑微的蜗牛 - 博客园 (cnblogs.com) 

如何理解“方差越大信息量就越多”？ - 知乎 (zhihu.com)