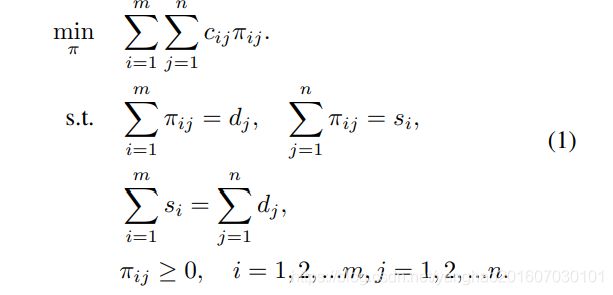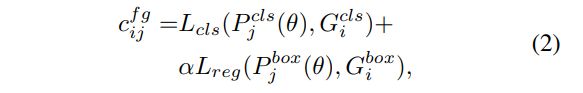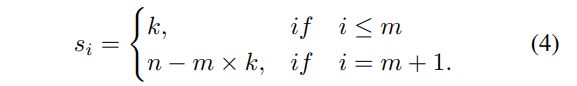论文阅读|目标检测之基于OTA，以最佳传输优化来实现新的基于CNN的一对多标签分配策略

• Paper: https://arxiv.org/abs/2103.14259
• Code: https://github.com/Megvii-BaseDetection/OTA（基于cvpods）

论文提出了一种基于最优传输理论的目标检测样本匹配策略，利用全局信息来寻找最优一对多样本匹配的结果，相对于现有的样本匹配技术，具有如下优势：1). 检测精度高。全局最优的匹配结果能帮助检测器以稳定高效的方式训练，最终在COCO数据集上达到最优检测性能。2). 适用场景广。现有的目标检测算法在遇到诸如目标密集或被严重遮挡等复杂场景时，需要重新设计策略或者调整参数，而最优传输模型在全局建模的过程中包括了寻找最优解的过程，不用做任何额外的调整，在各种目标密集、遮挡严重的场景下也能达到最先进的性能，具有很大的应用潜力。

摘要

当前的标签分配都旨在给每个gt独立地定义正负训练样本，而本文从全局角度出发来制定标签分配策略，提出将标签分配策略看作一种传输优化问题，该问题以再优化领域比较成熟。具体而言，我们将每对需求者（anchor）和提供者（gt）之间的单元传输代价定义为他们的分类和回归的损失之和。这样构建之后求最好的分配策略就转变成解最佳传输方案以得到一个最小的传输代价，而这可以通过Sinkhorn-Knopp迭代得到。

On COCO, a single FCOS-ResNet-50 detector equipped with Optimal Transport Assignment (OTA) can
reach 40.7% mAP under 1× scheduler, outperforming all other existing assigning methods.

1. Introduction

要训练检测器，为每个锚点定义cls和reg目标是必要的过程，在对象检测中称为标签分配。经典标签分配策略通常采用预定义规则来给每个anchor匹配gt对象或背景。

RetinaNet使用IoU阈值作为anchor的正负标签分配标准。

anchor free的FCOS把任何处于gt的边框内部（或者中心区域内）的点（实际上也可以看作这里样本是anchor points）视作正样本，但是这忽略了不同尺寸、形状和遮挡请跨下的物体其正负划分标准不同。

于是受此启发，出现一批动态的标签分配策略。

如ATSS根据统计特征来设计每个gt的划分标准，PAA等提出每个anchor预测的置信度得分可以作为标签分配的一个适当指标，高置信度的anchor容易通过网络学习，所以被分为正样本，而哪些低置信度的anchor应该被视为负样本。这种策略使得网络能够动态地为每个gt选择正样本anchor，从而实现SOTA表现。

然而，独立地为每个gt分配正负样本而不考虑上下文背景（context）得到的结果是次优的，当处理模糊样本anchors（同时被分配为多个gt的正样本的anchor，如图1所示）时，现存的分配策略都依赖于认为设定的分配规则（如FCOS将其分配给最小面积的gt，而其他想RetinaNet这样基于IOU则是将之分配给IoU最大的gt），作者认为将模糊的anchor分配给任何gt或背景都会对其他gt的梯度造成不利影响，因此，对模糊anchor样本的分配是特殊的，除了局部视图之外还需要其他信息。因此，更好的分配策略应该摆脱对每个gt对象进行最优分配的惯例，而转向全局最优的思想，换句话说，为图像中的所有gt对象找到全局的高置信度分配。

DeTR 是第一个尝试从全局角度考虑标签分配的工作。 它用transformer层替换了检测头，并使用匈牙利算法一对一分配，该算法仅对每个gt匹配一个具有全局最小损耗的query 。 但是，对于基于CNN的检测器，由于网络通常会产生与目标周围相邻区域相关的分数，因此每个gt会分配给许多anchors（即一对多），这也有利于训练效率。 以一对多的方式，分配具有全局视图的标签仍然完好无损。

为了在一对多的情况下实现全局最优分配结果，我们建议将标签赋值公式化为最优运输（OT）问题-优化理论中的线性规划（LP）的一种特殊形式。 提供一定数量的标签，并将每个锚定义为需要一个单位标签的需求。 如果锚从某个gt接收到足够数量的阳性标记，则此锚将成为该gt的一个阳性锚。 在这种情况下，每只吉卜赛阳性标记的数量可以解释为“在训练过程中需要多少阳性锚以更好地收敛”。 每个锚定对之间的单位运输成本被定义为它们的成对的clsandregloss的加权总和。 此外，由于每个锚点也应考虑为负号，因此我们引入了另一家供应商-Background，该供应商将提供负号标签以构成需要的其余标签。 背景和特定锚之间的成本仅定义为它们的成对分类损失。 制定公式后，将找到最佳分配解决方案的问题转换为最佳运输计划，可以通过现成的Sinkhorn-Knopp迭代快速有效地解决该问题[5]。 我们将这种分配策略命名为“最佳运输分配（OTA）”

实验表面，OTA带来了显著的进步。

2. Related work

2.1 Fixed Label Assignment

基于anchor的检测器中以固定的IoU阈值作为标签分配的标准的。

anchor-free中像FCOS这样只根据是否样本落入某个gt内部的。

2.2 Dynamic Label Assignment

GuidedAnchoring

MetaAnchor

NoisyAnchors

FreeAnchor

ATSS

PAA

AutoAssign

以上这些方法都是为单个物体寻找最佳分配策略，缺少从全局角度出发考虑上下文信息。DeTR展示了全局最佳匹配的思想，但是它所采用的匈牙利算法只适用于一对一的匹配方式。目前基于CNN的一对多标签分配中还缺少一个全局的最佳分配策略。

3. Method

3.1 Optimal Transport

最佳运输（OT）描述了以下问题：假设在某个领域中存在m个suppliers（供应者）和n 个demanders（需求者）。 第i个供应商持有$s_i$个单位商品，第j个需求者需要$d_j$个单位商品。 供应商i到需求者j之间每单位商品运输成本用$c_{ij}$表示。而OT的目的是找到一个最佳的传输计划${\pi }^{\ast }=\left\{{\pi }_{i,j}|i=1,2,...m,j=1,2,...n\right\}$，据此，可以以最小的运输成本将来自供应商的所有商品运输到需求者。

这是一个线性程序，可以在多项式时间内求解。 但是，在我们的情况下，所得的线性程序很大，涉及特征维度的平方与所有尺度的anchor。 因此，我们通过一个名为Sinkhorn-Knopp的快速迭代解决方案来解决此问题。

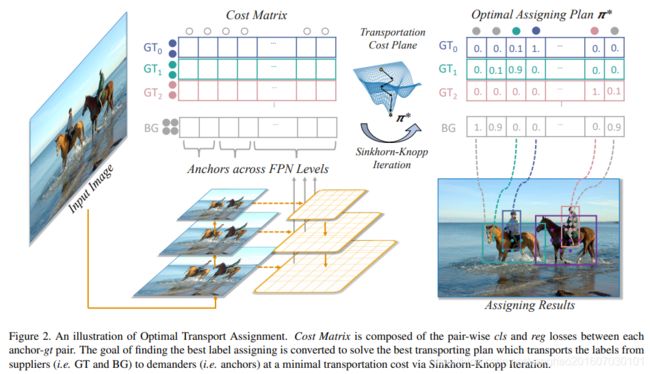
3.2. OT for Label Assignment

在目标检测的背景下，假设一张输入图片中有m个gt targets和n个anchors（所有FPN层的），我们将每个gt视作有k个单元的正标签（positive label）的suppliers(i.e., $s_i=k,i=1,2,...,m$)，每个anchor视作需要一个单元标签的demander (i.e.,
$d_j=1,j=1,2,...,n$)，将一个单元的标签从$g{t}_i$传到anchor $a_j$的代价$c^{fg}$定义为它们cls和reg losses的加权相加：

其中$P_j^{cls},P_j^{box}$分别指$a_j$预测的分类得分和边框$G_i^{cls},G_i^{box}$指代的是gt i的类别和bbox，$L_{reg},L_{cls}$指的是IoU loss和entropy loss，当然也可以使用GIOU loss和Focal Loss来替换。$\alpha$是一个平衡系数。

除了正标签，训练时大量的anchors还会被分配为负标签，成为负样本。由于最佳传输涉及所有的anchors，所以引入另一个supplier——background，它只提供负标签，并且提供的总数为n - m×k，从而使得总的supply等于总的demand。将一个单元的负标签从background传输到anchor $a_j$的代价为：
$$c_j^{bg}=L_{cls}(P_j^{cls}(\theta ),\varnothing ),(3)$$

其中∅表示background类。将这个$c^{bg} \in \mathbb{R}^{1×n} $concatenate到$c^{fg} \in \mathbb{R}^{m×n} $后得到代价矩阵$c \in \mathbb{R}^{(m+1)×n} $，这样提供者s一个相应地更新为：

得到带家具在c，提供者s以及需求者d后，就可以通过现成的Sinkhorn-Knopp迭代法解决该OT问题，从而获得最优的运输计划${\pi }^{\ast }\in {\mathbb{R}}^{（m+1）\times n}$。得到${\pi }^{\ast }$后，可以通过将每个anchor分配给向其传输最多标签的提供者supplier来解码对应的标签分配解决方案。后续过程（例如，基于分配结果计算损失，反向传播）是完全相同的 如FCOS 和ATSS [。 请注意，OT问题的优化过程仅包含一些矩阵乘法，可以由GPU设备加速，因此OTA仅将总训练时间增加了不到20％，并且在测试阶段完全cost-free。

3.3. Advanced Designs

Center Prior. 先前的工作仅从对象的有限区域的中心区域中选择正anchor，称这个中心区域为（Center Prior）先验中心。这是因为他们的分配策略中存在大量模糊样本或者接下来的处理中缺少统计数据。我们的OTA无需依赖统计特征，而是基于全局优化方法，因此自然可以抵御这两个问题。 从理论上讲，OTA可以将gt框内的任何一个anchor分配为正样本。但是，对于像COCO这样的常规检测数据集，我们发现Center Prior 有利于OTA的训练。 强迫检测器将注意力集中在潜在的积极领域（即中心区域）可以帮助稳定训练过程，尤其是在训练的早期阶段，这将导致更好的最终表现。 因此，我们在代价矩阵上加了一个Center Prior。 对于每一个gt，我们根据anchors和gt之间的中心距离从每个FPN级别中选择$r^2$个最接近的anchors。 对于不在前$r^2$中的anchor，它们在代价矩阵c中的对应匹配entries将受到附加的常量代价，以减少在训练阶段将它们分配为正样本的可能性。 参见第4节，我们将证明，尽管OTA像其他方法一样采用了一定程度的“Center Prior”，但通过设置一个很大的r（使得包括大量潜在的正anchors和更多模糊anchors），OTA比其他方法表现更好。

Dynamic k Estimation. 直观来看，每个gt的适合的anchos数量（见3.1节）应该有所不同，并应基于许多因素，例如对象的大小，比例和遮挡条件等。因为难以直接建立一个可以根据这些因素得到相应正anchors数量的函数，我们提出了一种简单但有效的方法，即根据预测的边界框和gt之间的IoU值，粗略估计每个gt的正anchor的适当数量。 具体来说，对于每个gt，我们根据IoU值选择top q预测。这些IoU值相加，以代表此gt的估计正锚数。 我们将此方法命名为Dynamick Estimation。 这样的估计方法基于以下直觉：某个gt适合的正anchor数量应与充分回归该gt的anchor的数量正相关。 在第4节中，我们将对fixed k和Dynamic k Estimation策略进行详细的比较。OTA的可视化如图2所示。我们还在算法1中描述了OTA的完整过程，包括CenterPrior和Dynamic k Estimation。

4 . Experiments

OTA能同时在anchor-based和anchor-free的检测器上展开，文章为了简便，主要的实验是基于FCOS来实现的。

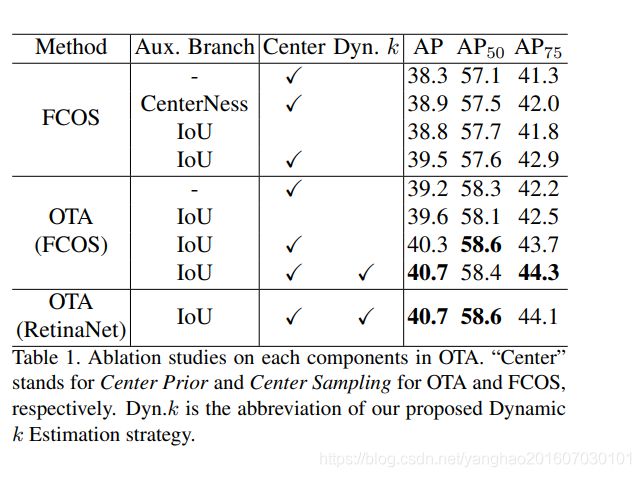
PAA中证明了IoU Branch的作用，因此这里还加入了这个分支，此外实验中还有Center Prior分支作为消融实验。此外，为了展示了每个独立部分的作用，消融实验这展示了Center Prior中r的效果，以及OTA对模糊样本的处理，OTA相比原来人为设定的模糊样本处理方式表现更佳，尤其是在处理遮挡上， OTA表现很好，实验中还讨论了每个supplier（gt+bg）能提供的标签数量，即k，分为采用固定数量和动态数量，即dynamic k，后者更优。这些实验的数据如下：

几种分配策略的可视化如下：

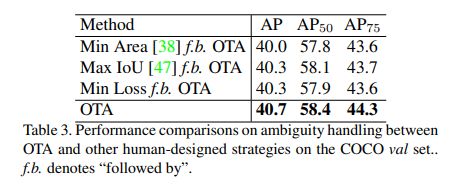
模糊处理的几种方式比较：

不同的k值比较：

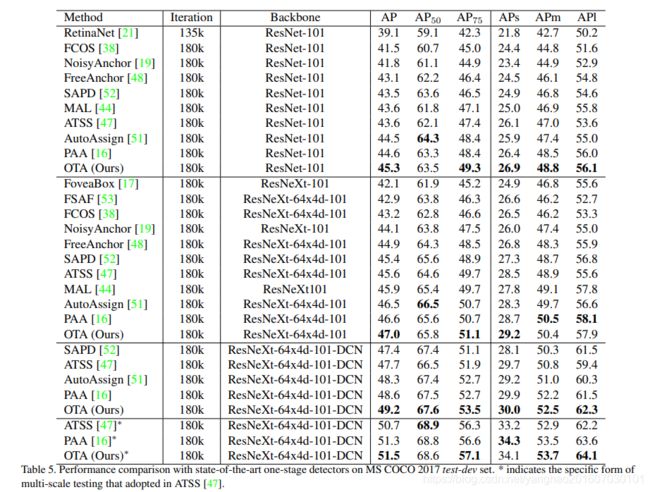
和SOTA检测器的比较：

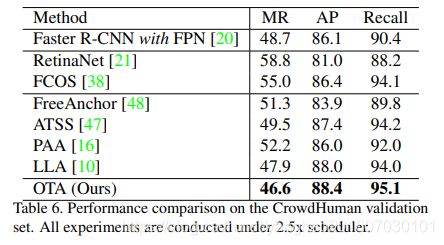
为了显示器处理遮挡的能力，单独在CrowdHuman数据集上做了测试：

5. Conclusion

文章提出一种新的标签分配策略——Optimal Transport Assignment (OTA)，该策略将gt和bg的标签分配给anchor的过程转变成一个最优化的问题，使用SinkhornIter迭代求解得到最小的分配代价矩阵c，解码该分配代价矩阵c后得到最佳分配方案，然后剩余工作（求总loss，反向传播等）即可和FCOS等一样进行。为了决定每个gt的能够分配的标签数量，进一步设计了一个能够基于预测的边框和gt的IoU值来估计的策略，即dynamic k estimation。实验表明，OTA在MS COCO上达到了SOTA。因为OTA可以很好地处理模糊anchor的分配，所以它在CrowdHuman数据集上的优势也很大，胜过CrowdHuman数据集上的所有其他阶段的检测器，证明了其强大的泛化能力。