《Diffusion Models Beat GANs on Image Synthesis》阅读笔记

《Diffusion Models Beat GANs on Image Synthesis》阅读笔记

1 Motivation

（1）GAN模型可以获得很高的生成质量，但是高质量是通过牺牲多样性实现的，并且GAN模型的设计需要精密的参数选择，否则很容易崩溃，这些缺点限制了GAN模型在下游任务的应用。

（2）目前对GAN模型架构上的研究非常丰富，有比较完善的实验探究结果。

（3）扩散模型已经被证明可以生成高质量的图像，并且相比于GAN能够更好地覆盖样本分布，但对扩散模型架构的研究相对较少，扩散模型仍有继续改进的潜力。

2 Contribution

（1）从GAN的实验中得到启发，对扩散模型进行大量的消融实验，找到了更好的架构。

（2）在ImageNet的生成任务中打败了最先进的BigGAN，在128×128的图像上FID达到2.97；在256×256的图像上FID达到4.59，在512×512的图像上FID达到7.72。同时，扩散模型比BigGAN更好地匹配了数据分布。

3 扩散模型介绍

扩散模型的思想是，对于数据分布$x_0\backsim q(x_0)$，前向构造$t=1,2,...T$共$T$个不同时段（代表不同噪声等级）的先验加噪（高斯噪声）概率分布$x_t\backsim q(x_t|x_0)$。之后，从$x_T$开始，逐步反向预测前一个时刻的分布$x_{t-1}\backsim p(x_{t-1}|x_t)$，直到回溯到$x_0$，使得预测的分布$p(x_0)$与真实分布$q(x_0)$相近。整个时序具有马尔科夫链的性质。

3.1 前向分布构造

对于每一个时间步$t$，根据马尔可夫噪声过程，其分布可以表示为如下形式：

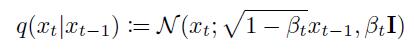
上述公式的含义可以理解为，$t$步图像由$t-1$步的数据添加球面高斯噪声得到，${\beta }_t$是$t$步添加的噪声方差信息，预先给定，通常为一个常数。

如果使用上面的公式进行$x_t$的先验概率分布计算，那么一共需要进行$T$次采样，根据高斯分布的性质，可以直接采样$q(x_t|x_0)$，得到每一个时步关于$x_0$的先验条件概率分布：

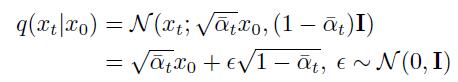
这里的$ϵ$表示引入的球面高斯噪声。上式中的每个${\bar{\alpha }}_t$包含了其前面所有时步的方差信息：

结合上面的两个公式，就可以得到$x_{t-1}$关于$x_t$和$x_0$的联合后验分布，这个分布显然也是个高斯分布：

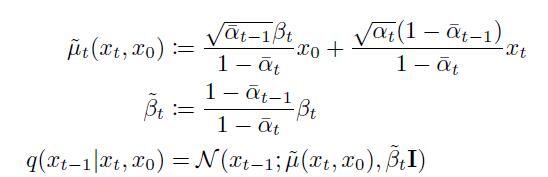
综合上面的公式，假如想要采样一个$x_0$，那么可以先通过饱含噪声的$x_T$，一步步进行逆推，直到回溯至$x_0$，因此，如果我们可以构建出一一系列与$q(x_{t-1}|x_t)$相吻合的分布，那么就可以通过反向马尔可夫过程，将随机噪声反推到图像分布上。所以，扩散模型的任务就是找到与$q(x_{t-1}|x_t,x_0)$相似的分布。

3.2 反向分布构造

根据前向分布的构造过程，可以假定反向分布$p_{\theta }(x_{t-1}|x_t)$也服从类似的高斯分布:

上面的${\mu }_{\theta }$表示均值，${\Sigma }_{\theta }$表示对角协方差矩阵，整个工作即转换为对高斯分布的这两个参数的估计上。

均值估计：

对于均值的估计，通常情况下不采用直接匹配$p_{\theta }(x_{t-1}|x_t)$与$q(x_{t-1}|x_t,x_0)$之间的均值，而是通过估计当前时步添加的噪声${ϵ}_{\theta }$来实现。因为文中给出了均值和施加的球面高斯噪声之间的关系：

因此，将会训练一个神经网络${ϵ}_{\theta }$，以当前时步$x_t$为输入，估计前向过程添加的噪声$ϵ$，这部分的loss使用MSEloss：

一般的扩散模型对于协方差矩阵不做任何的约束和优化，而是假设其为给定的方差${\beta }_t$或者是前向过程中计算的${\tilde{\beta }}_t$，已经有研究证明${\beta }_t$与${\tilde{\beta }}_t$分别是反向过程中方差的上界与下界。不过，在时间片段比较短的情形下，只用这两个极端值作为协方差的估计并不准确，因此，本文使用了一个神经网络来生成权重$v$，使用$v$在上下界之间进行插值：

通常的扩散模型即以上面的$L_{simple}$为最终loss，而本文引用其他人的改进工作，使用$KL$散度约束预测分布$p_{\theta }(x0)$与真实分布$q(x0)$之间的变分下界：

最终的loss为：
$$Loss=L_{simple}+\lambda L_{vlb}$$
注意，$L_{simple}$只作用于均值的约束，不会影响协方差矩阵的约束，上述工作均不是本文的原创，而是综合其他人的工作所使用的架构。

4 模型架构

4.1 模型架构消融研究

本文使用的基础模型是其引文[24]中的UNet加一个单头全局注意力模块的架构。在此基础上探究了修改基础架构里不同组件对模型表现的影响，使用FID作为评价指标，在ImageNet 128×128上进行消融实现，设置batch size为256。

具体而言，主要评价了网络的宽度或者深度（保持模型总尺寸一致）；注意力头的数量；注意力的分辨率；使用BigGAN的残差模块进行UNet中的上采样和下采样激活；调整残差连接的权重等。

最后结果如表格1所示：

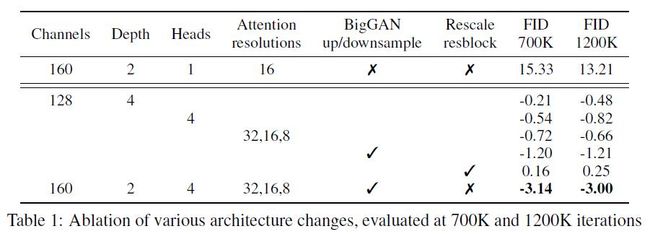
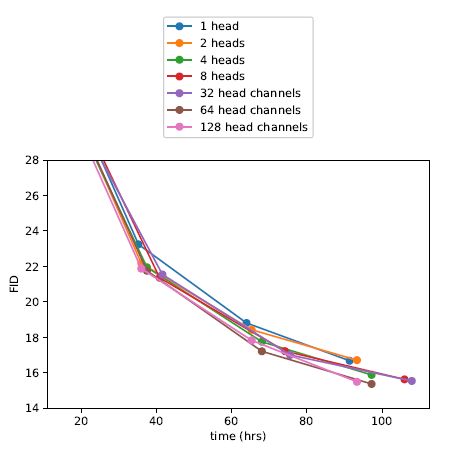
可以发现，加宽或者加深网络的深度都有助于提升模型表现，但报告的最好效果并未对其进行调整；同时，增加注意力头数，使用多分辨率组合的注意力模块比只使用单头单一分辨率更有助于提升模型表现，BigGAN的的上下采样残差块也有助于模型性能的提升，不过修改残差连接强度没有正面效果。与此同时，作者还证明使用通道数更小的注意力更有助于提升性能：

不过从右图中可以看出，注意力通道数为64时模型性能提升最快，所以后面都是用64作为注意力头的默认通道数。

此外，作者提出了一个自适应组归一化（Adaptive Group Normalization）的方法来进行归一化操作，这个方法是对组归一化的一个改进：
$$\text{AdaGN}(h,y=[y_s,y_b])=y_s\text{GroupNorm}(h)+y_b$$
上面公式中的$h$是残差块激活函数的输出，$y$是一个线性层对时步和后面用到的类别信息的嵌入。组归一化是对输入的通道方向进行分组归一化的归一化方法，可以理解为局部LayerNorm：

这里的消融实验做的比较少，只比较了他们的AdaGN和一个Baseline的效果：

4.2 类别信息指引

作者受目前高质量GAN网络通常使用类别信息辅助图像生成的原理启发，开发了一个将类别信息引入扩散模型进行图像生成的算法。该算法的思想是，使用不同时步的图像$x_t$训练一个分类器，之后使用分类器对$x_t$的梯度信息${\nabla }_{x_t}\text{log}{p}_{\theta }(x_t)$指导扩散模型的生成。

这个算法可以分成两块，一块是使用类别信息辅助模型进行噪声预测，来训练一个条件扩散模型；另一块是使用类别信息指导预训练的扩散模型进行采样。

噪声预测：

回到最开始的公式，每一个时步的数据都有两个关键参数，即高斯分布的均值和方差，而扩散模型主要是使用噪声估计代替直接进行均值估计：

作者通过公式推导，说明可以使用下面的公式替代上面的${ϵ}_{\theta }(x_t,t)$，给其引入类别条件：

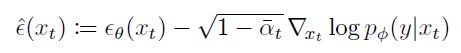
分类器指导：

分类器指导的思想与其进行噪声预测时的想法类似，主要是修改高斯分布的均值参数来指导图像按类别生成，有一个超参数$s$表示指导的程度，算法如下：

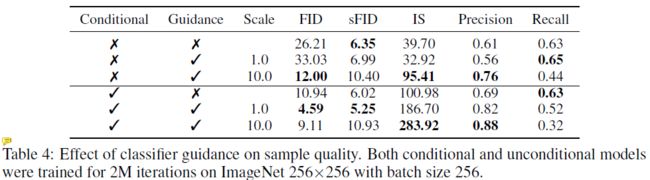
对于无条件的扩散模型，分类器梯度的指导提升了模型按类输出的性能（废话）：

模型质量也有提升：

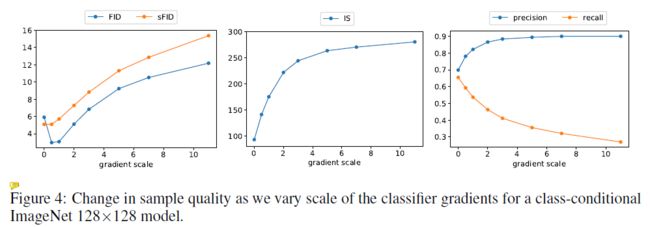
不过根据其对这一部分的消融实验的展示，好像上面的两个手段并没有一个直观的作用展示，不同指标在不同组合下达到最优值，而且加了分类器指导，调大强度，精度和IS提升了，FID和Recall下降了：

5 实验

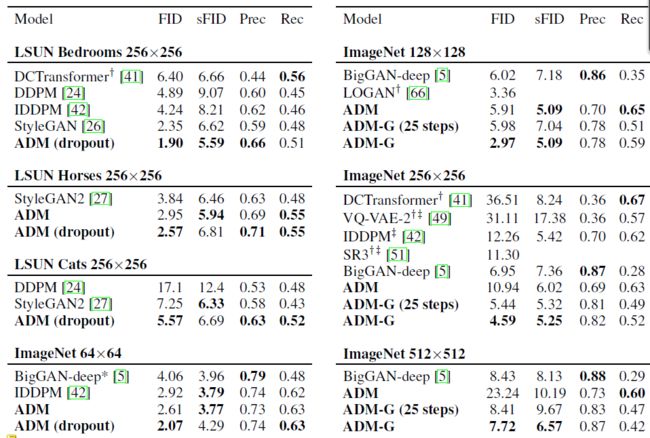
作者在ImageNet和LSUN数据集上进行了实验，评估了模型的FID、sFID（使用空间特征进行FID评估）、模型精度、召回率四个维度评估性能。发现他们的方法在ImageNet高分辨率的图像生成任务上全面超越了BigGAN-deep，不过模型精度有所欠缺。同时，在单类图像生成任务上，其FID都超过了StyleGAN2：

下面是定性的生成结果，左边是BigGAN-deep，中间是他们的ADM，右边是真实图像。