主成分分析R语言实现
主成分分析是一种常见的降维统计方法,它通过适当的变量替换,使得新变量成为原变量的线性组合,并且新变量间彼此独立,从而可从错综复杂的关系中寻求主要成分信息,揭示变量内在关系。本次主要分享的是该方法的R语言实现。
目录
-
-
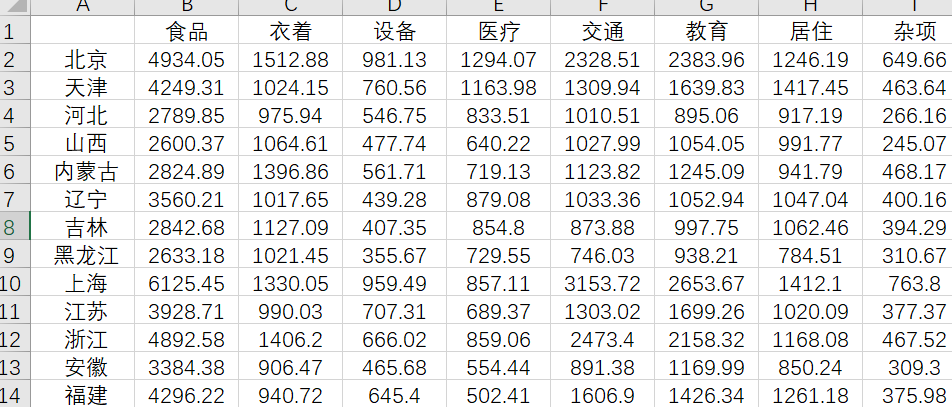
- 数据集展示
- 一、计算相关系数矩阵
- 二、确定主成分个数
- 三、主成分载荷分析
- 四、主成分得分
- 全部代码
-
数据集展示
一、计算相关系数矩阵
主成分分析法的前提是需要变量具有相关性,因此,我们需要先查看下各个变量的相关程度。
raw_data<-read.csv("data.csv",header=T)
new_data<-raw_data[,-1]
options(digits=2)
cor(new_data)

纵观整个相关系数矩阵,各个变量之间均存在一定的相关性,可进行后续的主成分分析
二、确定主成分个数
一般地,在计算相关系数矩阵后,通过求出其特征值与特征向量,进而计算方差贡献率与累计方差贡献率,这两步操作均可以由R中的princomp函数一步实现。
确定主成分准则:特征值大于1或累计方差贡献率大于80%(这个值具体需要根据主成分的个数与保留信息综合考虑确定)
PCA=princomp(new_data,cor=T)
summary(PCA)
screeplot(PCA,type="lines")


左侧为各主成分的标准差、方差贡献率、累计方差贡献率;右侧为碎石图,其为一种确定主成分的可视化图,将特征值从大到小排列,选择一个拐点对应的序号,此序号后的特征值全部较小且彼此相差不大,则该序号则可定位主成分的个数。(注意:各个主成分的方差与它对应的特征值是相等的!)
按照确定准则,左侧显示两个主成分即包含了原变量的84%的信息,而右侧的碎石图也显示出自第二个主成分后,其余主成分的特征值彼此差异不大。因此,最终确定为2个主成分。
三、主成分载荷分析
PCA$loadings[,1:2] #选择前两个主成分即可

从载荷矩阵来看,主成分Comp.1在设备、交通、教育、居住、杂项上载荷值较大,可视为非必须消费主成分;主成分Comp.2在食品、衣着、医疗上载荷值很大,可视为反映日常必须消费的主成分。
四、主成分得分
(一)计算综合得分
综合得分=各主成分的得分*各主成分方差/各主成分的方差和,在本次案例中,可将最终得分PC写为
P C = ( 2.38 8 2 ∗ C o m p . 1 + 1.101 4 2 ∗ C o m p . 2 ) / ( 2.38 8 2 + 1.101 4 2 ) PC=(2.388^2*Comp.1+1.1014^2*Comp.2)/(2.388^2+1.1014^2) PC=(2.3882∗Comp.1+1.10142∗Comp.2)/(2.3882+1.10142)
其中,Comp.1为主成分1的得分,Comp.2为主成分2的得分。现通过自编函数,进行综合得分的求解。
#m为主成分个数
caculate_score<-function(PCA,m){
comp_sd<-summary(PCA)$sdev[1:m] #各主成分标准差
comp_score_matrix<-PCA$scores[,1:m] #各主成分得分矩阵
comp_score<-data.frame(comp_score_matrix)
#计算综合得分
comp_score$PC<-as.numeric(comp_score_matrix%*%comp_sd^2/sum(comp_sd^2))
#计算排名
comp_score$rank<-rank(-comp_score$PC)
return(comp_score)
}
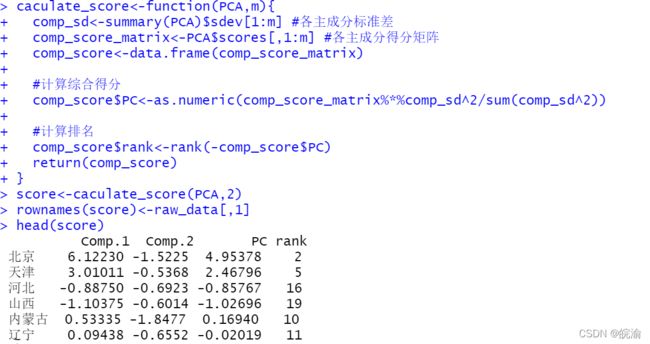
score<-caculate_score(PCA,2)
rownames(score)<-raw_data[,1]
head(score)
(二)主成分得分图分析
plot(score$Comp.1,score$Comp.2,
xlab='Comp.1',ylab='Comp.2',main='主成分得分图')
abline(h=0,lty=3);abline(v=0,lty=3)
text(score$Comp.1,score$Comp.2,rownames(score))

从得分图可知,在非必需消费主成分上comp.1得分最高的五个地区为上海、北京、广东、浙江、天津,且上海、北京的绝对值明显高于其他地区,表明在以设备、交通、教育、居住、杂项为主的非日常必需消费而言,上海、北京的消费水平远远高于其他省份。
在日常必需消费comp.2得分上,最高的五个地区为广东、海南、福建、广西、上海,可见这部分地区对于食品、衣着、医疗方面的消费较大。
全部代码
raw_data<-read.csv("data.csv",header=T)
new_data<-raw_data[,-1]
options(digits=2)
cor(new_data)
PCA=princomp(new_data,cor=T)
summary(PCA)
screeplot(PCA,type="lines")
#计算综合得分
caculate_score<-function(PCA,m){
comp_sd<-summary(PCA)$sdev[1:m] #各主成分标准差
comp_score_matrix<-PCA$scores[,1:m] #各主成分得分矩阵
comp_score<-data.frame(comp_score_matrix)
#计算综合得分
comp_score$PC<-as.numeric(comp_score_matrix%*%comp_sd^2/sum(comp_sd^2))
#计算排名
comp_score$rank<-rank(-comp_score$PC)
return(comp_score)
}
score<-caculate_score(PCA,2)
rownames(score)<-raw_data[,1]
head(score)
#绘制得分图
plot(score$Comp.1,score$Comp.2,
xlab='Comp.1',ylab='Comp.2',main='主成分得分图')
abline(h=0,lty=3);abline(v=0,lty=3)
text(score$Comp.1,score$Comp.2,rownames(score))
以上就是本次分享的全部内容~