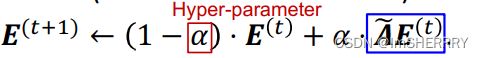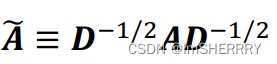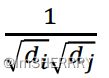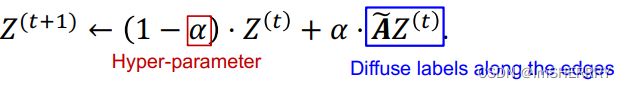CS224W 05-信息传递 message passing and node classification 学习笔记
目录
一、Relation Classification
二、Iterative Classification
三、Collective Classification:Correct & Smooth 矫正与光滑
1、Train Base Predictor
2、Predict over All Nodes
3、Post-Process Predictions
(1)Correct step 误差校正
(2)Smooth step 平滑标签
参考:
CS224W | Home (stanford.edu)
05-message.pdf (stanford.edu)
图机器学习——4.3 节点分类:Correct & Smooth (C&S)_Kanny广小隶的博客-CSDN博客
任务描述:
给定一张图,其中部分的节点已经有label,需要学习图的结构,将剩下未标注分类的节点进行标注——semi-supervised半监督的。
判断未知节点label的思想:
- homophily 同质性:拥有相似的节点属性->更可能有相同的label(节点自身的性质)
- influence 影响性:相同label的节点应该具有更强的连接/有边连接(学习图的结构)
三种经典方法:
一、Relation Classification
基本思想:节点v属于类c的概率Yv,是其邻居属于类c的概率 加权平均值。
1)对于已经有标签的节点,固定他们的Yv为真实标签 ground truth label Yv*
2)对于没有标签的节点,初始化Yv=0.5.(只是在这个0 1 分类的例子中,也可采用其他值)
3)用随机顺序(不一定要随机顺序,但实证上发现随机顺序效果最好,尤其对小图来说,这个更新的顺序会影响结果)更新所有无标签节点属于类c的概率,直至收敛/达到最大迭代数。
公式:
存在的问题:
- 不一定能收敛
- 模型没有考虑节点本身的属性/特征
计算的简单实例(来自hw1 第2题)
二、Iterative Classification
Relational Classification没有考虑节点的特征/属性,所以改进了方法,将考虑了节点属性和图结构的方法称为Iterative Classification。
基本思想:基于节点特征和邻居的标签对节点进行分类。
方法:
1)第一步——在训练集上训练两个分类器Classifier
(可以用线型分类器、神经网络等算法实现)
φ1(fv)基于节点特征的向量fv,预测节点标签。
φ2(fv,zv)基于fv和邻居节点标签的summary zv,预测节点标签
2)第二步——在测试集上迭代直至收敛
根据φ1预测标签,根据φ1计算出的标签计算zv,并用φ2预测标签,直至收敛或达到设定的最大迭代数(10/50/100……)
*模型不一定收敛。
*如何计算summary zv?zv是一个向量,可以是邻居标签的直方图(各标签的数目或比例)等等
计算的简单实例(来自hw1 第三题)网页分类
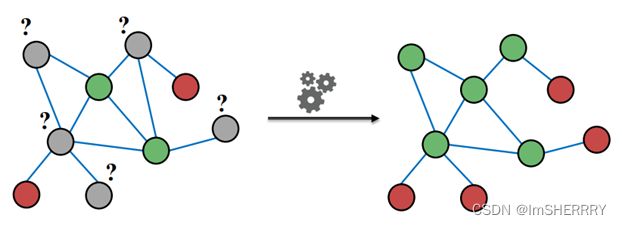
三、Collective Classification:Correct & Smooth 矫正与光滑
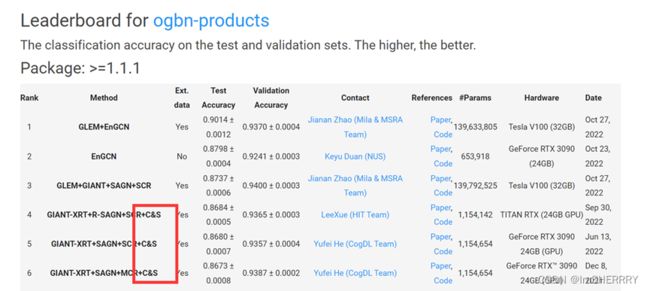
C&S是21年的state of art方法:Leaderboards for Node Property Prediction | Open Graph Benchmark (stanford.edu)
方法:
- 训练基本的predictor(基础浅层模型)
- 用训练得到的基本predictor预测所有节点的标签(soft labels 类别的概率)
- 考虑图结构,后处理所有的预测,得到节点的标签(矫正与光滑)
详细介绍:
1、Train Base Predictor
所有的节点都有特征信息,根据特征信息预测类别(不考虑图结构
预测得到的是soft labels(属于每个label的可能性)
已经有label的节点作为训练集/验证集
可以用linear model或MLP
2、Predict over All Nodes
用 1 中训练得到的预测机获得所有节点的soft labels
3、Post-Process Predictions
此时得到的预测结果没有用到图结构信息。
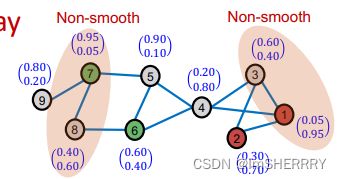
图具有同质性homophily,也就是边相连的两个节点,预测的误差应该是相似的(或者说正相关的)。该方法利用图的这种信息传递性来平滑节点的预测误差与标签。
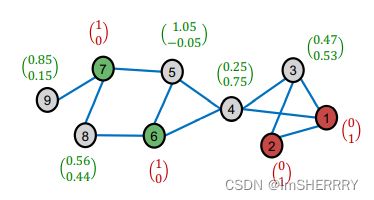
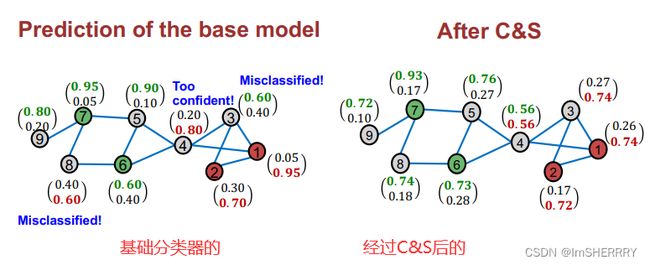
误差校正的目的是 让某一些节点误差比较大的(概率趋向于0.5? 比如图中的节点8)更加精准的预测
平滑标签的目的是让相邻的两个节点之间的预测概率尽量不要有太大的差异
(1)Correct step 误差校正
计算每个节点的训练误差,没有标签的节点初始误差记为0。
初始误差为:
按照图的结构,构建误差传播网络。迭代公式定义如下:
α是超参数,控制保留多少比例上一步的信息(和PageRank类似),通过标准化的邻接矩阵![]() 传递多少信息。信息在这里指误差。
传递多少信息。信息在这里指误差。![]() 的定义如下:
的定义如下:
D=diag(d1,d2,…,dN)为度矩阵(对角线存放每个节点的度)
不直接使用邻接矩阵A,而是考虑标准化的邻接矩阵,其目的是:考虑邻居节点多的节点倾向于有更大的影响力,从而不让度大的节点对本节点影响力过大。
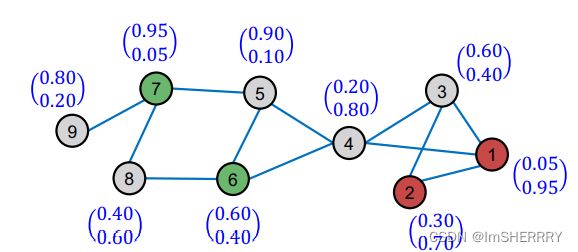
将α设定为0.8,在三轮迭代传播后,每个节点的误差如下:
而后在预测的软标签中加入经过缩放尺度s ss缩放的扩散后的训练误差,得到我们第二步误差矫正的结果。
(2)Smooth step 平滑标签
通过图结构,传递已标注节点 正确的软标签(基于邻居节点倾向于有相同的标签)
用真实的标签替代上一步预测的(对于有标签的节点)
迭代公式和上一步误差校正类似:
将α设置为0.8,迭代三次后结果如下:
由于节点两个值加起来不为1,因此选择较大的值为最终的类别。
结果比较: